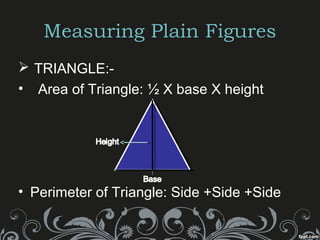
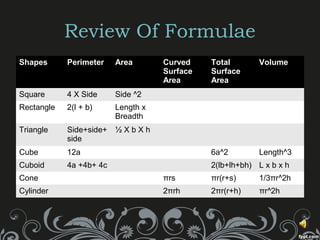
This document provides information about mensuration, which is the measurement of geometric figures. It begins with acknowledging the teacher for providing the opportunity to present on this topic. It then defines important terms like perimeter, area, volume, and introduces plain and solid figures. Formulas for calculating the perimeter, area, surface area and volume of squares, rectangles, triangles, cubes, cuboids, cylinders and cones are presented along with examples. The document concludes by listing the group members who prepared the presentation.

1. MENSURATION

2. Acknowledgement
We would like to express our special thanks to our Math's
teacher who gave us the golden opportunity to do this
wonderful presentation on the topic ‘Mensuration’. This
helped us in doing a lot of research work and we came to
know about many things, I am really grateful to the
teacher for her constant guidance and support.

3. Contents
Introduction
Quote—Unquote
Important Terms
Figures
Measuring Plain Figures
Measuring Solid Figures
Review Of Formulae
Group Members

4. INTRODUCTION
• Mensuration is the branch of geometry which deals with
the measurement of area, length or volume. It is also the
act or process of measuring.
• The Mensuration took its birth in Egypt.
Then it was applied and expanded by great people like
Pythagoras, Euclid, Archimedes, Ptolemy etc and
further developed by Halley, Bernouillies, Euler, Newton
etc.

6. Quote--Unquote
 Listen to some famous quotes from
famous people about geometry.
 I think the universe is pure geometry-
basically, a beautiful shape twisting
around space-time.
 There is geometry in the humming of
strings, there is music in the spacing of
spheres.

7. Important Terms
• Solid: A body or geometric figure having three
dimensions.

8. Important Terms
• Surface Area: The total area of the surface of the three
dimensional figure.

9. Important Terms
• Perimeter: The continuous line forming the boundary of a
geometrical figure.

10. Important Terms
• Volume: The total space occupied by an object or the space
inside a container.

11. Figures
• Plain figures: Plain figures are all about flat 2-
dimensional shapes such as circle, rectangle, etc.
• Solid Figures: Solid Geometry consists of all 3-
dimensional figures like cubes, spheres, etc.

12. Measuring Plain Figures
 SQUARE :-
• Perimeter of Square: 4 X Side
SIDE
All sides are equal in a
square, therefore
No. of sides= 4
Perimeter= Side X 4
Area of Square: Side X Side

13. Measuring Plain Figures
 TRIANGLE:-
• Area of Triangle: ½ X base X height
• Perimeter of Triangle: Side +Side +Side

14. Measuring Plain Figures
 RECTANGLE:-
• Perimeter of Rectangle: 2(length +
breadth)
Opposite sides are equal, hence
» Perimeter= Length+ breadth+
» length+ breadth
» = 2 (length + breadth)

15. Measuring Solid Figures
 CUBE:-
• Surface Area of Cube: 6 a^2
Number of Faces=6
Area of each face= Side X Side
= a X a
= a^2
Total Area= 6 a^2

16. • Volume of Cube: Length^3
Volume= Length X Breadth X Height
As the length, breadth and height are
all equal hence
Volume= Length^3

17. Example
 Let a cube have a side measuring 2 cm.
Find its area as well as volume.
 Side=2 cm
Surface area= 6a^2
= 6(2 X 2)
= 6 X 4
Surface Area= 24 cm^2
2cm
2 cm

18. Example (Contd.)
Volume= length^3
Length= 2cm
Volume= 2 X 2 X 2
= 8 cm^3

19.  CUBOID:-
• Surface Area of Cuboid: 2(lb + bh + lh)
Number of Rectangle=6
Area of each rectangle=
length X breadth + length X breadth +
length X height + length X height +
breadth X height + breadth X height
Total Surface Area= 2 (lb + bh + lh)

20. • Volume of Cuboid= length X breadth X
height

21. Example
 Let the dimensions of a cuboid be as
follows- l=1 cm, b=2 cm, h=3 cm. Find the
total surface area and volume.
 Surface Area=2(lb+bh+lh)
= 2(1X2 + 2X3 + 1X3)
= 2(2 + 6 + 3)
= 2(11)
= 22 cm^2
1 cm
3cm
2
cm

22. Example (Contd.)
Volume= length X breadth X height
= 1 X 2 X 3
= 6 cm^3

23.  Cylinder:-
• Curved Surface Area: 2πrh
When we cut this cylinder along the height
then it will form a rectangle with
dimensions: 2πr and h. This is the
area of
» the curved surface.
» 2πr because, the breadth of the
rectangle= circumference of base’s circle.
r
h
2πr
h

24. • Total Surface Area: 2πr(r+h)
Total Surface Area = Area of 2 circles
+ Curved Surface Area
TSA= πr^2 + πr^2 + 2πrh
TSA= 2πr^2 + 2πrh
Total Surface Area = 2πr(r+h)
• Volume: πr^2h
r
h

25. Example
 Let a cylinder have radius=2 cm and
height= 7 cm. Find the TSA, CSA and
volume of the same.
 Radius=2 cm
Height= 7 cm
CSA= 2πrh
= 2 X 22/7 X 2 X 7
= 88 cm^2
7cm
2 cm

26. Example (Contd.)
TSA= 2πr(r+h)
= 2 X 22/7 X 2(2+7)
= 2 X 22/7 X 18
= 113.14 cm^2
Volume= πr^2h
= 22/7 X (2)^2 X 7
= 22/7 X 4 X 7
= 88 cm^3

27.  CONE:
• Curved Surface Area: πrs
Radius= r
Slant Height= s
(Cut it along the radius and slant height.)
Area of ABC/ Area of circle with centre C=
Arc length of AB of sector ABC/
Circumference of circle with centre C
Area of ABC/πs^2 = 2πr/2πs = r/s ,
Area of sector ABC = r/s X πs^2
Curved Surface Area = πrs
r
s
A B
C
s

28. • Total Surface Area:
= Area of Base + Area of curved surface
= πr^2 + πrs
= πr(r+s)
• Volume: 1/3 πr^2h

29. Example
 Let the radius of the cone be 7 cm and
the slant height be 2 cm. Find it’s CSA,
TSA and volume.
 CSA= πrs
= 22/7 X 7 X 2
= 44 cm^2
TSA= πr(r+s)
= 22/7 X 7(7+2)
7
2

30. Example (Contd.)
= 22/7 X 7 X 9
= 198 cm^2
Volume= 1/3 πr^2h
= 1/3 X 22/7 X 49 X 2
= 1/3 X 22 X 14
= 1/3 X 308
= 102.66 cm^3

31. Review Of Formulae
Shapes Perimeter Area Curved
Surface
Area
Total
Surface
Area
Volume
Square 4 X Side Side ^2
Rectangle 2(l + b) Length x
Breadth
Triangle Side+side+
side
½ X b X h
Cube 12a 6a^2 Length^3
Cuboid 4a +4b+ 4c 2(lb+lh+bh) L x b x h
Cone πrs πr(r+s) 1/3πr^2h
Cylinder 2πrh 2πr(r+h) πr^2h

32. Group Members
 Karan Singh Bora
 Amaan Ahmad
 Vasu Arora
 Tushar Sabhani
 Utsav Garg