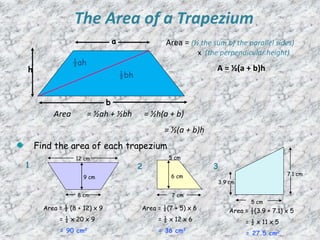
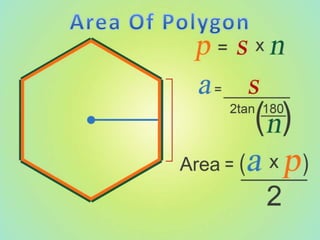
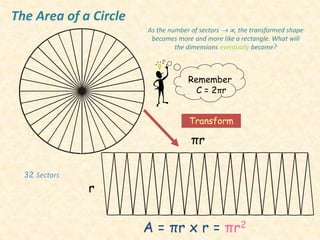
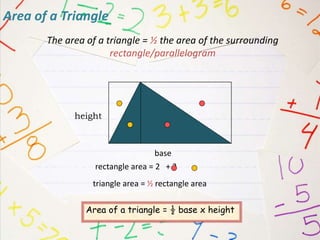
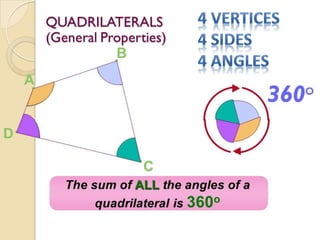
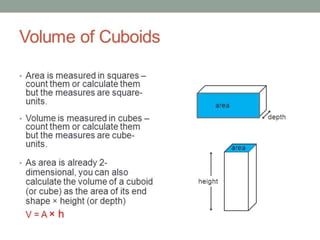
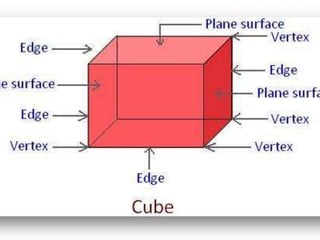
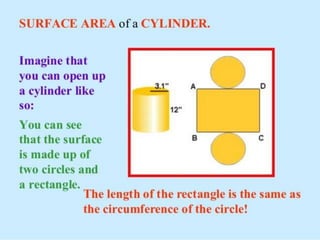
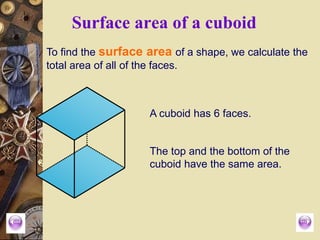
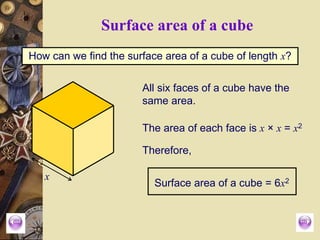
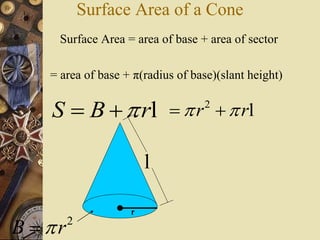
The document outlines formulas for calculating the areas of various geometrical shapes, including trapeziums, circles, triangles, cubes, cuboids, and cones. It provides specific examples and calculations for each shape's area and discusses surface area concepts. Additionally, it briefly addresses the volume of solids and surface area calculations.

4. The Area of a Trapezium
Area = (½ the sum of the parallel sides)
x (the perpendicular height)
A = ½(a + b)h
a
b
h
½ah
½bh
Area = ½ah + ½bh = ½h(a + b)
= ½(a + b)h
Find the area of each trapezium
1
8 cm
12 cm
9 cm
2
5 cm
7 cm
6 cm
3
5 cm
3.9 cm
7.1 cm
Area = ½ (8 + 12) x 9
= ½ x 20 x 9
= 90 cm2
Area = ½(7 + 5) x 6
= ½ x 12 x 6
= 36 cm2
Area = ½(3.9 + 7.1) x 5
= ½ x 11 x 5
= 27.5 cm2

6. 32 Sectors
Transform
Remember
C = 2πr
?
?
As the number of sectors  , the transformed shape
becomes more and more like a rectangle. What will
the dimensions eventually become?
½C
r
πr
A = πr x r = πr2
The Area of a Circle

7. Find the area of the following circles. A = r2
8 cm
1
10 cm
2
Examples

8. Area of a Triangle
rectangle area = 2 + 2
triangle area = ½ rectangle area
base
height
Area of a triangle = ½ base x height
The area of a triangle = ½ the area of the surrounding
rectangle/parallelogram

10. What is volume?
The volume of a solid, cube or cuboid
refers to the capacity of the
solid or the amount of space
inside the solid.

17. To find the surface area of a shape, we calculate the
total area of all of the faces.
A cuboid has 6 faces.
The top and the bottom of the
cuboid have the same area.
Surface area of a cuboid

18. How can we find the surface area of a cube of length x?
Surface area of a cube
x
All six faces of a cube have the
same area.
The area of each face is x × x = x2
Therefore,
Surface area of a cube = 6x2

19. Surface Area of a Cone
Surface Area = area of base + area of sector
= area of base + π(radius of base)(slant height)
S B r  l 2
r r   l
l
2
B r
r

20. Acknowledgement