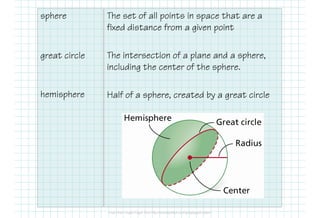
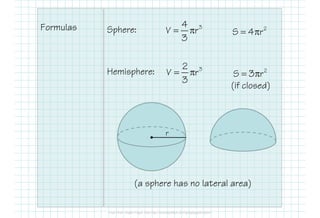
This document provides information about calculating the surface area and volume of spheres, hemispheres, and composite figures. It defines spheres, hemispheres, and great circles. Formulas are provided for calculating the surface area and volume of spheres and hemispheres. Examples show how to use the formulas to find the surface area and volume of spheres and hemispheres given specific measurements. The document notes that composite figures can be broken down into simpler shapes to calculate their total surface area and volume by combining the surface areas and volumes of each individual shape. An example demonstrates this process for a composite prism and cylinder figure.

1. 5.13.6 Spheres & Composite Figures
The student is able to (I can):
• Find the surface area and volume of spheres and
hemispheres
• Find the surface area and volume of composite figures

2. sphere
great circle
hemisphere
The set of all points in space that are a
fixed distance from a given point
The intersection of a plane and a sphere,
including the center of the sphere.
Half of a sphere, created by a great circle

3. Formulas Sphere:
Hemisphere:
(a sphere has no lateral area)
= π 34
V r
3
r
= π 2
S 4 r
= π 32
V r
3
= π 2
S 3 r
(if closed)

4. Examples Find the surface area and volume:
1. A sphere with radius 9 m.
2. A closed hemisphere with radius 12 ft.
( )2 2
S 4 9 324 m= π = π
( )3 34
V 9 972 m
3
= π = π
( )2 2 21
S 4 r r 3 r
2
= π + π = π
( )2 2
3 12 432 ft= π = π
( )3 32
V 12 1152 ft
3
= π = π

5. 3. A sphere with diameter 20 in.
r = 10 in.
4. What is the radius of a sphere whose
volume is 7776π cubic feet.
( )2 2
S 4 10 400 in= π = π
( )3 34 4000
V 10 in
3 3
= π = π
34
r 7776
3
π = π
( )3 3
r 7776 5832
4
 = = 
 
3
r 5832 18 ft.= =

6. Much like composite plane figures, to find
the surface area and volume of composite
shapes, break it down into simpler shapes
and combine.
While volume is a fairly straightfoward
process, when you calculate the surface
area of a composite shape, you need to
take into account portions of the shape
that might be covered up by other shapes.

7. Example Find the volume and surface area of the
shape below.
Volume: total prism cylinderV V V= +
( )( )( ) ( )( )2
9 4 5 2 3= + π
3
180 12 217.7 cm= + π ≈

8. Example Find the volume and surface area of the
shape below.
Surface Area:
total prism cylS S L= +
( ) ( ) ( )[ ] ( )( )prismS 5 2 9 2 4 2 9 4
202
= + +
=
( )( )cylL 2 2 3
12
= π
= π
2
totalS 202 12 239.7 cm= + π ≈
We only need lateral area
because the one visible base
of the cylinder offsets the
missing circle on the prism.