Dokumen ini membahas geometri analitik ruang, khususnya tentang persamaan bidang rata dan sudut antara dua bidang. Penjelasan mencakup cara menentukan besar sudut antara dua bidang menggunakan vektor normal, juga memberikan contoh soal mengenai kedudukan sejajar dan tegak lurus antara dua bidang. Selain itu, dokumen ini menjelaskan cara menghitung jarak antara titik dan bidang serta antar dua bidang sejajar.

1. 3 November 2014
Geometri Analitik
Ruang

2. S u d u t A n t a r a D u a B i d a n g
R a t a
Persamaan umum dari suatu bidang rata : 𝑽 = 𝑨𝒙 + 𝑩𝒚 + 𝑪𝒛 + 𝑫 = 𝟎
Vektor normalnya : 𝒏 = [𝑨, 𝑩, 𝑪]
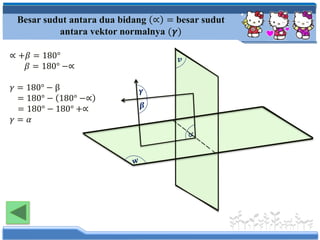
Sudut antara dua bidang rata merupakan sudut antara vektor-vektor
normalnya. Gambar
Misalnya, sudut antara bidang: 𝑉1 = 𝐴1 𝑥 + 𝐵1 𝑦 + 𝐶1 𝑧 + 𝐷1 = 0 dan 𝑉2 =
𝐴2 𝑥 + 𝐵2 𝑦 + 𝐶2 𝑧 + 𝐷2 = 0 maka sudutnya adalah sudut antara vektor-
vektor normalnya, 𝑛1= [𝐴1, 𝐵1, 𝐶1] dan 𝑛2 = [𝐴2, 𝐵2, 𝐶2] yaitu:
cos θ =
𝑛1 ∙ 𝑛2
𝑛1 𝑛2
=
𝐴1 𝐴2 + 𝐵1 𝐵2 + 𝐶1 𝐶2
𝐴1
2
+ 𝐵1
2
+ 𝐶1
2
∙ 𝐴2
2
+ 𝐵2
2
+ 𝐶2
2

3. S u d u t A n t a r a D u a B i d a n g
R a t aContoh :
Tentukan besar sudut antara 𝑥 + 𝑦 + 𝑧 + 3 = 0 dan 2𝑥 + 𝑦 + 2𝑧 – 11 = 0 !
Penyelesaian : cos 𝜃 =
𝐴1 𝐴2+𝐵1 𝐵2 + 𝐶1 𝐶2
𝐴1
2
+𝐵1
2+𝐶1
2
. 𝐴2
2
+𝐵2
2+𝐶2
2
cos 𝜃 =
1(2) + 1(1) + 1(2)
12 + 12 + 12 . 22 + 12 + 22
cos 𝜃 =
5
3 . 9
cos 𝜃 =
5
3 3
𝜃 = 𝑎𝑟𝑐𝑐𝑜𝑠 0,962
𝜃 ≈ 15, 79°

4. K E D U D U K A N 2 B U A H
B I D A N G R A T A
1. Kedudukan sejajar
Bila 𝑉1 dan 𝑉2 sejajar maka 𝑛1dan 𝑛2 sama (atau berkelipatan),
berarti [𝐴1, 𝐵1, 𝐶1] = 𝜆 [𝐴2, 𝐵2, 𝐶2] adalah syarat bidang 𝑉1 dan
𝑉2 sejajar (𝜆 sebarang ≠ 0).
𝑉1 ⫽ 𝑉2 ⟺ 𝑛𝑉1 ⫽ 𝑛𝑉2 → 𝑛𝑉1 = 𝑘𝑛𝑉2 ( 𝑘 bilangan riil)
→ 𝐴1, 𝐵1, 𝐶1 = 𝑘 𝐴2, 𝐵2, 𝐶2
→ 𝑘 =
𝐴1
𝐴2
=
𝐵1
𝐵2
=
𝐶1
𝐶2

5. K E D U D U K A N 2 B U A H
B I D A N G R A T A
2. Kedudukan tegak lurus
Bila 𝑉1 tegak lurus 𝑉2, maka vektor normalnya akan saling tegak
lurus, 𝑛1 ⊥ 𝑛2, atau 𝑛1 . 𝑛2 = 0 → 𝐴1 𝐴2 + 𝐵1 𝐵2 + 𝐶1 𝐶2 = 0
𝑉1 ⊥ 𝑉2 ⟺ 𝑛𝑉1 ⊥ 𝑛𝑉2 → 𝑛𝑉1 ∙ 𝑛𝑉2 = 0
→ 𝐴1, 𝐵1, 𝐶1 ∙ 𝐴2, 𝐵2, 𝐶2 = 0
→ 𝐴1 𝐴2 + 𝐵1 𝐵2 + 𝐶1 𝐶2 = 0

6. K E D U D U K A N 2 B U A H
B I D A N G R A T AContoh 1
Tentukan persamaan bidang rata 𝑉2 jika diketahui 𝑉2 melalui titik (0,2,1) yang
sejajar dengan bidang rata 𝑉1 = 𝑥 + 𝑦 + 5𝑧 = 9.
Penyelesaian :
𝑉1 = 𝑥 + 𝑦 + 5𝑧 = 9, karena 𝑉1 sejajar 𝑉2 maka 𝑛1 = 𝑛2,
𝑛1 = [1,1,5] maka 𝑉2 akan berbentuk 𝑥 + 𝑦 + 5𝑧 + 𝐷2 = 0.
Sehingga bidang rata 𝑉2 yang melalui titik (0,2,1) menjadi:
𝑉2 = 𝑥 + 𝑦 + 5𝑧 + 𝐷2 = 0
0 + 2 + 5(1) + 𝐷2 = 0
7 + 𝐷2 = 0
𝐷2 = −7
Jadi, persamaan 𝑉2 = 𝑥 + 𝑦 + 5𝑧 − 7 = 0

7. K E D U D U K A N 2 B U A H
B I D A N G R A T AContoh 2
Tentukan persamaan bidang rata 𝑉2 yang tegak lurus pada bidang rata 𝑉1 ≡
𝑥 + 𝑦 + 𝑧 = 1 serta melalui titik (0,0,0) dan (1,1,0).
Penyelesaian:
Misalkan 𝑉2 ∶ 𝐴2 𝑥 + 𝐵2 𝑦 + 𝐶2 𝑧 + 𝐷2 = 0, tegak lurus 𝑉1 berarti:
𝐴1 𝐴2 + 𝐵1 𝐵2 + 𝐶1 𝐶2 = 0 atau
𝐴2 + 𝐵2 + 𝐶2 = 0
𝐶2 = − 𝐴2 − 𝐵2…...............................................................(*)
𝑉2 melalui titik (0,0,0) berarti: 𝐷2 = 0, dan melalui titik (1,1,0) berarti: 𝐴2 +
𝐵2 = 0 atau
𝐴2 = −𝐵2...............................................................................................(**)
Substitusikan persamaan (**) 𝐶2ke (*)
𝐶2 = − 𝐴2 − 𝐵2
𝐶2 = − − 𝐵2 − 𝐵2
𝐶2 = 0
Jadi persamaan 𝑉2 ∶ −𝐵2 𝑥 + 𝐵2 𝑦 + 0𝑧 + 0 = 0 atau – 𝑥 + 𝑦 = 0

8. Jarak antara sebuah titik & sebuah
bidang rata & jarak antara dua bidang
sejajarMisalkan, 𝑝 = jarak titik (0,0,0) ke bidang
𝑉1 = 0, dimana p ≥ 0 dan R (𝑥, 𝑦, 𝑧) titik
sebarang pada bidang, maka dapat ditulis:
xcos ∝ + 𝑦cos𝛽 + 𝑧cos𝛾 = 𝑝
yang disebut persamaan normal (HESSE)
dari bidang 𝑉1 = 0. Kita hendak
menentukkan jarak titik 𝑅(𝑥1, 𝑦1, 𝑧1) ke
bidang 𝑉1. Kita buat bidang 𝑉2 melalui 𝑅
yang sejajar 𝑉1. Jadi, vektor normal 𝑉1 dan
𝑉2 sama.

9. Jarak antara sebuah titik & sebuah
bidang rata & jarak antara dua bidang
sejajarSedangkan jarak titik asal 0 ke 𝑉2adalah 𝑝 ±
𝑑 (tergantung letak 𝑉1 dan 𝑉2 terhadap titik
0).
𝑉2 = 𝑥𝑐𝑜𝑠𝛼 + 𝑦𝑐𝑜𝑠𝛽 + 𝑧𝑐𝑜𝑠𝛾 = 𝑝 ± 𝑑, dan
karena 𝑅(𝑥1, 𝑦1, 𝑧1) pada 𝑉2, maka terpenuhi
𝑥1 𝑐𝑜𝑠𝛼 + 𝑦1 𝑐𝑜𝑠𝛽 + 𝑧1 𝑐𝑜𝑠𝛾 = 𝑝 ± 𝑑 atau
𝑑 = | 𝑥1 𝑐𝑜𝑠𝛼 + 𝑦1 𝑐𝑜𝑠𝛽 + 𝑧1 𝑐𝑜𝑠𝛾 − 𝑝|
adalah jarak titik 𝑅(𝑥1, 𝑦1, 𝑧1) ke bidang 𝑉1 =
𝑥𝑐𝑜𝑠𝛼 + 𝑦𝑐𝑜𝑠𝛽 + 𝑧𝑐𝑜𝑠 𝛾 = 𝑝. Kalau 𝑉1
berbentuk 𝐴𝑥 + 𝐵𝑦 + 𝐶𝑧 + 𝐷 = 0
maka :
𝑑 =
𝐴𝑥1 + 𝐵𝑦1 + 𝐶𝑧1 + 𝐷
𝐴2 + 𝐵2 + 𝐶2

10. Jarak antara sebuah titik & sebuah
bidang rata & jarak antara dua bidang
sejajarUntuk mencari jarak dua bidang sejajar 𝑉2, kita ambil sembarang titik pada
𝑉2, lalu menghitung jarak titik tersebut ke 𝑉1.
Contoh:
1. Tentukan jarak titik (4,7,3) ke bidang 2𝑥 + 6𝑦 – 3𝑧 = 13.
Penyelesaian:
𝑑 =
2 . 4 + 6 . 7 + −3 . 3 − 13
22 + 62 + (−3)2
𝑑 =
8 + 42 − 9 − 13
4 + 36 + 9
𝑑 =
28
49
𝑑 =
28
7
𝑑 = 4

11. Jarak antara sebuah titik & sebuah
bidang rata & jarak antara dua bidang
sejajar2. Diketahui 𝑉1 = 𝑥 + 𝑦 + 𝑧 – 2 = 0 dan 𝑉2 = 𝑥 + 𝑦 + 𝑧 – 5 = 0.
Jika 𝑅 pada 𝑉2, hitunglah jarak tersebut ke 𝑉1.
Penyelesaian :
Misal, kita pilih R pada 𝑉2 misalnya, 𝑥 = 0, 𝑦 = 0 dan 𝑧 = 5, didapat
𝑅 (0,0,5). Maka jarak titik 𝑅 ke 𝑉1 adalah
𝑑 =
1 .0 + 1 .0 + 1 . 5−2
12+ 12 + 12
𝑑 =
3
3
𝑑 = 3

12. Thank’s for your
attention

13. 𝒗
Besar sudut antara dua bidang ∝ = besar sudut
antara vektor normalnya (𝜸)
∝ +𝛽 = 180°
𝛽 = 180° −∝
𝛾 = 180° − β
= 180° − 180° −∝
= 180° − 180° +∝
𝛾 = 𝛼