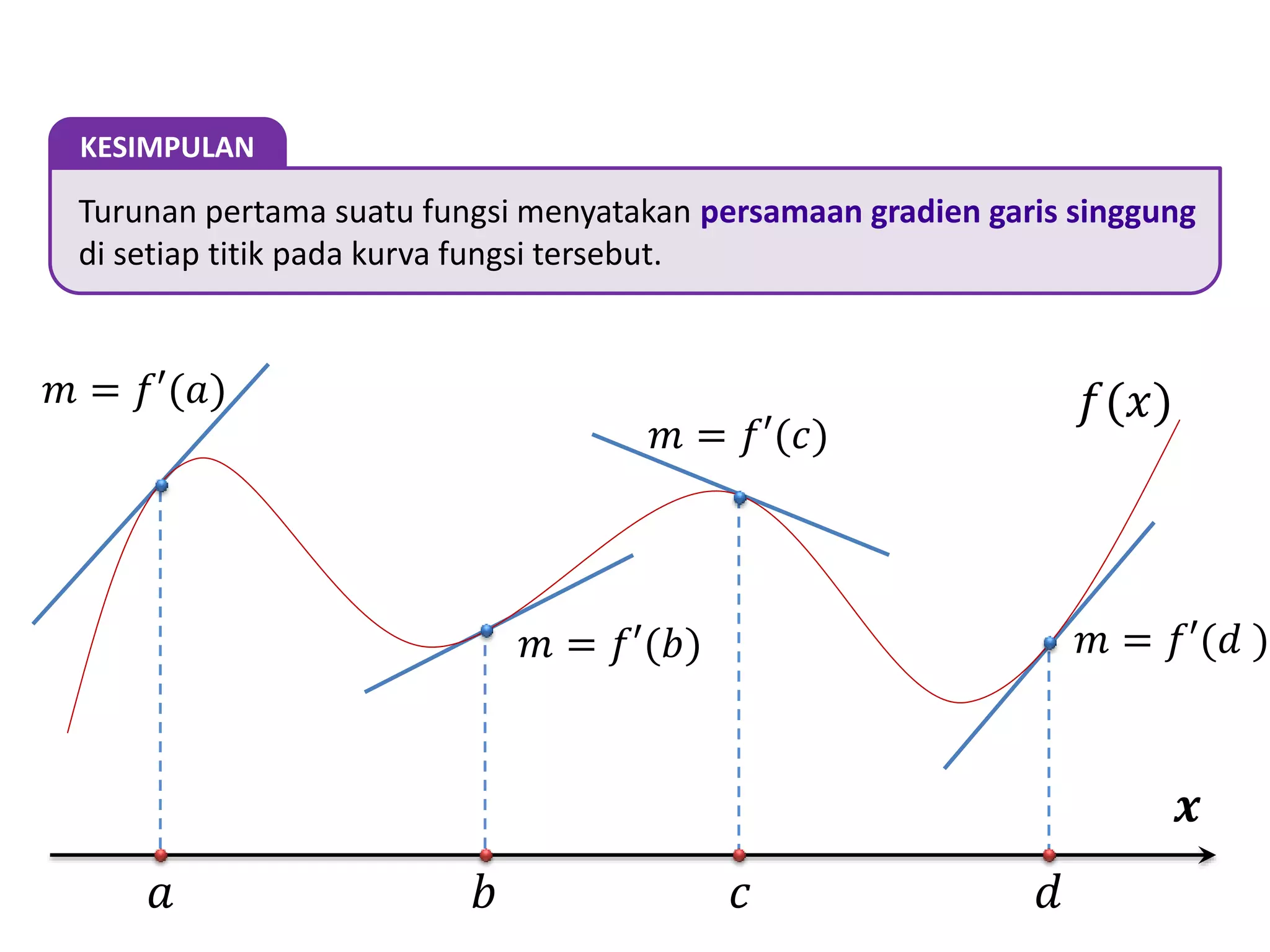
Turunan fungsi menyatakan gradien garis singgung pada setiap titik kurva fungsi. Turunan berguna untuk menentukan naik turunnya fungsi, nilai maksimum atau minimum, serta gradien fungsi. Pembelajaran turunan meliputi rumus turunan, sifat-sifat turunan, dan penentuan nilai turunan.