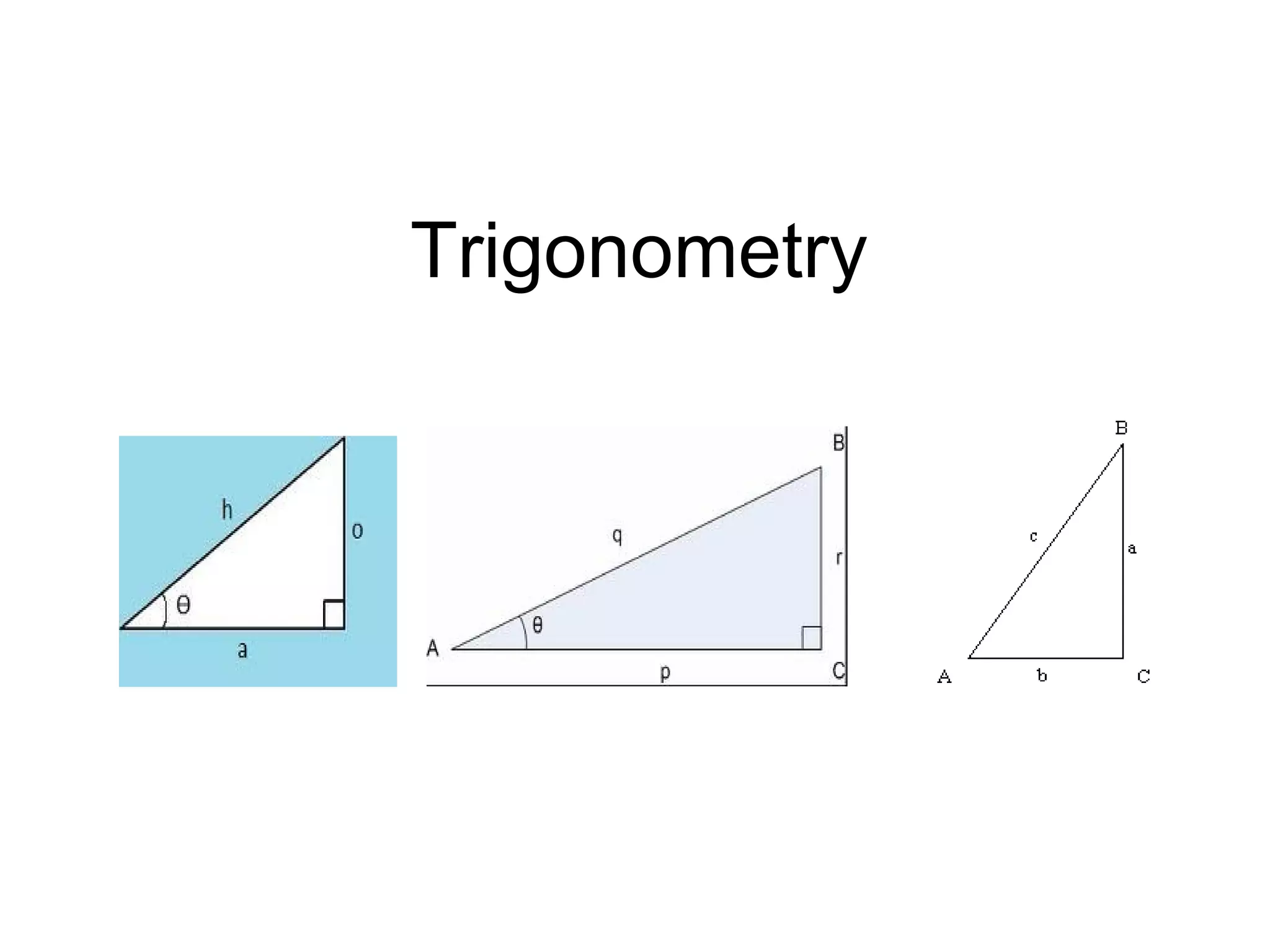
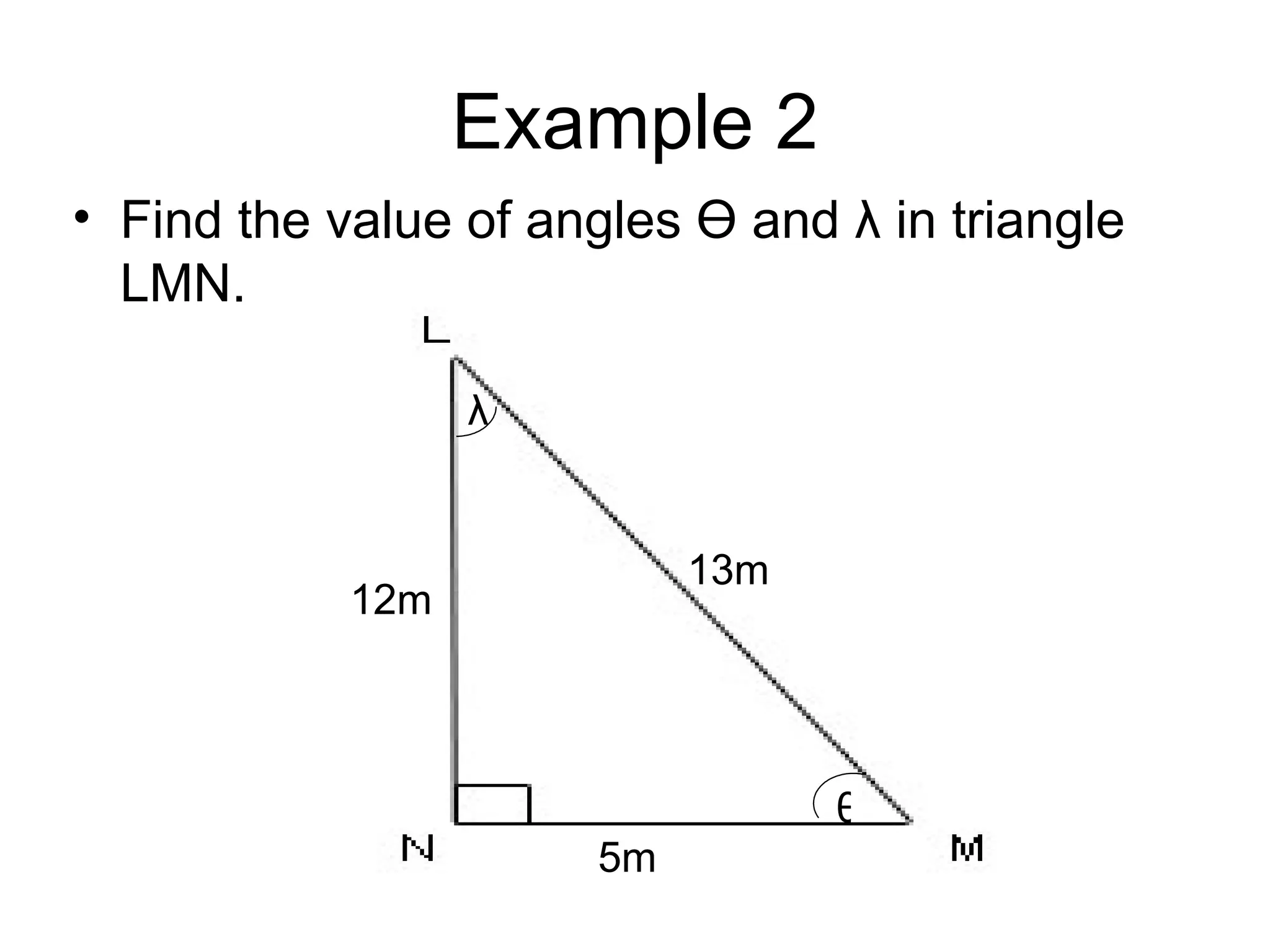
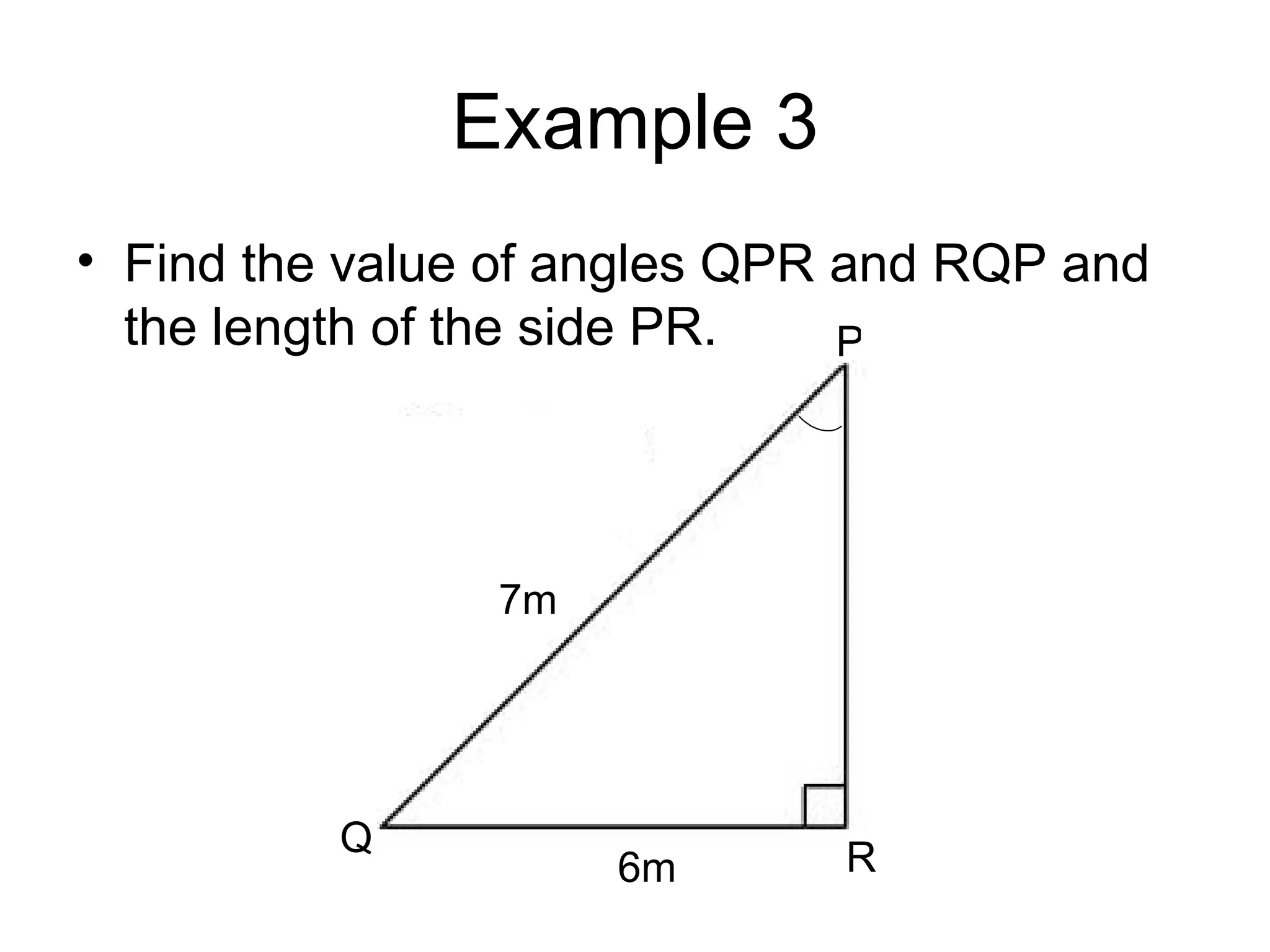
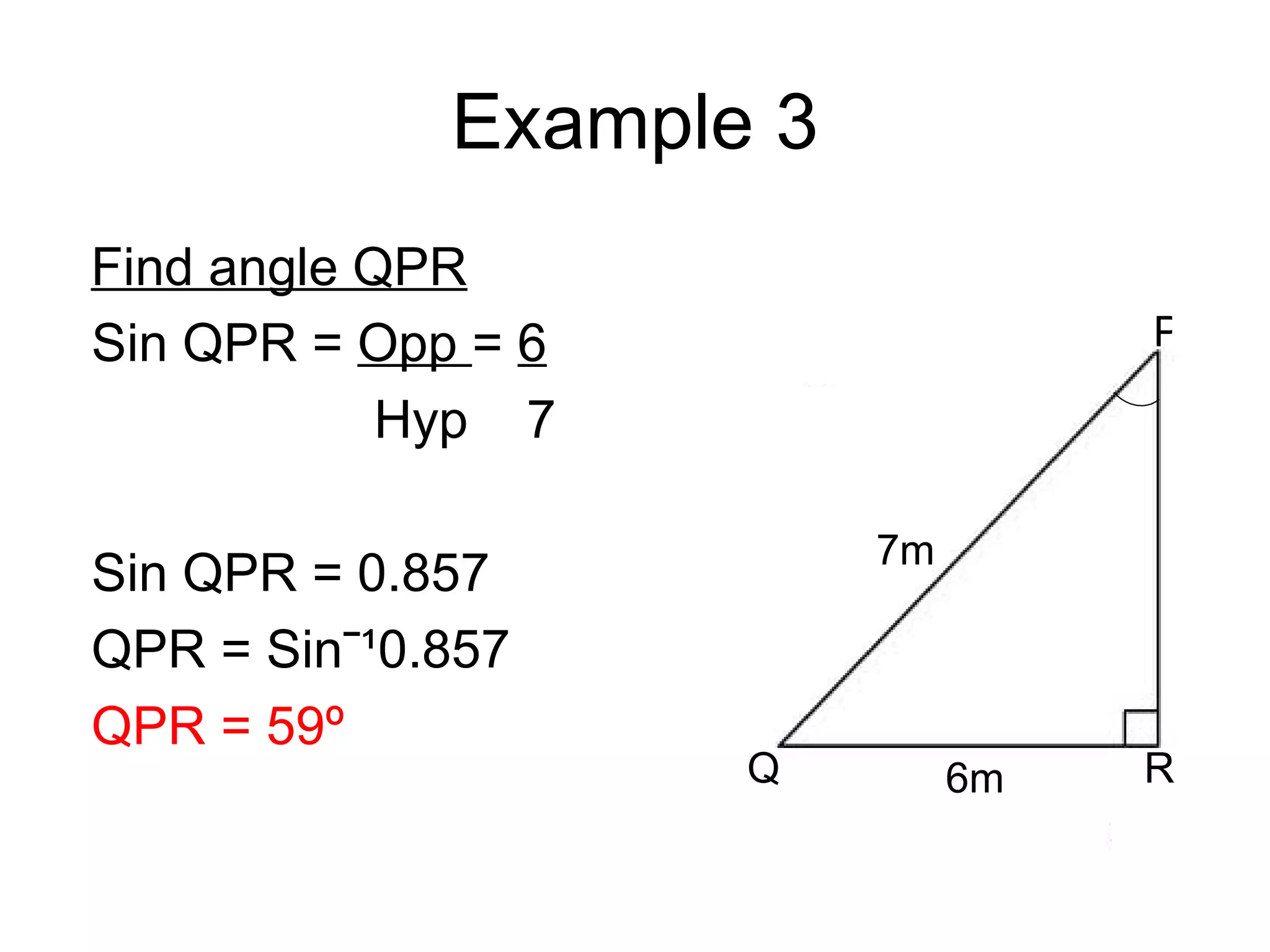
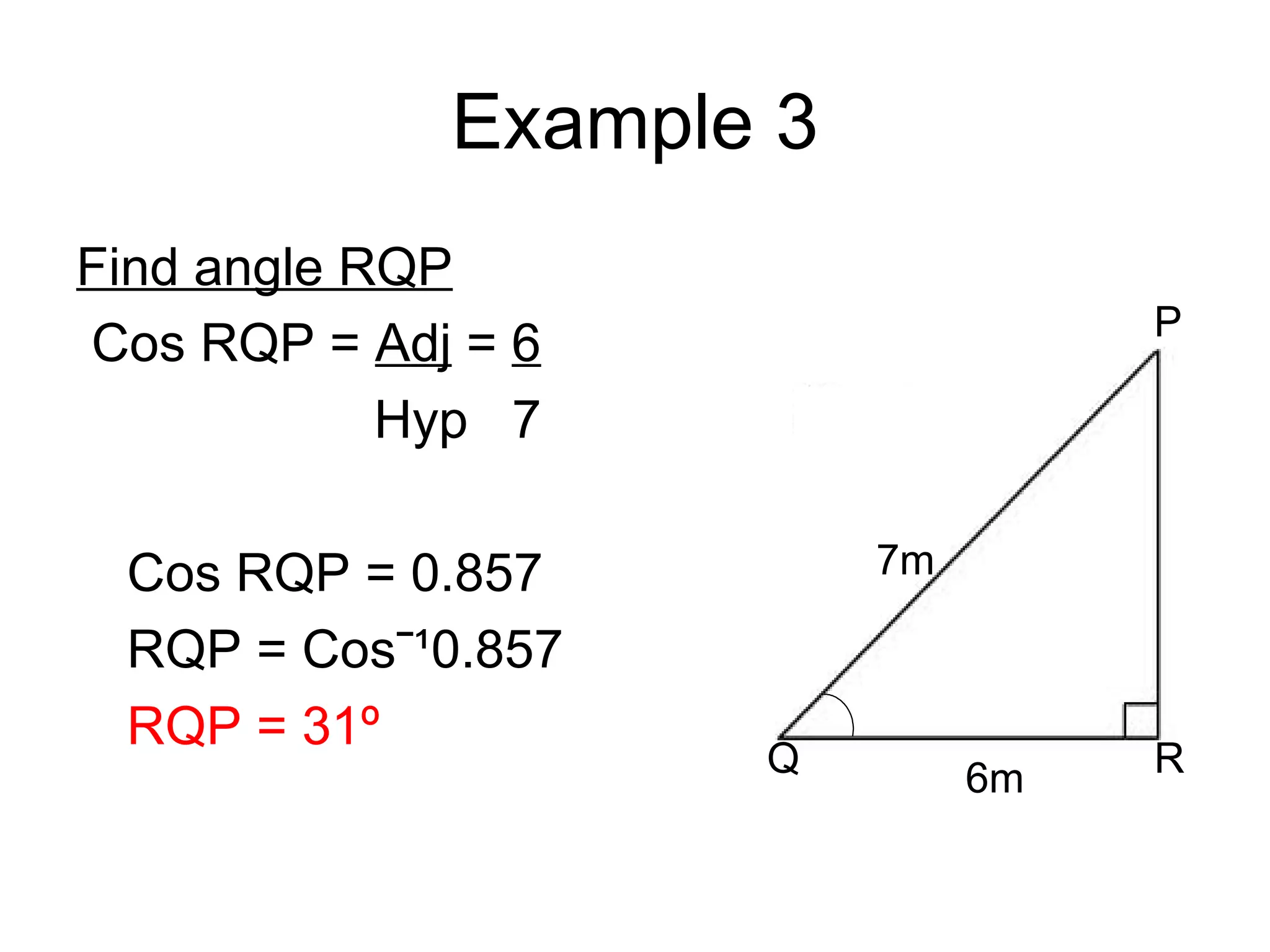
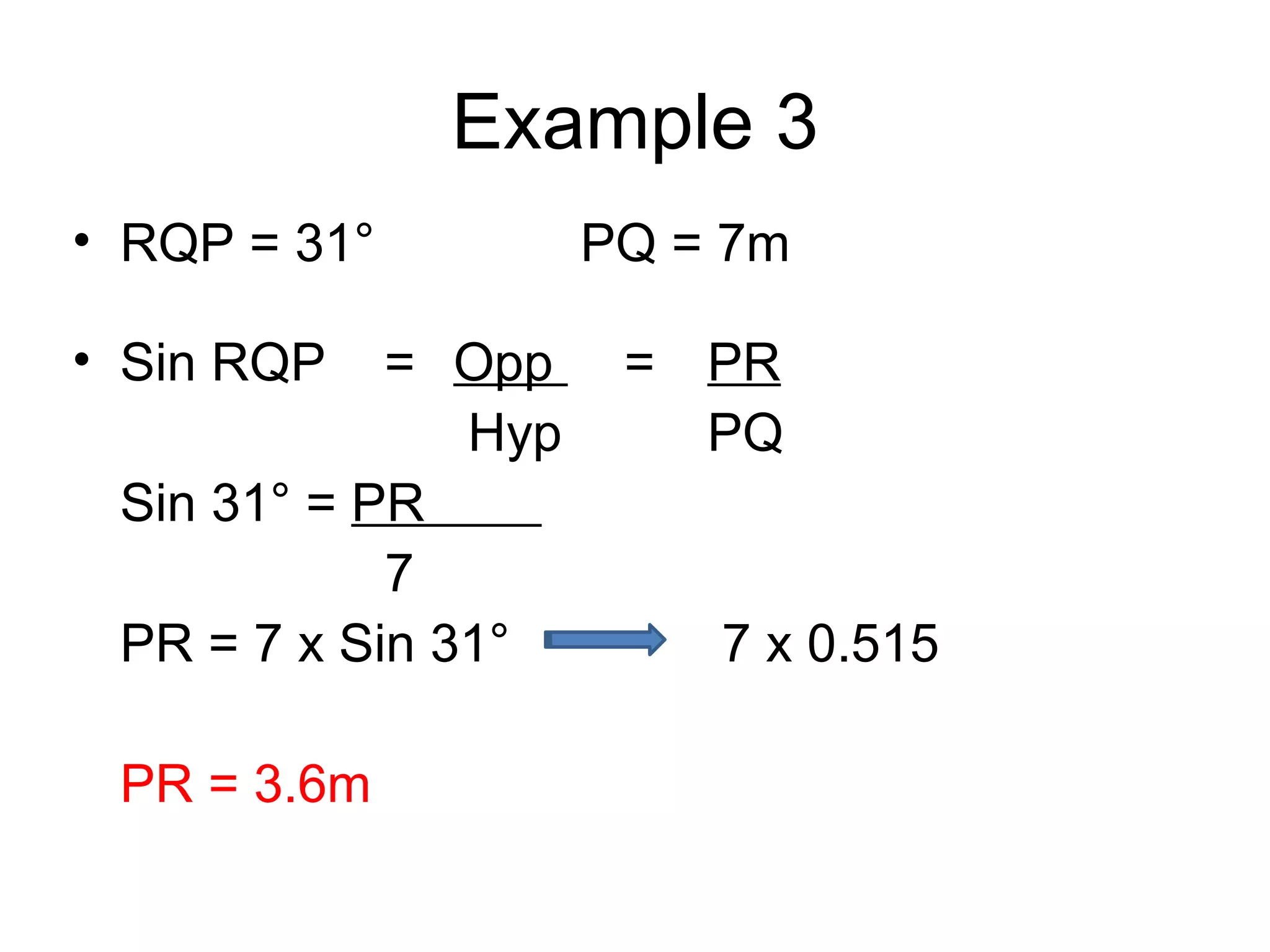
This document provides an introduction to trigonometry and examples of how to use trigonometric ratios to calculate angles and side lengths in right triangles. It defines the trigonometric ratios of sine, cosine, and tangent using the acronyms SOHCAHTOA. Examples are given to find missing angle measures and side lengths by setting up and solving equations involving trigonometric functions of the known ratios. The objectives are to calculate angles and side lengths and perform calculation checks in right triangles.

1. Trigonometry

2. Lesson Objectives Calculate the value of angles in a right angled triangle using trigonometric ratios. Apply trigonometry to perform calculation checks. Calculate the length of a side in a right angled triangle using trigonometric ratios.

3. Trigonometric Ratios SOHCAHTOA Sine Ɵ = opposite__ hypotenuse Cosine Ɵ = adjacent__ hypotenuse Tangent Ɵ = opposite adjacent

4. Example 2 Find the value of angles Ɵ and λ in triangle LMN. 13m 12m 5m θ λ

5. Example 2 Sin Ɵ = Opp = 12 = 0.923 Hyp 13 Ɵ = Sinˉ¹0.923 Ɵ = 67.38º Sin λ = Opp = 5 = 0.385 Hyp 13 λ = 22.62º

6. Trigonometry Check Check:180º - 90° - 67.38° = 22.62° Sin λ = 22.62° Cos λ = 12 = 0.923 Cos λ = 22.62° 13 Tan λ = 5 = 0.416 Tan λ = 22.62° 12

7. Example 3 Find the value of angles QPR and RQP and the length of the side PR. 7m 6m Q P R

8. Example 3 Find angle QPR Sin QPR = Opp = 6 Hyp 7 Sin QPR = 0.857 QPR = Sinˉ¹0.857 QPR = 59º 7m 6m Q R P

9. Example 3 Find angle RQP Cos RQP = Adj = 6 Hyp 7 Cos RQP = 0.857 RQP = Cosˉ¹0.857 RQP = 31º 7m 6m Q P R

10. Example 3 RQP = 31° PQ = 7m Sin RQP = Opp = PR Hyp PQ Sin 31° = PR 7 PR = 7 x Sin 31° 7 x 0.515 PR = 3.6m

11. Lesson Objectives Calculate the value of angles in a right angled triangle using trigonometric ratios. Apply trigonometry to perform calculation checks. Calculate the length of a side in a right angled triangle using trigonometric ratios.