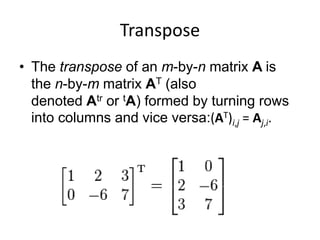
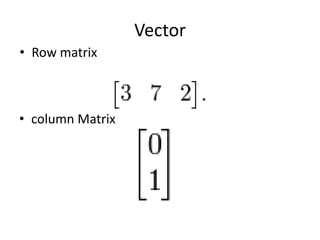
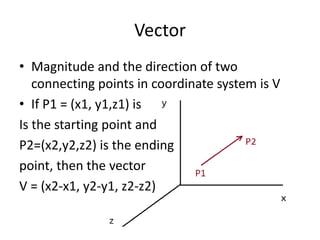
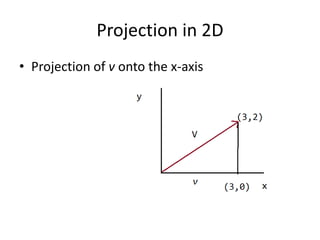
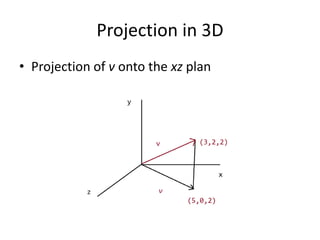
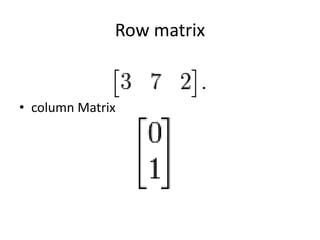
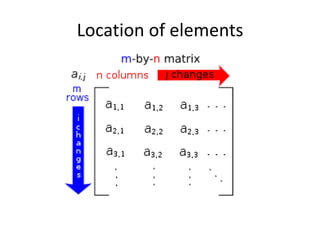
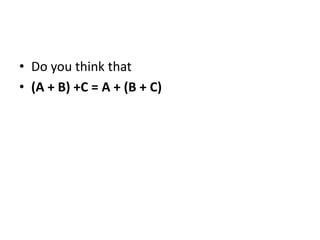A matrix is an arrangement of numbers organized into rows and columns. It has a specific number of rows and columns called its dimensions. Each individual number in the matrix is called an element, which has a specific location defined by its row and column. A square matrix has the same number of rows and columns. Matrices are useful in computer graphics for transformations and are typically denoted with a capital letter indicating their dimensions. To be equal, two matrices must have the same dimensions and corresponding elements must be identical.

1. Mathematics Fundamentals

2. Matrix

3. Matrix
• A matrix is a collection of numbers arranged
into fixed number of rows and columns
• C
R

4. • Each number that makes up a matrix is called
an element of the matrix.
• The element in a matrix have specific location

5. • The numbers of rows and columns of a matrix
are called its dimensions
• Here it is 4x3

6. • 2x3

7. Squire matrix
• A matrix with the number of rows==columns
• In CG squire matrices are used for
transformation

8. Row matrix
• column Matrix

9. Notation
• Usually a capital letter in bold face like
• A or M
• Sometimes as a reminder the dimensions are
written to the right of
• the letter as in B3x3

10. Location of elements

11. • If 2 matrices contain the same No. as
elements; are the 2 matrices equal to each
other???

12. • If 2 matrices contain the same No. as
elements; are the 2 matrices equal to each
other???
• No, to be equal, must have the same
dimensions and must have the same values in
the same positions.

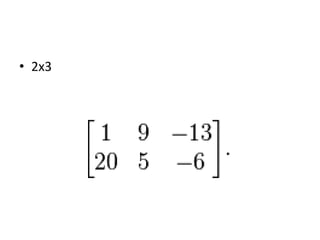
13. • In other words, say that An x m = [ai j] and that
Bp x q = [bi j]
• Then A = B if and only if n=p, m=q, and ai j =bi j
for all I and j in range

14. Zero matrix
• Which has all its elements zero
•

15. Adding
• The sum A+B of two m-by-n
matrices A and B is calculated entry wise:
• (A + B)i,j = Ai,j + Bi,j, where 1 ≤ i≤ m and 1
≤ j ≤ n.

16. • Do you think that
• (A + B) +C = A + (B + C)

17. • Do you think that
• (A + B) +C = A + (B + C)
• Yes

18. Scalar multiplication
• The scalar multiplication cA of a
matrix A and a number c (also called
a scalar in the parlance of abstract
algebra) is given by multiplying every entry
of A by c:(cA)i,j = c · Ai,j.

19. Transpose
• The transpose of an m-by-n matrix A is
the n-by-m matrix AT (also
denoted Atr or tA) formed by turning rows
into columns and vice versa:(AT)i,j = Aj,i.

20. • Familiar properties of numbers extend to these
operations of matrices
• for example, addition is commutative, i.e., the
matrix sum does not depend on the order of the
summands: A + B = B + A.
• The transpose is compatible with addition and
scalar multiplication, as expressed by (cA)T = c(AT)
and
• (A + B)T = AT + BT.
• Finally, (AT)T = A.

21. • The identity matrix In of size n is the n-by-n
matrix in which all the elements on
the main diagonal are equal to 1 and all
other elements are equal to 0, e.g.

22. • It is called identity matrix because
multiplication with it leaves a matrix
unchanged: MIn = ImM = M for any m-by-n
matrix M.

23. Vector
• Row matrix
• column Matrix

24. Vector
• Magnitude and the direction of two
connecting points in coordinate system is V
• If P1 = (x1, y1,z1) is
Is the starting point and
P2=(x2,y2,z2) is the ending
point, then the vector
V = (x2-x1, y2-y1, z2-z2)

25. Projection in 2D
• Projection of v onto the x-axis

26. Projection in 3D
• Projection of v onto the xz plan

27. • The magnitude (length) of a vector :
Derived from the Pythagorean theorem
– The direction of the vector:
α is angular displacment from the
x-axis
α

28. 3D
• The magnitude is simple extension of 2D
• Direction:
• Needs 2 angles to fully describe directions
• Latitude/longitude is a real word example

29. • α, β, y are the positive angles that the vector
makes with each of the positive cordinate axes
x,y and z respectivly

30. Normalizing
• Shrinking or stretching it so its magnitude is 1
– Creating unit vector
– Does not change the direction
• Normalize by dividing on its magnitude:

31. • It doesn’t come out to exactly 1, this is bcz of
the error using only 2 decimal places