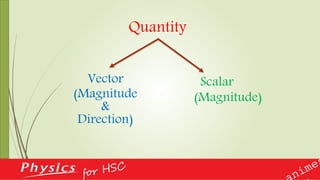
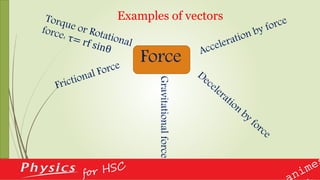
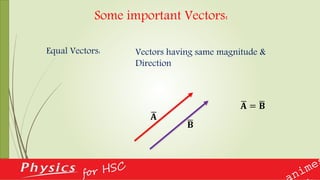
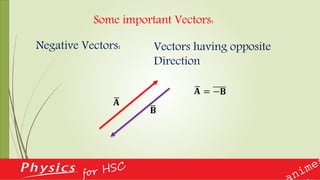
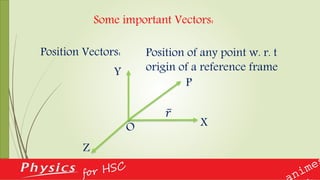
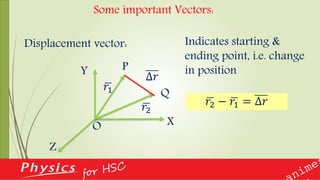
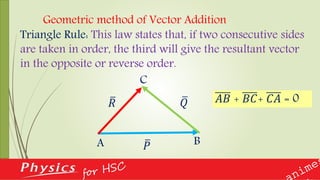
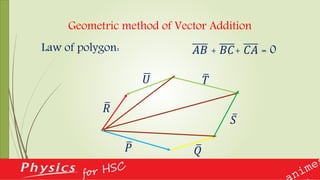
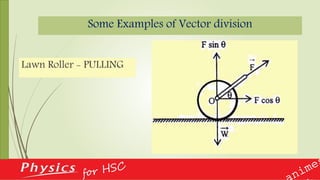
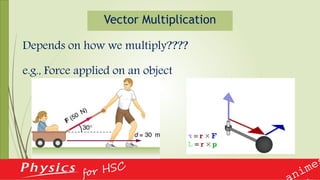
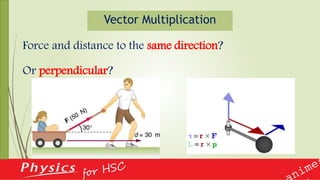
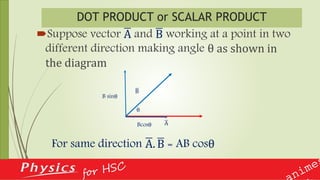
This document provides an overview of vectors and their applications in physics. It defines vectors and differentiates them from scalars, discusses vector notation and representation, and covers key concepts like addition, subtraction, and multiplication of vectors. Examples are given of vector quantities like displacement, velocity and force. The document also explains vector operators like gradient, divergence and curl, which allow converting between scalar and vector quantities, and outlines how calculus is important in physics for studying change.









































![Vector Multiplication
h) Find the normal projection of A on B. [Hints: A.B = ABcosθ]
If A = i +3j + 2k and B = i + 2j - k and C = 2i - 3j +4k then
e) Find the magnitude of the unit vector A.
f) Prove that (B + C) X A = B X A + CX A
g) Prove that the vectors A and B are coplanar](https://image.slidesharecdn.com/ch2vector-170623100308/85/Ch-2-vector-65-320.jpg)
![b) Perpendicular to each other? [Hints: use dot product]
If A = 5i +2j - 3k and B = 15i - mj -9k then for what value
of m the vectors will be
a) parallel to each other? [Hints: use cross product]](https://image.slidesharecdn.com/ch2vector-170623100308/85/Ch-2-vector-66-320.jpg)
![Scalar product of two vectors is 18 unit and
magnitude vector product is 6√3. Find the angle
between the vectors. [300]](https://image.slidesharecdn.com/ch2vector-170623100308/85/Ch-2-vector-67-320.jpg)







![Mathematical Problems
Determine angle between two vectors of magnitude A = 3i +3j - 3k and B = 2i +j+
k. [Hints:A.B = ABcosθ]
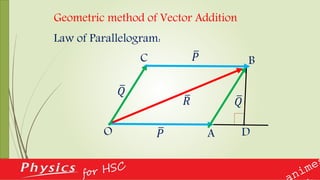
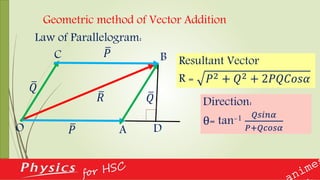
If two vectors acting simultaneously at a point are equal, show that their resultant
bisects the angle between those vectors.
A boat starts rowing with velocity 20 ms-1 along the width of a river. The velocity of
the current of the river is 15 ms-1. Determine the resultant velocity of the boat. If
the river is of width 3 km, what will be the time required by the boat to reach the
other side of the river? [Hints: R= P2 + Q2 + 2PQcosα and t=d/v] ans: 25
ms-1 and 150s](https://image.slidesharecdn.com/ch2vector-170623100308/85/Ch-2-vector-75-320.jpg)
![Mathematical Problems
A boat velocity is 18 kmh-1 towards the river current and 6 kmh-1 against the
current. At what direction the boat needs to move so that it will reach to the shore
perpendicularly. What will be the velocity of boat then?
A man while running at velocity 3 ms-1 comes across rain falling vertically of
velocity 6 ms-1. At what angle he will have to hold an umbrella to protect himself
from rain? [Hints: tanθ] 26034’](https://image.slidesharecdn.com/ch2vector-170623100308/85/Ch-2-vector-76-320.jpg)
![Mathematical Problems
If A = i +3j + 2k and B = i + 2j - k and C = 2i - 3j +4k then
a) Determine scalar and vector product of the vectors A and B.
b) Find a unit vector perpendicular to the plane of two vectors A and B.
c) Determine the magnitude of A.
d) Find a unit vector A.
e) Find the magnitude of the unit vector A.
f) Prove that (B + C) X A = B X A + CX A
g) Prove that the vectors A and B are coplanar
h) Find the normal projection of A on B. [Hints: A.B = ABcosθ]](https://image.slidesharecdn.com/ch2vector-170623100308/85/Ch-2-vector-77-320.jpg)
![Mathematical Problems
If A = 5i +2j - 3k and B = 15i - mj -9k then for what value of m the vectors will
be
a) parallel to each other? [Hints: use cross product]
b) Perpendicular to each other? [Hints: use dot product]
A force F = (6i - 3j +2k)N acts upon a particle and produces a displacement r = (2i
+ 2j - k) m. calculate the work done by the force.
If A + B = A − B then show that A is perpendicular toB.
Prove that A. B 2 + AXB 2 = A2B2
The position vector of a particle is r = 2ti + 2t2j where t is time. determine it’s a)
velocity, b) acceleration](https://image.slidesharecdn.com/ch2vector-170623100308/85/Ch-2-vector-78-320.jpg)
![Mathematical Problems
If A = 5i +2j - 3k and B = 15i - mj -9k then for what value of m the vectors will
be
A = i 2x + y + j 3y + z2 + k(az + x) will be solenoidal?
[Hints: 𝛻. A = 0]
A = i 2x + y + j 3y + z2
+ k(az + x) will be rotational or irrotational?
A = 2i - 2j + k and B = i + j +2k
a) Determine projection of A on B
b) Are θ1 and θ2 equal? Show.](https://image.slidesharecdn.com/ch2vector-170623100308/85/Ch-2-vector-79-320.jpg)
![Mathematical Problems
Two vectors, A = xi +yj + zk and B = pi +qj + rk are parallel to each other then
show that
x
y
=
p
q
,
y
z
=
q
r
and
z
x
=
r
p
If φ= 2xy4 – x2z then, find 𝛻φ at (2, -1, -2)
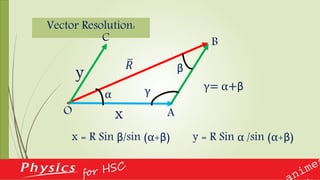
Two vector quantities F1 andF2 are working at the same point whereas F1 = 10 unit
and it acts at 300 with the ground and F2 = 5 unit acts perpendicularly. Determine
horizontal and perpendicular component of the resultant. [8.66 unit and 10 unit]
Hints: horizontal component R cosθ = F1cosα1 + F2 cosα2 And vertical component R
cosθ = F1sinα1 + F2 sinα2](https://image.slidesharecdn.com/ch2vector-170623100308/85/Ch-2-vector-80-320.jpg)
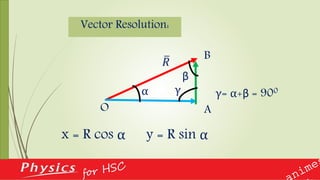
![Mathematical Problems
Determine angular distance between A = i - 2j + 2k and x, y and z axis.
[Hints: Find α, β and γ
A .i = Ai cos α and α = ?
A .j = Aj cos β and β = ?
A . k = Ak cos γ and γ = ?]](https://image.slidesharecdn.com/ch2vector-170623100308/85/Ch-2-vector-81-320.jpg)
