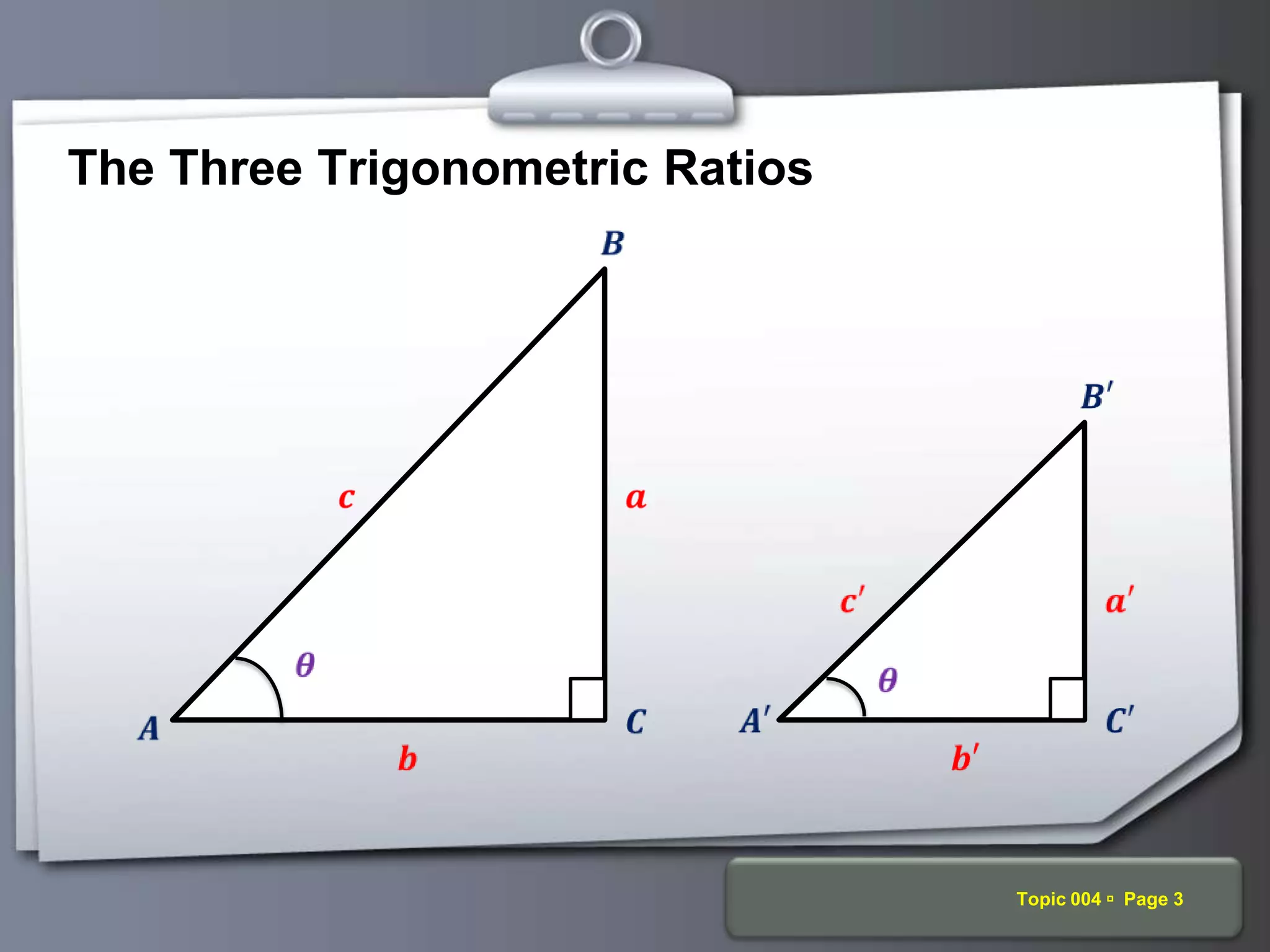
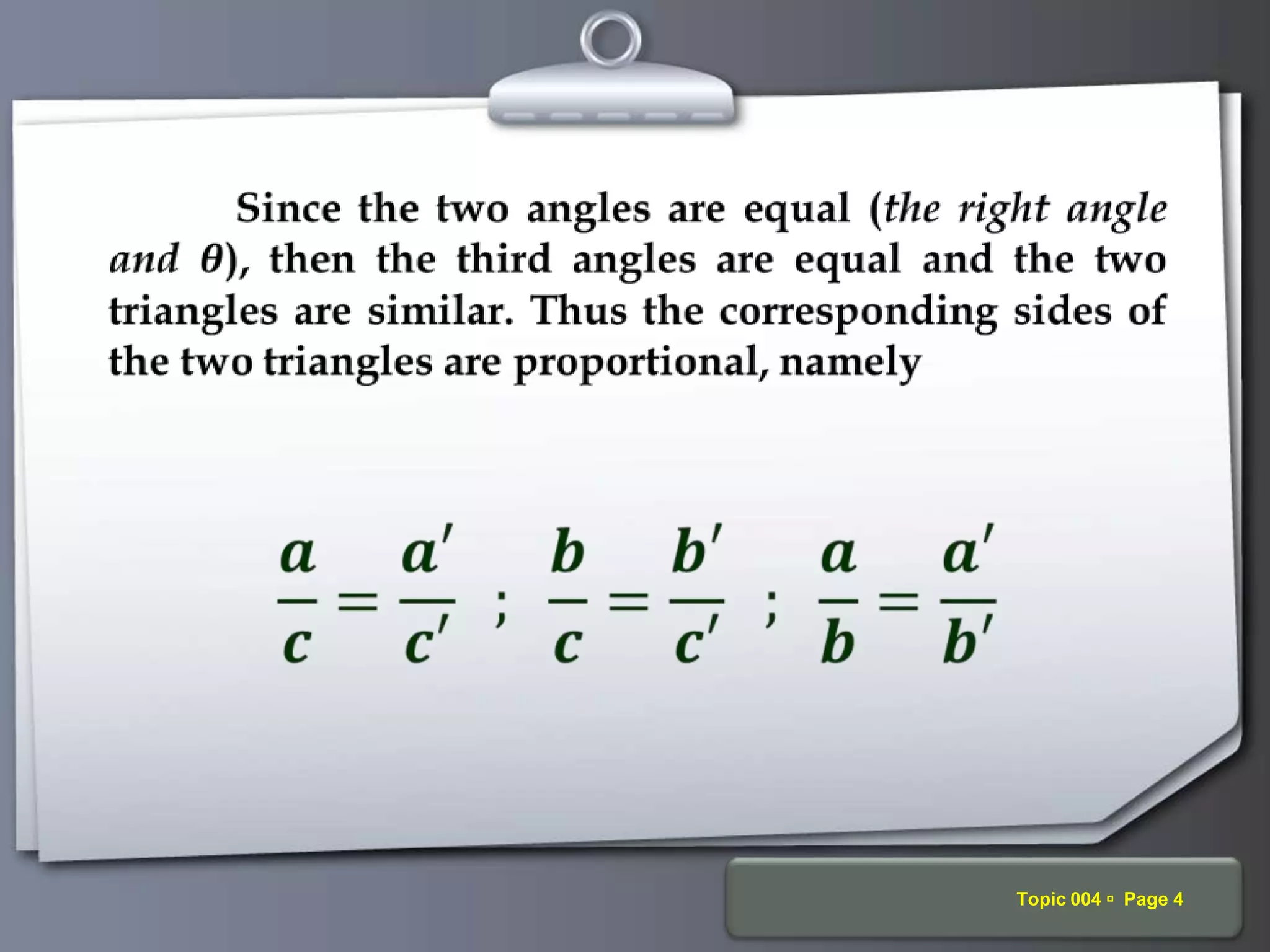
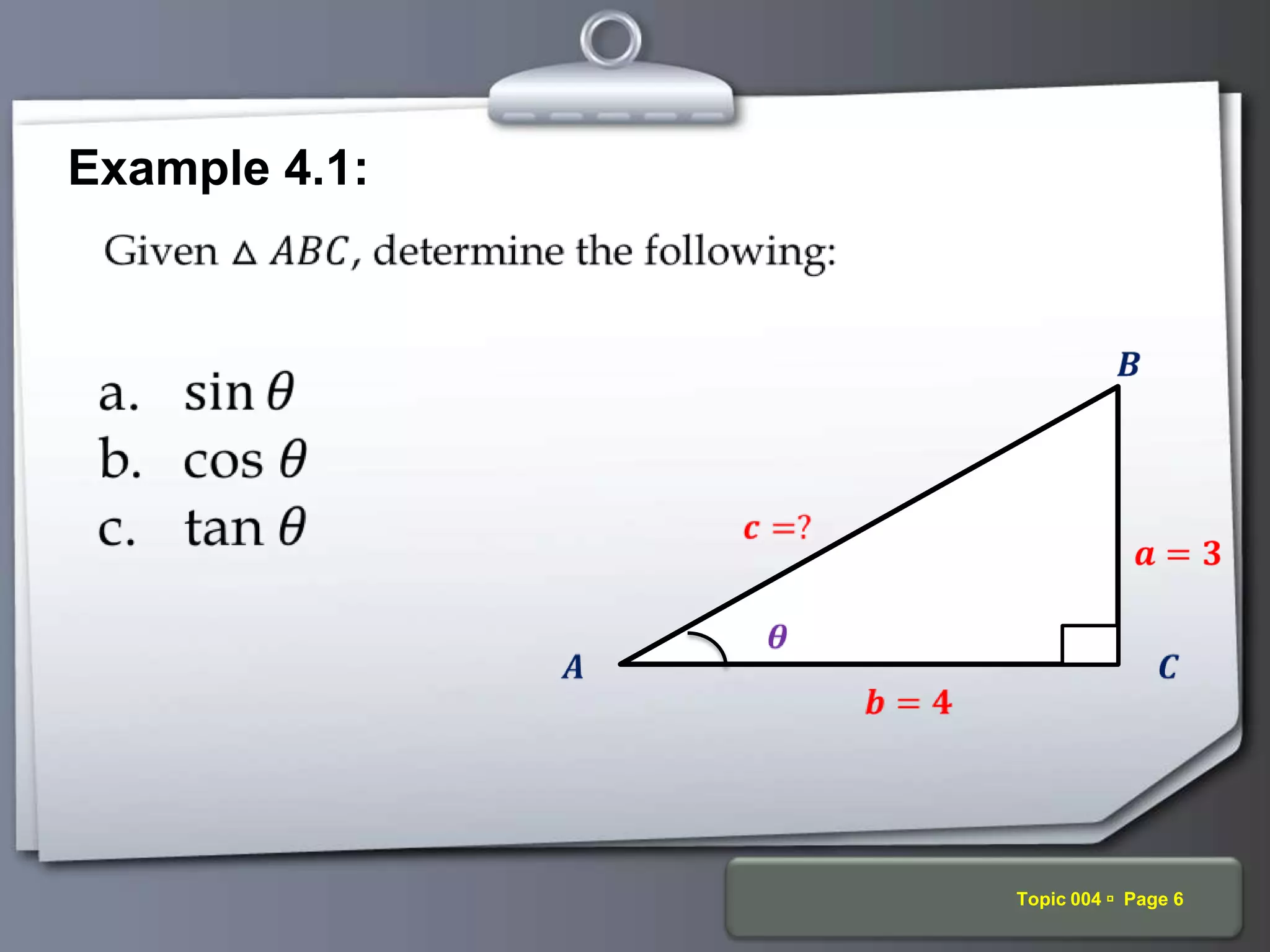
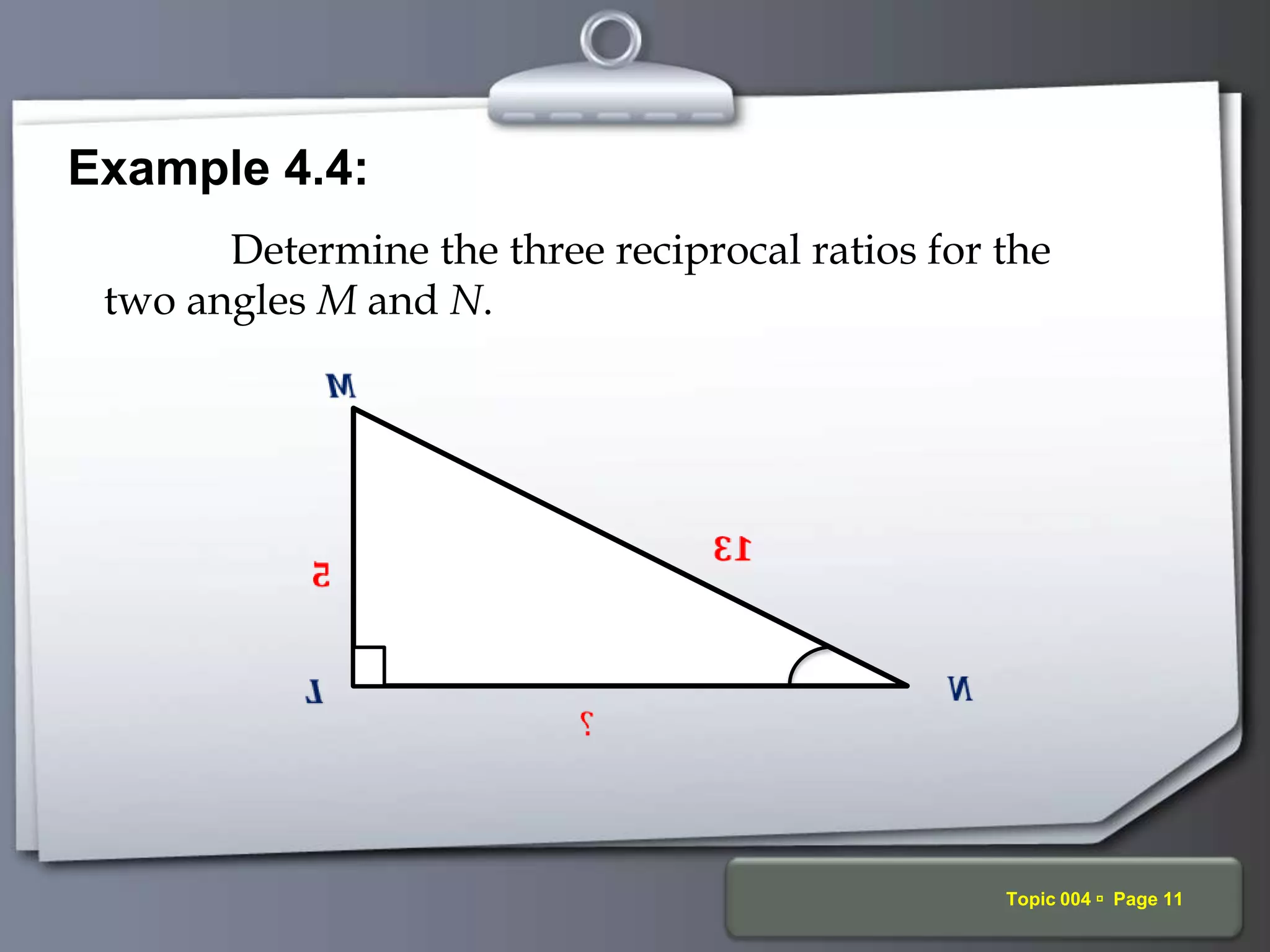
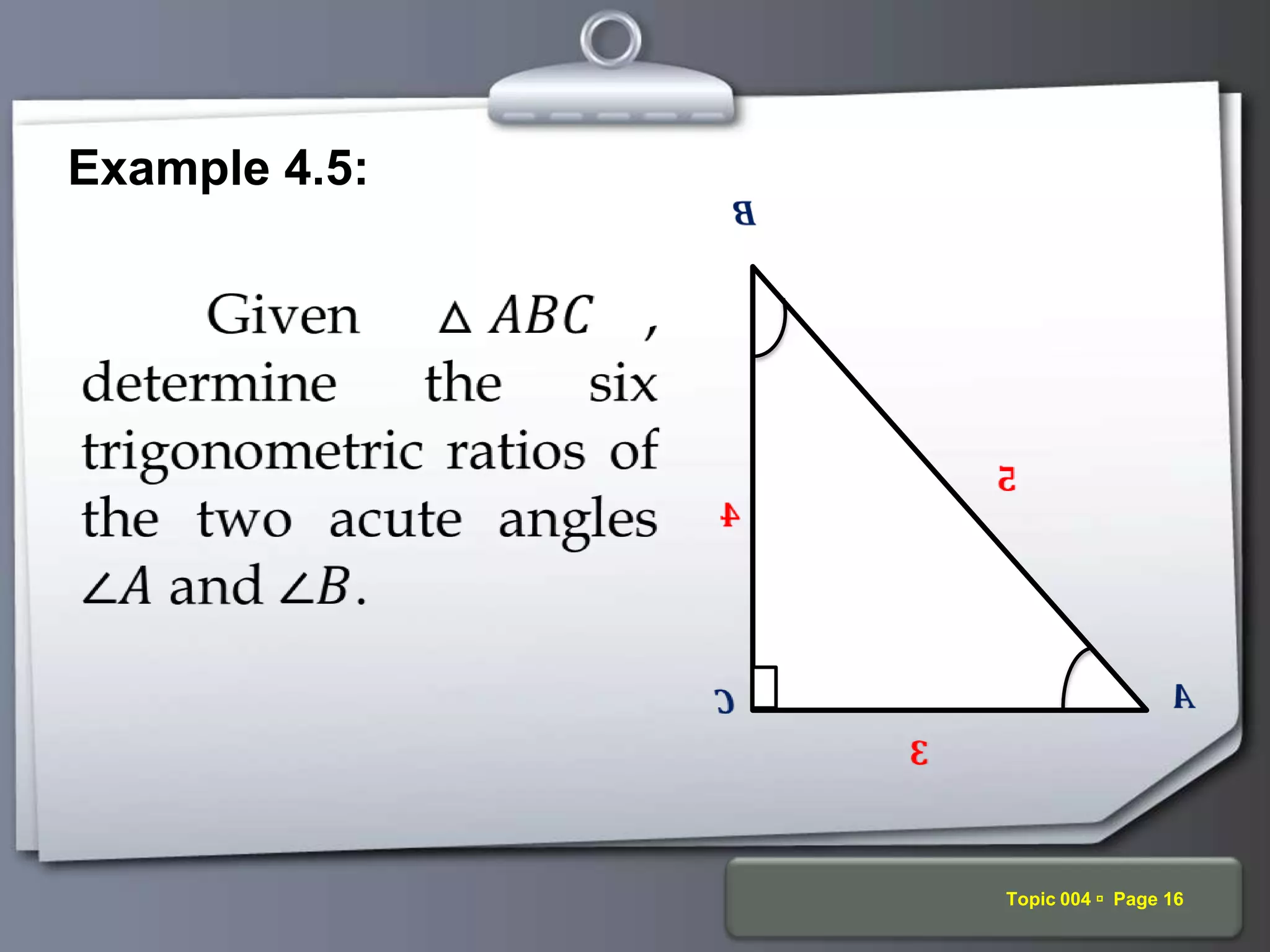
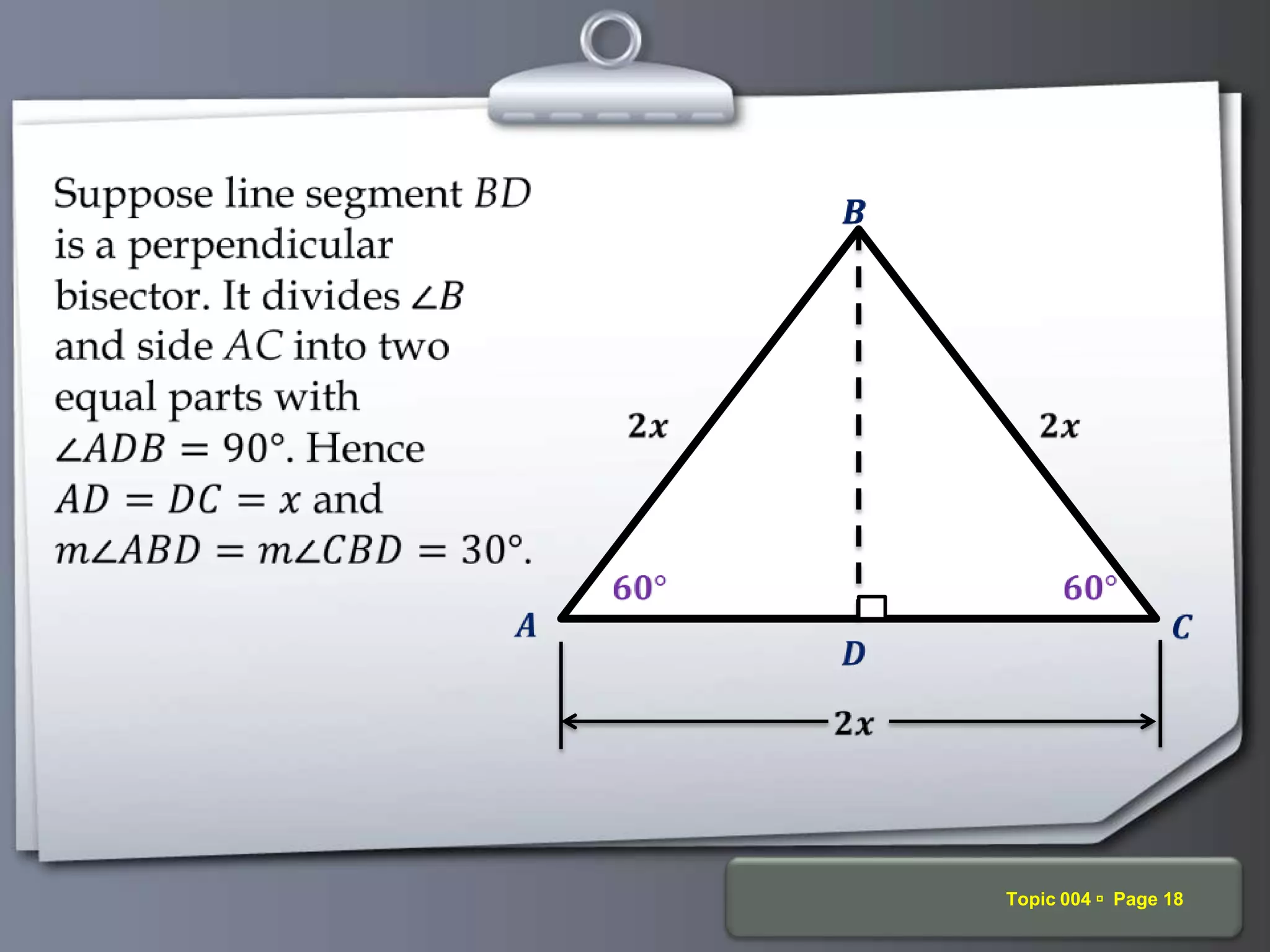
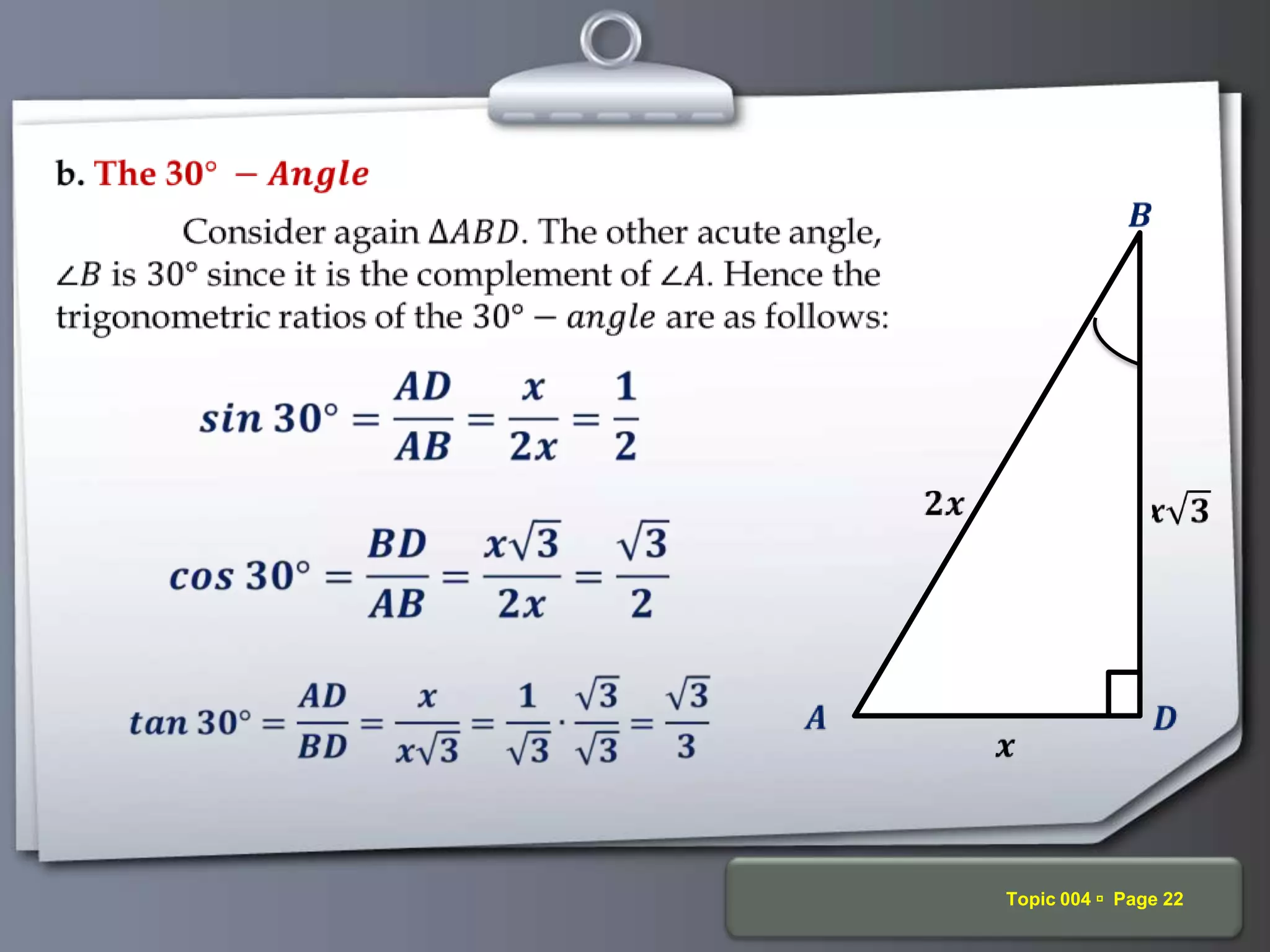
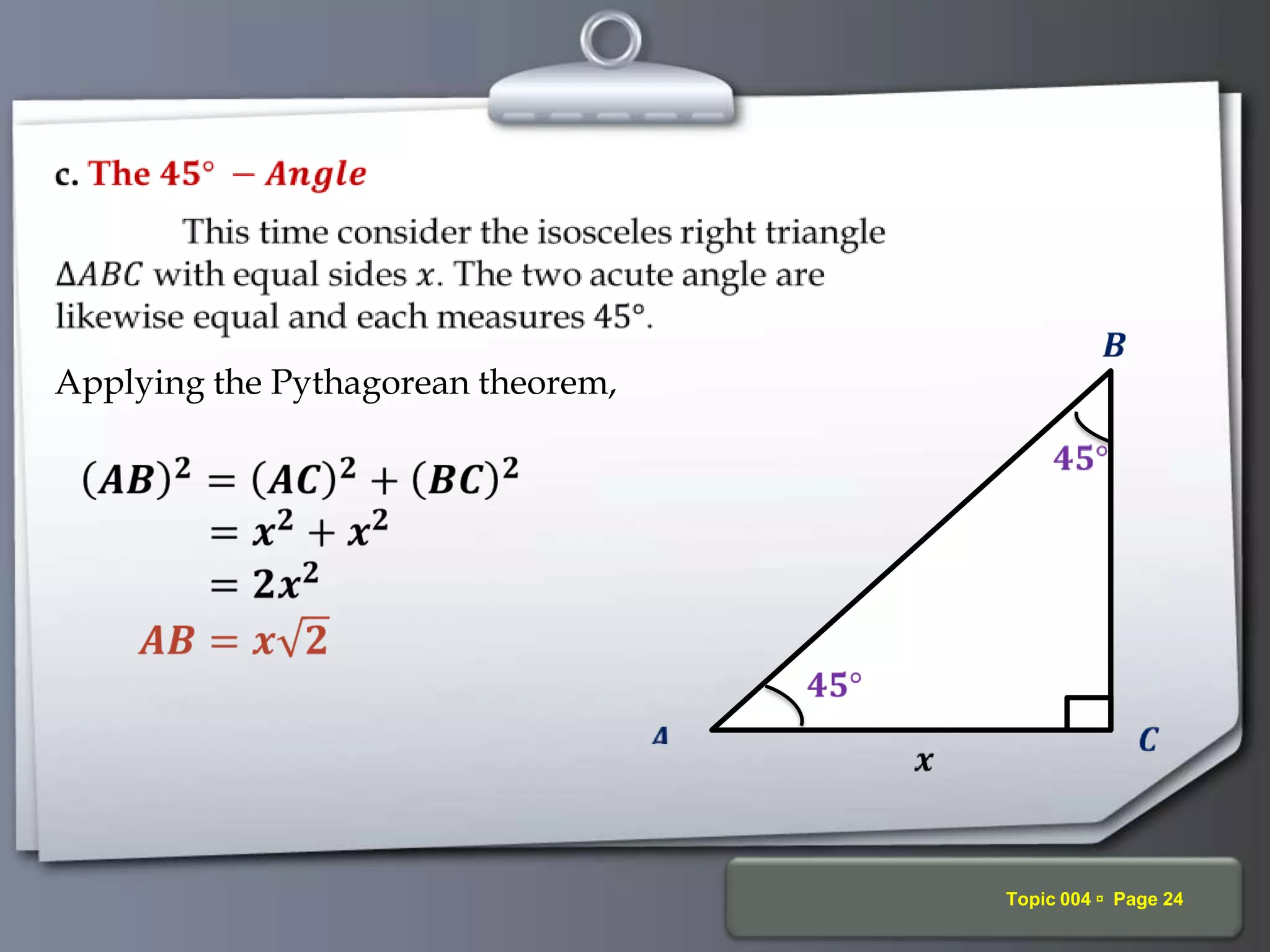
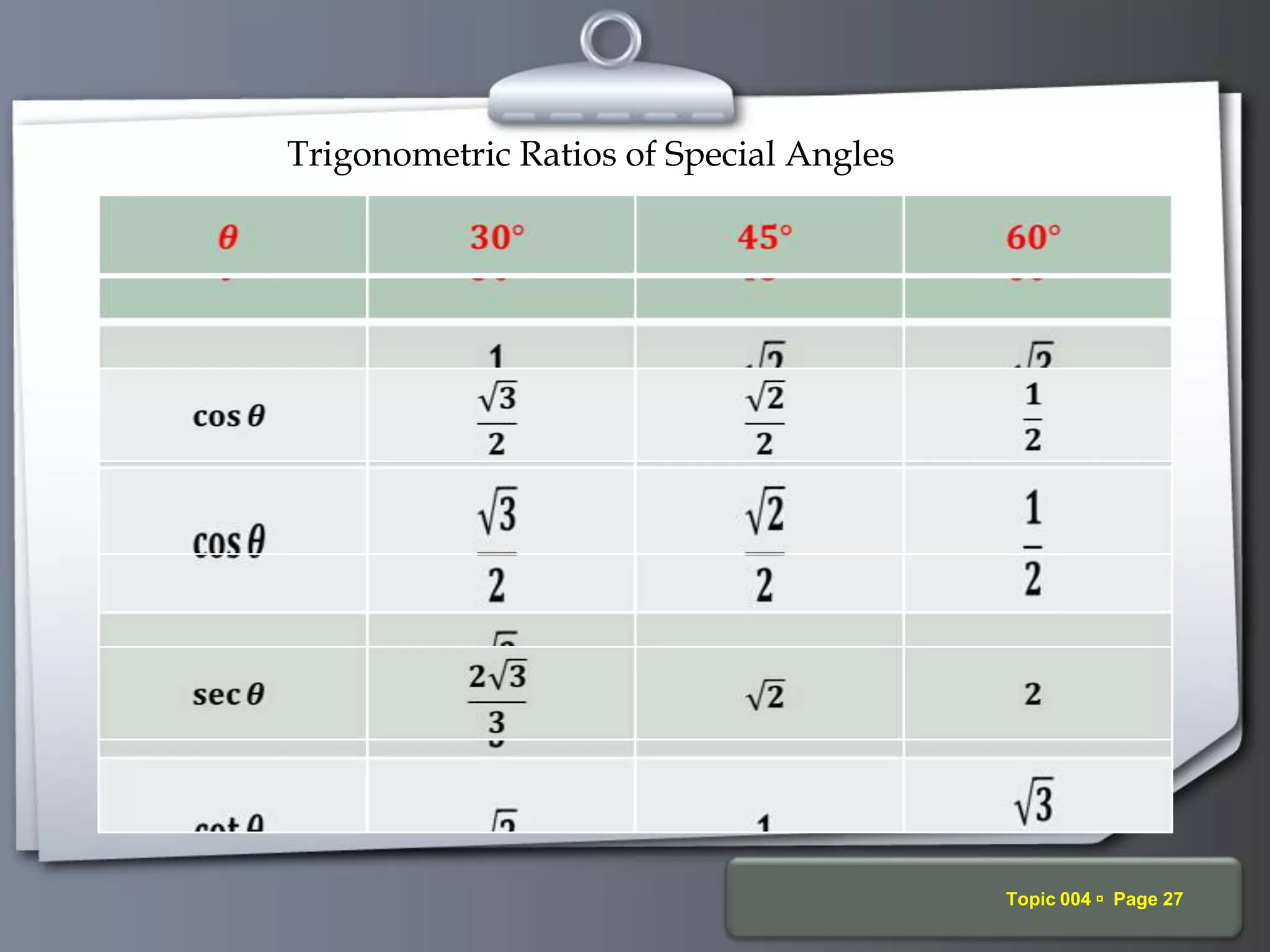
The document discusses trigonometric ratios and their properties. It defines the three basic trigonometric ratios - sine, cosine, and tangent - for any angle. It also discusses reciprocal ratios like cosecant, secant, and cotangent, which are the reciprocals of the basic ratios. The document provides examples of calculating trigonometric ratios for various angles and triangles. It also examines ratios of complementary and special angles like 0, 30, 45, 60, 90 degrees.