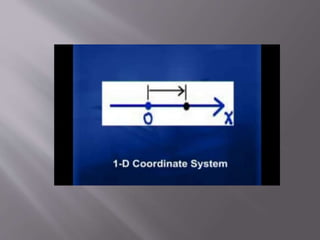
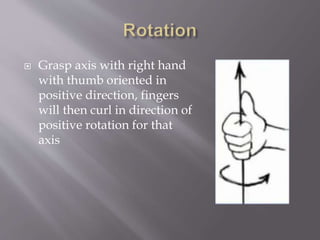
Human eyes perceive 3D projections in 2D. Coordinate systems including 1D, 2D, and 3D Cartesian systems define locations using reference points and orthogonal axes. 3D systems use x, y, and z coordinates to locate points and define geometries in space, including volumes like cubes and spheres. Coordinate transformations allow changing between reference frames.

2.  Human eyes see object defiantly


3.  3D projection is in 2 D

4.  Are the measured frame of reference within
which geometry is defined, manipulated and
viewed
 In this system, a point serves as the origin, and
three lines (axes) that pass through this point
and are orthogonal to each other (at right
angles 90 degrees)

5.  1D coordinate system
 2D coordinate system
 3D coordinate system

6.  Direction and magnitude along a single axis,
with reference to origin
 Location are defined by a single coordinate

7.  We can define points, segments, lines rays
 Can have multiple origins (frame of reference)
and transform coordinates among them

9.  Direction and magnitude along two axes, with
reference to an origin
 Location are defined by x, y coordinate

10.  We can define points, segments, lines rays,
curves, polygons (any other planar geometry)
 Can have multiple origins (frame of reference)
and transform coordinates among them

12.  3D Cartesian coordinate system
 Direction and magnitude along three axes, with
reference to an origin
 Location are defined by x, y, z coordinate

13.  We can define points, segments, lines rays,
curves, polygons (any other planar geometry)
and cubes, cones, spheres, etc. (volume in
space)
 Can have multiple origins (frame of reference)
and transform coordinates among them

15.  right hand rules etc.
 These rules determine orientation of axes and
direction of rotations
 Thumb = pos x
 Index up = pos y
 Middle out = pos z

16.  Most world and objects axes tend to be right
handed
 Left hand axes often are used for cmaeras

18.  Grasp axis with right hand
with thumb oriented in
positive direction, fingers
will then curl in direction of
positive rotation for that
axis

19.  Right handed Cartesian coordinate system
describes the relationship of the x, y, z in the
following manner
 X is positive to the right of the origin and
negative to the left
 Y is positive to the above of the origin and
negative to the below
 Z is positive behind the origin and negative
beyond

20.  Z up typically used by designers
 Y up typically used by animators

21.  Application data will be transformed among
the various coordinate systems depending on
whats to be accomplished
 Individual coordinate systems often are
hierarchically linked within the scene

22.  Use OPP to make the object of the 3d points
 Class 3d-class
 { public:
 Float x;
 Float y;
 Float z;
 }

23.  Modeling is the process of describing an object
or scene so that we can construct an image of it
 Angle, location, size etc..
 Polygon strips or meshes
 Meshes provide a more economical description than
multiple individual polygons (wireframe model
 100 individual triangles, each have 3 vertices, would
require 100 x3 vertex definitions
 Triangle strips require n + 2 vertex definitions, n is
number of triangles in strip. For 100 needs 102
unique vertex definitions

24.  Meshes also provide continuity across surfaces
which is important for shading calculations

26.  With cured surfaces the accuracy of the
approximation is directly proportional to the
number of polygons used in the representation
 More polygons yield a better approximation
 But more polygons also exact greater
computational overhead..

27.  The process of computing a 2d image using a
combination of a 3 D database, scene
characteristics and viewing transformations
 Various Alog. According to the need of
applications

28.  The subdivision of an entity or surface into one
or more non-overlapping primitives
 Typically, renderers decompose surfaces into
triangles as part of the rendering

31.  The process of selecting a representative but
finite number of values along a continuous
function sufficient to render a reasonable
approximations of the function for the task at
hand

32.  To improve rendering efficiency when
dynamically viewing a scene, more or less
detailed versions of a model may be swapped
in and out of the scene database depending on
the importance of the object in current view

33.  A vector perpendicular to a surface and
outward facing
 SN are used to determine visibility and also in
the calculation of shading values