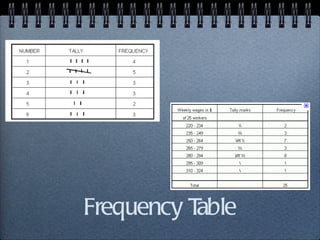
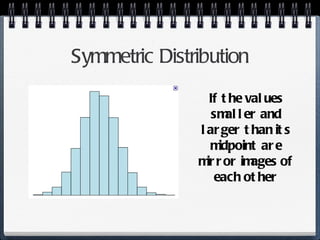
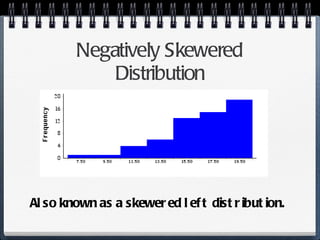
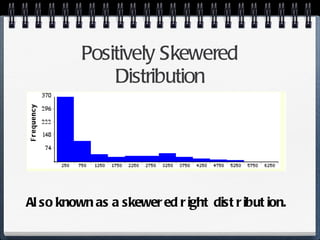
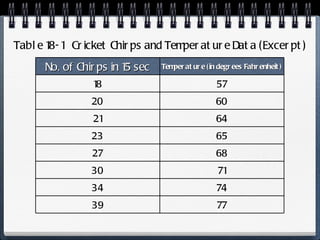
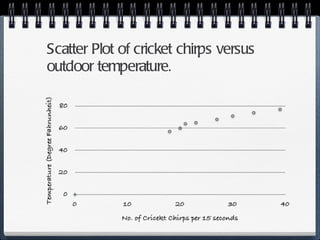
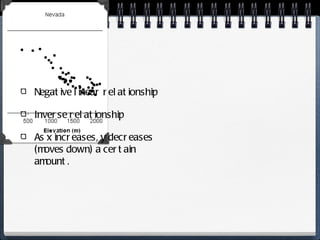
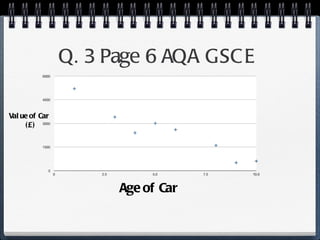
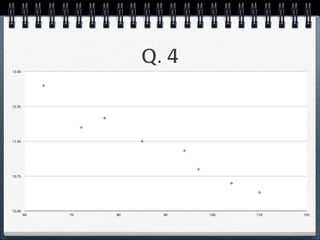
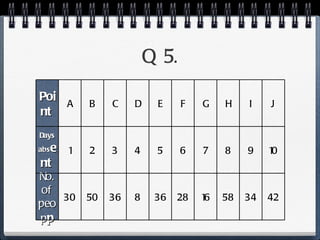
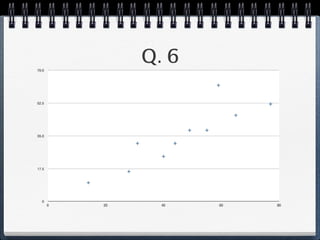
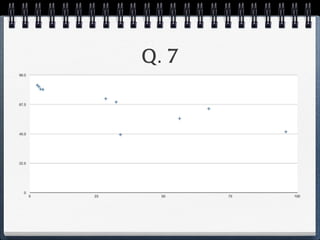
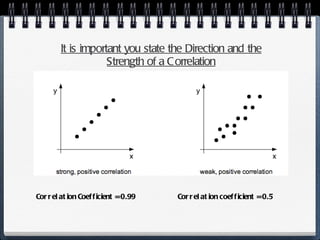
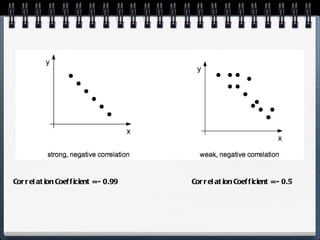
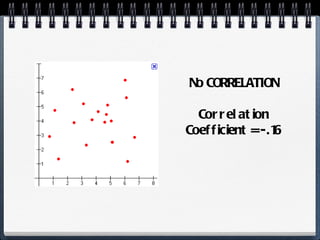
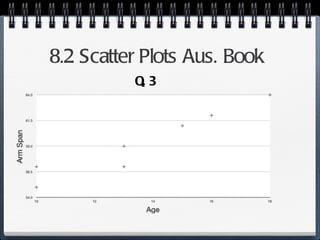
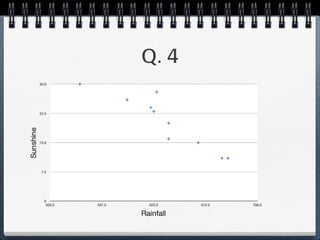
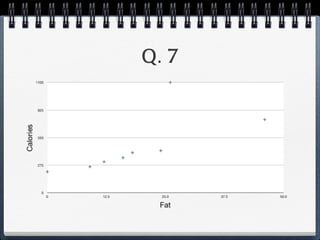
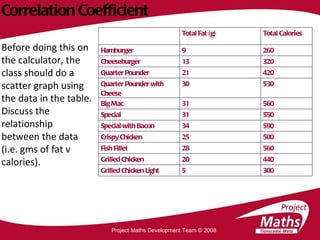
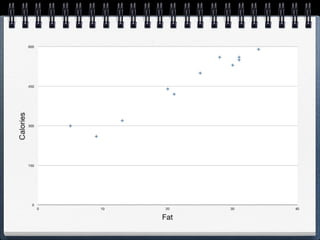
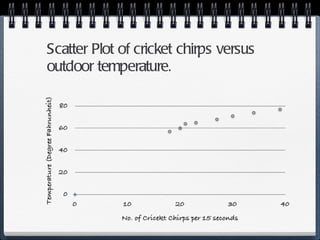
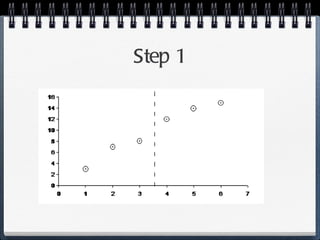
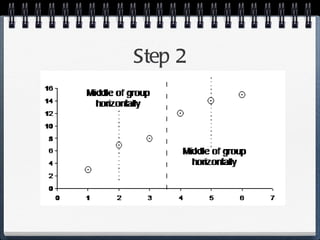
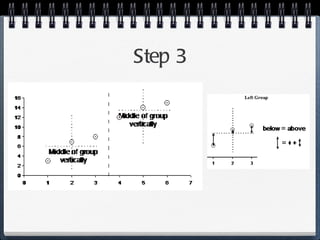
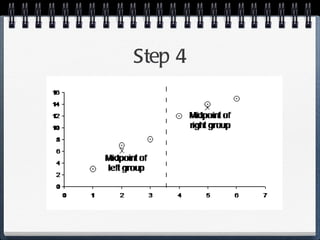
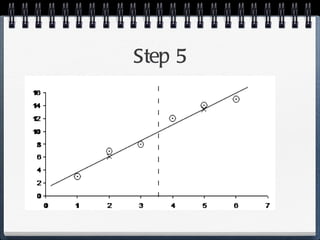
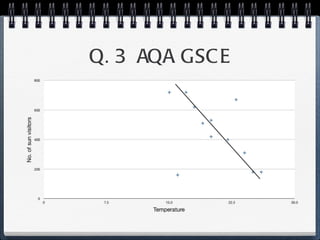
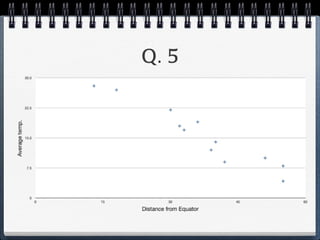
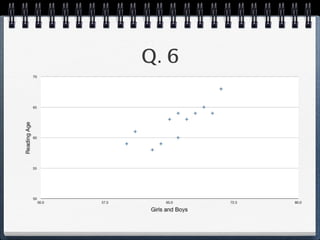
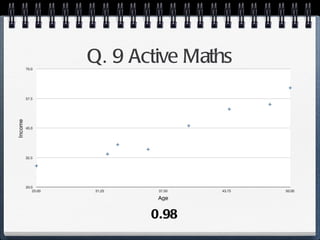
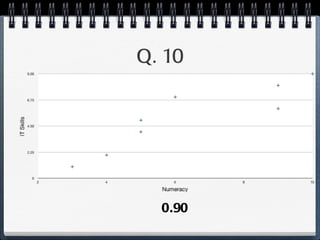
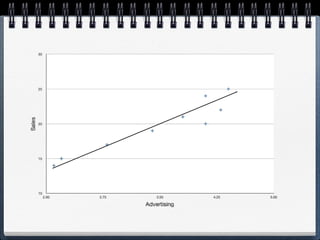
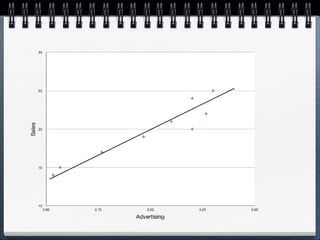
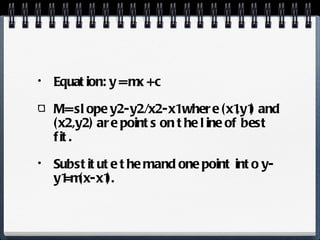The document discusses different statistical methods for organizing and summarizing data, including frequency tables, stem-and-leaf plots, histograms, and scatter plots. It provides examples of each method and explains how to interpret the results, such as looking for relationships between variables in scatter plots. Key terms defined include correlation, variables, and linear regression lines.

1. Frequency Tables Ms. Carter Leaving Certificate

2. Tally Marks Tally marks are a way to count things in groups of five. You draw four vertical lines and on the fifth you draw a diagonal line across the previous four.

3. Example: Counting Apples

4. Tally Marks

5. You tally now!

6. Frequency Table

7. What type of jobs use frequency tables?

8. EXAMPLE

9. The marks awarded for an assignment set for a Year 8 class of 20 students were as follows: 6 7 5 7 7 8 7 6 9 7 4 10 6 8 8 9 5 6 4 8 Present this information in a frequency table. Step 1 Step 2 Step 3 Now you try! Page 17 Question 1!

10. Solutions to Exercise 1.3 Result 3 Heads 2 Heads 1 Head 0 Heads Tally Frequency 3 11 9 2

12. Stem-and-Leaf Diagrams and Stemplots A S & L diagram represents data by seperating each value into two parts: the stem (usually the leftmost digit) and the leaf. S & L diagrams represent data in a similiar way to bar charts. In stem-and-leaf plots, numeric data is shown by using the actual numerals. Stem-and-leaf plots are especially useful when you have a lot of data that has a wide range.

13. To make a Stemplot, follow these steps: The following stem-and-leaf plot shows the record of wins for the Eastern Conference NBA teams:

14. Back-to-Back S & L This S & L Diagram compares two data sets.

15. Histograms H. break the range of values of a variable into classes and display only the count or per cent of the observations that fall into each class. H. are used to represent CONTINUOUS NUMERICAL DATA!

16. The following frequency table shows the times, in minutes, spent by a group of woman in a boutique. Draw a histogram of the distribution. Time 0-10 10-20 20-30 30-40 40-50 Numbe r 1 4 8 7 9

17. Distribution of Data

18. Symmetric Distribution If the values smaller and larger than its midpoint are mirror images of each other

19. Negatively Skewered Distribution Also known as a skewered left distribution.

20. Positively Skewered Distribution Also known as a skewered right distribution.

21. What are Variables? Variables are things that we measure, control, or manipulate in research. They differ in many respects, most notably in the role they are given in our research and in the type of measures that can be applied to them. Variables are things that we measure, control, or manipulate in research. They differ in many respects, most notably in the role they are given in our research and in the type of measures that can be applied to them.

22. Looking for Links Correlations and Associations

23. National Institutes of Health (NIH) Sedentary activities (like Tv watching) are associated with an increase in obesity and an increase in the risk of diabetes in women. Anger expression may be inversely related to the risk of heart attack and stroke. (Those who express anger may have a decreased risk). Light-t-moderate drinking reduces the risk of heart disease in men.

24. News Reporters love to tell stories about the latest links! Such as.. Does having her first baby later in life cause a woman to live longer? (New York Times) Do we believe this or much of anything anymore?

25. ‘ Count Cricket Chirps to Gauge Temperature’ ( Garden Gate ) ) What you have to do! 1. find a cricket 2. count the number of times it chirps in 15 seconds 3. add 40 You’ve just predicted the temp. in degrees Fahrenfeit!

27. Table 18-1 Cricket Chirps and Temperature Data (Excerpt) No. of Chirps in 15 sec Temperature (in degrees Fahrenheit) 18 57 20 60 21 64 23 65 27 68 30 71 34 74 39 77

28. To make a Stemplot, follow these steps: The following stem-and-leaf plot shows the record of wins for the Eastern Conference NBA teams:

29. Bivariate Data

30. Two variables Tied or paired together Two - dimensional data Bivariate Data Deals with causes or relationships The major purpose of bivariate analysis is to determine whether relationships exist. Each observation is composed of..

31. Lets see another example!

32. A Press Release by Ohio State University Medical Center The headline says that... “ aspirin can prevent polyps in colon cancer patients”

33. Raw Data for this Study ID NO. 22292 GROUP=ASPIRIN DEVELOPED POLYPS=NO (635 LINES) Table 18-2 Summary of Aspirin v’s Polyps Study Results * total sample size = 635 (approx were half randomly assigned to each person) Group % Developing Polyps* Aspirin 17 Non-aspirin 27

34. Scatter Plots Bivariate Numerical Data Two Dimensions Horizontal dimension (x-axis) Vertical dimension (y-axis)

35. Scatter Plot of cricket chirps versus outdoor temperature.

36. Interpreting a Scatterplot you do this by looking for trends in the data as you go from left to right.

37. Positive linear relationship Proportional relationship As x increases (moves right one unit), y increases (moves up) a certain amount.

38. Negative linear relationship Inverse relationship As x increases, y decreases (moves down) a certain amount.

39. If the data don’t seem to resemble any kind of line (even a vague one) this means that no linear relationship exists.

40. Positive Linear Relationship as the cricket chirps increase so does the temperature aswell.

41. Q. 3 Page 6 AQA GSCE Age of Car Value of Car (£)

42. Q. 4

43. Q 5. Point A B C D E F G H I J Days abs ent 1 2 3 4 5 6 7 8 9 10 No. of peop p 30 50 36 8 36 28 16 58 34 42

44. Q. 6

45. Q. 7

46. Quantifying the Relationship Quantify or measure the extent and nature of the relationship.

47. We have already seen how to measure the direction of a linear relationship BUT you will also have to decide on the STRENGTH of the relationsbip!! Introduce the...

48. Correlation Coefficient Measures the strength and direction of the linear relationship between x and y (or the vertical and horizontal dimension).

49. Calculating the C.C. It is represented by the letter r It has a value between - 1 and 1 You only have to be able to calculate it using your calculator-luckily for you!

50. If r is close to 1, then there is a strong positive correlation between two sets of data. If r is close to -1, we say there is a strong negative correlation between the two sets. If r is close to 0, then there is no correlation between the two sets. Most statisticians like to see correlations above = 0.6 or below - 0.6.

51. Types of Correlation

52. It is important you state the Direction and the Strength of a Correlation Correlation Coefficient = 0.99 Correlation coefficient = 0.5

53. A positive correlation means that high values of one variable are associated with high values of a second variable . The relationship between height and weight, between IQ scores and achievement test scores, and between self-concept and grades are examples of positive correlation.

54. Correlation Coefficient = - 0.99 Correlation Coefficient = - 0.5

55. A negative correlation or relationship means that high values of one variable are associated with low values of a second variable. Examples of negative correlations include those between exercise and heart failure, between successful test performance and feelings of incompetence, and between absence from school and school achievement.

56. No CORRELATION Correlation Coefficient = -.16

57. 8.2 Scatter Plots Aus. Book Q. 3

58. Q. 4

59. Q. 7

60. Using your calculator to calculate the C.C!

61. Correlation Coefficient Before doing this on the calculator, the class should do a scatter graph using the data in the table. Discuss the relationship between the data (i.e. gms of fat v calories). Project Maths Development Team © 2008 Total Fat (g) Total Calories Hamburger 9 260 Cheeseburger 13 320 Quarter Pounder 21 420 Quarter Pounder with Cheese 30 530 Big Mac 31 560 Special 31 550 Special with Bacon 34 590 Crispy Chicken 25 500 Fish Fillet 28 560 Grilled Chicken 20 440 Grilled Chicken Light 5 300

63. SHARP EL-W531 Mode 1 1 2 (x,y) 5 DATA 12 (x,y) 24 DATA 21 (x,y) 24 DATA 15 (x,y) 25 DATA RCL r x y 2 2 12 21 21 21 15 5 5 24 40 40 40 25

64. Correlation Coefficient by Calculator This will show the table on the right on the screen. When all the data items are inputted, press the following: This will give a correlatrion coefficient of 0.9746 Compare this answer with your interpretation of the scatter graph. Using the Casio fx-83ES Project Maths Development Team © 2008 Now input all the data items into the X and Y columns. Press after each data item.

65. Scatter Plot of cricket chirps versus outdoor temperature.

66. Correlation of 0.98!

67. Correlation versus Causation

68. The amount of fuel burned by a car depends on the size of its engine, since bigger engines burn more petrol. We say there is a CASUAL RELATIONSHIP between the amount of petrol used and the size of the cars engine.

69. If two variables are found to be either associated or correlated, that doesn’t necessarily mean that a cause-and-effect relationship exists between the two variables. If we find a statistical relationship between two variables, then we cannot always conclude that one of the variables is the cause of the other, i.e. correlation does not always imply causality.

70. During 1980 and 2000 there was a large increase in sales of calculators and computers! There was a strong positive correlation between the sales of computers and the sales of calculators! For Example.. Did the increase of sales of calculators cause an increase in the sale of computers??

71. NO!!!! Production Costs Decreased Cost of Production was a third variable causing the other two to increase. We call this third variable a LURKING VARIABLE.

72. Linear Regression Line of Best Fit

73. After you’ve found a relationship between two variables and you have some way of quantifying this relationship, you can create a model that allows you to use one variabe to predict another.

74. 1. Draw a Scatter Plot. 2. If graph suggests a linear relationship.. 3. Calculate Correlation Coefficient. 4. Find the equation of the Line that best fits the data. - We draw this by eye, and then find its equation.

75. Because you have a strong correlation be it positive or negative you know that x is correlated with y. If you know the slope and the y-intercept of that line, then you can plug in a value for x and predict the average value for y. In other words, you can predict y from x. You should never do a regression analysis unless you’ve already found a strong correlation (either pos. or neg.) between the two variables!

76. Drawing by Eye Draw the line so there are roughly equal points above and below the line.

77. Drawing by Eye Two Draw a vertical line that splits the points up into two equal sized groups. If there are an odd number of points (for instance 5), just split the groups slightly unevenly (3 in one, 2 in the other). Find the middle of each group in the horizontal direction. Find the middle of each group in the vertical direction.

78. Draw a cross or marker at the midpoint of each of the two groups. The midpoint is the location found in steps 2 and 3. Draw a line between these two midpoints.

79. Step 1

80. Step 2

81. Step 3

82. Step 4

83. Step 5

84. Now Calculate Line! i.e. what is the formula for the line? i.e. what is the formula for the line?

85. Equation: y = mx + c M = slope y2-y2/x2-x1 where (x1,y1) and (x2,y2) are points on the line of best fit. Substitute the m and one point into y-y1=m(x-x1).

86. Q. 3 AQA GSCE

87. Q. 5

88. Q. 6

89. Q. 9 Active Maths 0.98

90. Q. 10 0.90

91. Exercise 1.7 QUESTION 4 (ii)0.96 (iii) Strong Positive Correlation (v) y = 4x + 6 (vi) € 18, 000

93. Q. 5 (ii) 1.00 (iv) Perfect positive correlation (v) y = 11/7 (x-51/7)

95. Q. 6 (ii) 0.99 (iii)Near - perfect positive correlation (v) y = 2.5 x + 14 (vi) 39 %

96. Let’s Sum up! Types of Sampling Populations and Samples Types of Sampling Bias in Sampling Reliability of Data Collecting Data

97. Frequency Tables Stem-and-Leaf Diagram Back-toBack S & L Histograms Distribution of Data

98. Scatter Graph Correlation Correlation Coefficent Causality Linear Regression