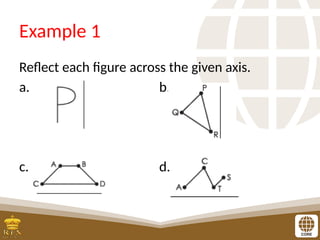
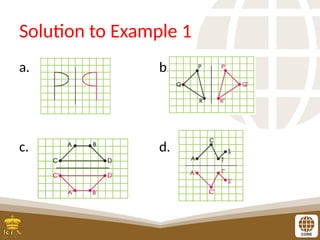
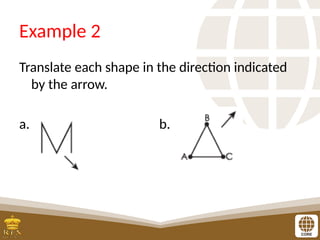
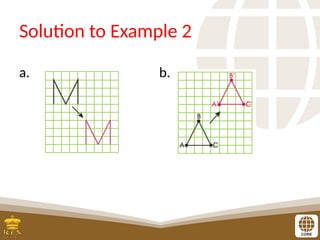
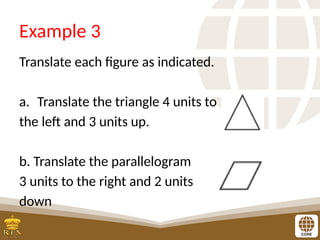
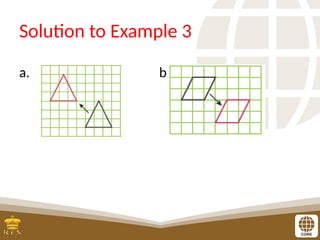
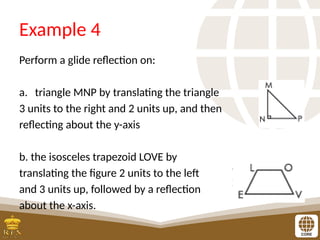
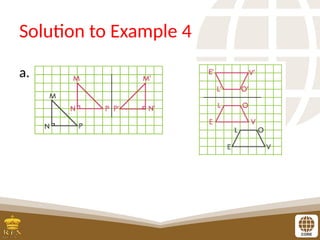
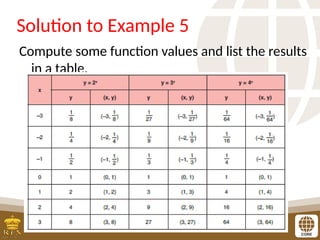
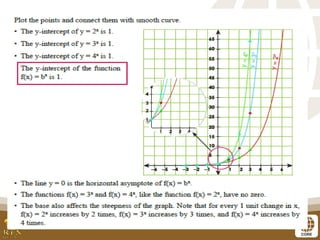
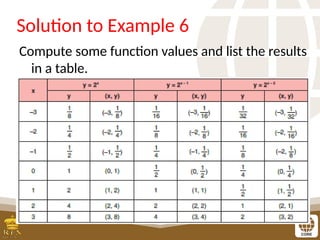
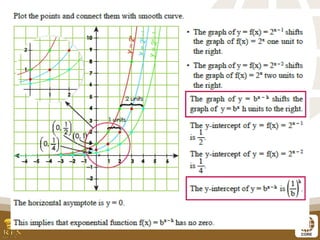
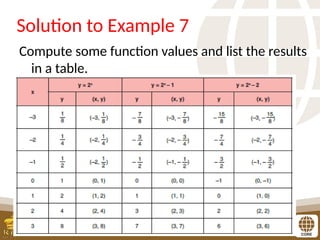
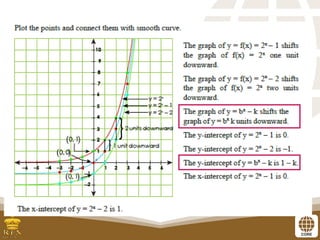
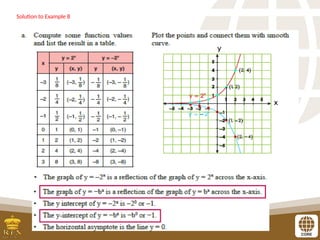
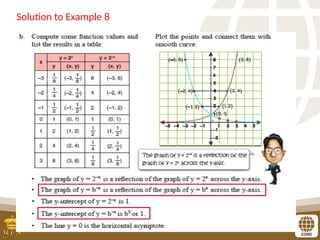
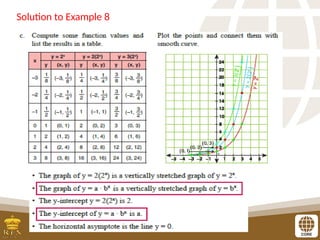
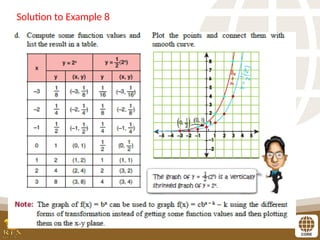
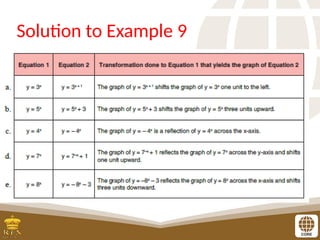
The document covers the teaching of exponential functions, including their representation through tables, graphs, and equations, as well as the characteristics such as domain, range, and asymptotes. It also discusses transformations of shapes, including reflections and translations, and how to graph various exponential functions. Examples and exercises are provided to reinforce understanding of the concepts presented.

1. Exponential Functions
General Mathematics
O. Oronce

2. Lesson Objectives
At the end of the lesson, the students must be able
to:
• represent an exponential function through its: (a)
table of values, (b) graph, and (c) equation;
• find the domain and range of an exponential
function;
• find the intercept, zeros, and asymptote of an
exponential function; and
• graph exponential functions.

3. Zero as an Exponent
• If a ≠ 0, then a⁰ = 1
Illustration:
To evaluate 3⁰ 3², we have
∙
3⁰ 3² = 3⁰⁺² = 3² = 9 or
∙
3⁰ 3² = 1 3² = 1 9 = 9
∙ ∙ ∙

4. Negative Exponent
• If n is any integer, and a and b are not equal to
zero, then
• Illustration
Note: The negative exponent does not make the
answer negative
n
n
n
n
n
a
b
b
a
and
a
a
a 





















 1
1
8
1
2
1
2 3
3

 


5. Definition
Transformation – the process of moving a figure
from the starting position to some ending
position without changing its size and shape.
Reflection – a transformation that produces a
new figure, which is a mirror image of the
original figure.

6. Definition
Translation – a shift or movement in a figure’s
location without changing its shape.
Glide Reflection – a combination of a reflection
and a translation (glide).

7. Example 1
Reflect each figure across the given axis.
a. b.
c. d.

8. Solution to Example 1
a. b.
c. d.

9. Example 2
Translate each shape in the direction indicated
by the arrow.
a. b.

10. Solution to Example 2
a. b.

11. Example 3
Translate each figure as indicated.
a. Translate the triangle 4 units to
the left and 3 units up.
b. Translate the parallelogram
3 units to the right and 2 units
down

12. Solution to Example 3
a. b.

13. Example 4
Perform a glide reflection on:
a. triangle MNP by translating the triangle
3 units to the right and 2 units up, and then
reflecting about the y-axis
b. the isosceles trapezoid LOVE by
translating the figure 2 units to the left
and 3 units up, followed by a reflection
about the x-axis.

14. Solution to Example 4
a. b.

15. Exponential Function
An exponential function can be written as
f (x) = bˣ
where b > 0, b ≠ 1, and x is any real number
In the equation f(x) = bˣ, b is a constant called
the base and x is an independent variable
called the exponent.

16. Here are some examples of exponential
functions.
The following are not exponential functions.

17. Properties of Exponential Functions and
Their Graphs
Let f(x) = bˣ, b > 1, and b ≠ 1.
1. The domain is the set of real numbers, (-∞, ∞).
2. The range is the set of positive real numbers, (0, ∞).
3. If b > 1, f is an increasing exponential function. If 0 <
b < 1, f is a decreasing exponential function
4. The function passes through the point (0,1) because
f(0) = b⁰ = 1.
5. The graph approaches but does not reach the x-axis.
The x-axis is the horizontal asymptote.

18. Example 5
Sketch the graph of y = 2ˣ, y = 3ˣ, and y = 4ˣ in
one plane. Describe the significance of the
constant b in the equation y = bˣ

19. Solution to Example 5
Compute some function values and list the results
in a table.

21. Example 6
Sketch the graph of y = 2ˣ, y = 2ˣ⁻¹ in one plane.
Describe the graph

22. Solution to Example 6
Compute some function values and list the results
in a table.

24. Example 7
Sketch the graph of y = 2ˣ, y = 2ˣ-1, and y = 2ˣ - 2
in one plane.
Describe the graphs.

25. Solution to Example 7
Compute some function values and list the results
in a table.

27. Example 8
Graph each group of functions in one plane.
Describe the graphs.
a. y = 2ˣ and y = -2ˣ
b. y = 2ˣ and y = 2⁻ˣ
c. y = 2ˣ, y = 2 (2ˣ), and y = 3(2ˣ)
d. y = 2ˣ and y = ½ (2ˣ)

28. Solution to Example 8

29. Solution to Example 8

30. Solution to Example 8

31. Solution to Example 8

32. Transformations Involving Exponential
Functions

33. Reflections in the Coordinate Axes
Reflections in the coordinate axes of the graph y
= f(x) are represented as follows:
1. Reflection in the x-axis: f(x) = -f(x)
2. Reflection in the y-axis: f(x) = f(-x)

34. Example 9
Use equation 1 to describe the transformation
that yields the graph of equation 2.

35. Solution to Example 9

36. Exercise A
Evaluate the following for the indicated value(s) of x.
1. f(x) = 3x; x = 1, x =
2. f(x) = 4 - 3x; x = 4, x =
3. g(x) = 3ˣ; x = , x = 4
4. h(x) = ; x = , x = -1
5. f(x) = 3ˣ⁻¹; x = 2, x = -2
3
1
2
1
x
2
3
1






2
1
2
1

37. Exercise B
Make a table of coordinates then graph each
function.
1. f(x) = 5ˣ 6. g(x) = 4⁻ˣ⁺²
2. f(x) = 6⁻ˣ 7. h(x) =
3. g(x) = -5ˣ
4. f(x) = 3ˣ⁻² 8. f(x) =
5. f(x) =
1
2
1








x
x






3
2
x






3
1

38. Exercise C
Find the base of the exponential function whose
graph contains the given points.
1. (2, 16) 5. (4, )
2. (1, 10)
3. (3, 64) 6. ( , 27)
4. (3, )
343
1
625
1
2
3