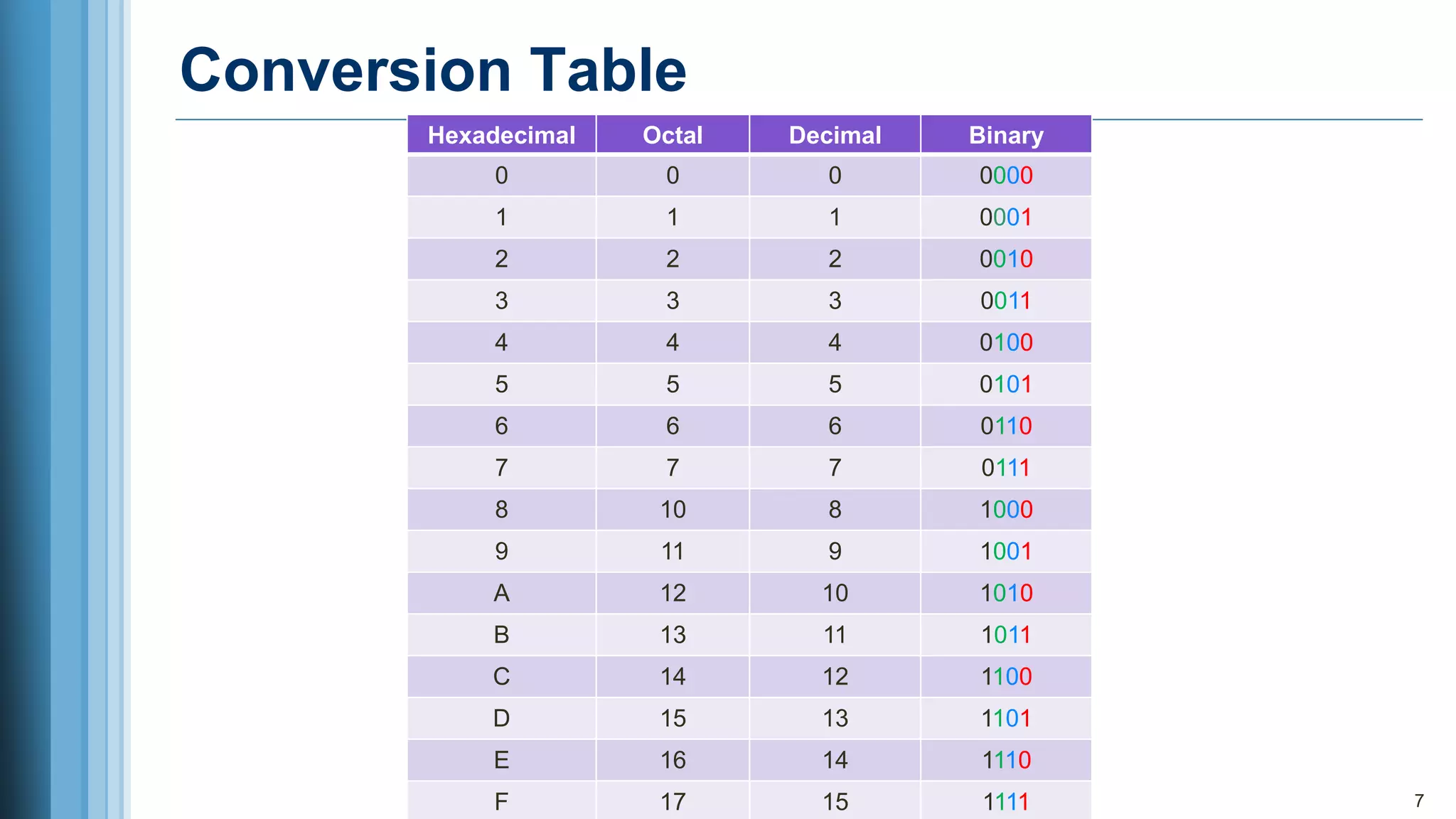
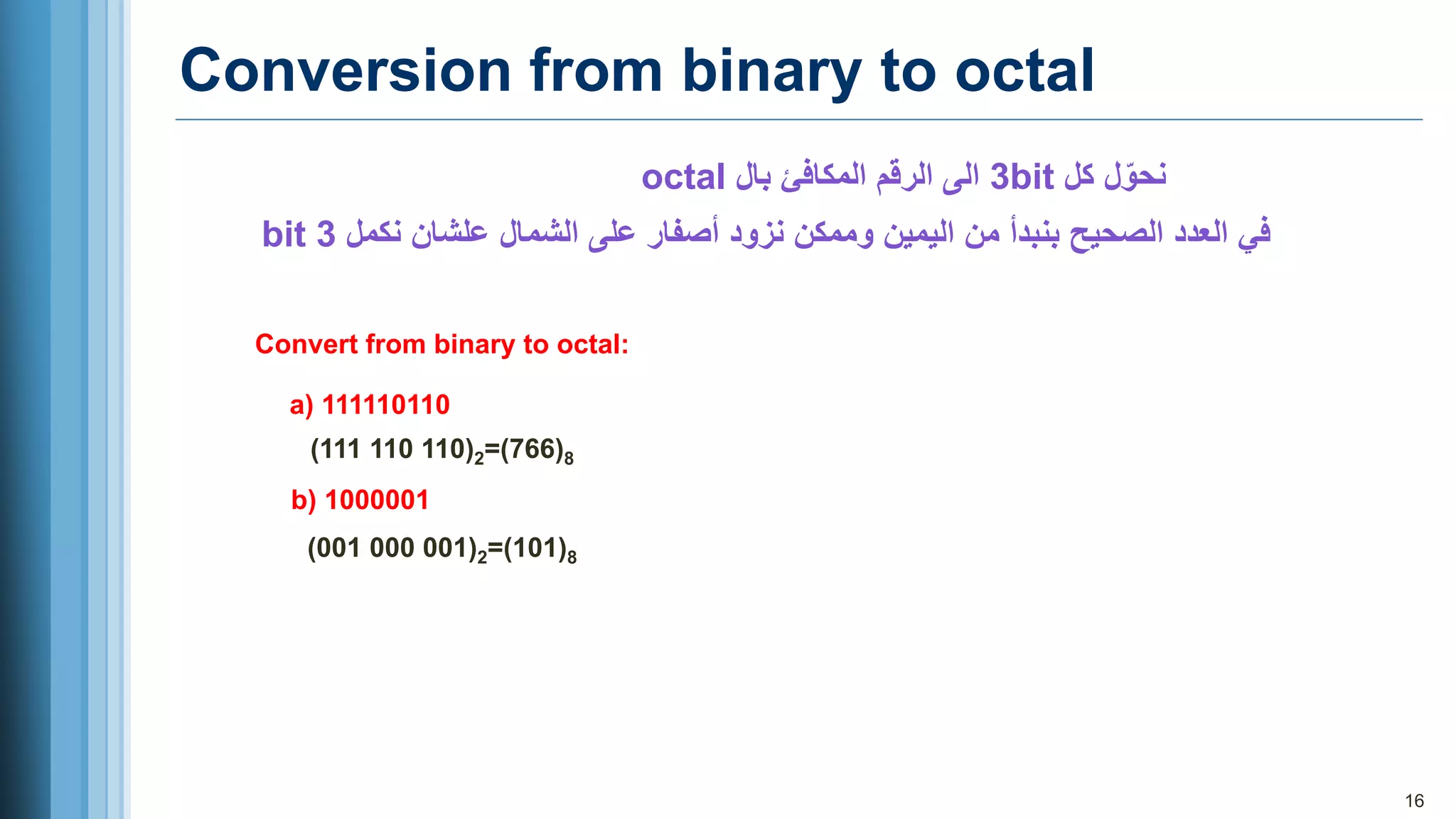
This document provides an overview of numerical analysis and number systems. It discusses: 1. Assessment criteria for the course including exams, assignments, and participation. 2. An introduction to numbers, digits, and different number systems like binary, octal, decimal, and hexadecimal. 3. Methods for converting between number systems including decimal to other bases, other bases to decimal, and shortcuts for binary, octal, and hexadecimal conversions.

1. 1
Numerical Analysis
Lecture 1

2. Assessment
2
Total: 100 marks
• Final Exam: 60 marks
• Mid-term: 15 marks
• Oral : 10 marks
• Assignments: 10 marks
• Participation: 5 marks
You will pass if you get 50 marks (PASS)

3. Assignments
• Google Classroom
• Code:
3
x3n5el6

4. Numbers
4
• A number is a mathematical object used to count, measure, and
label.
• Numbers can be represented in languages with symbols.
e.g.:

5. Digits and Numbers
• Digit
A digit is a single numerical symbol.
For example: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9.
• Number
A number is a string of one or more digits.
For example, the number 23 is written with two digits, 2 and 3.
5

6. Number Systems
6
System Digits Base
Binary 0,1 Base-2
Octal 0,1,2,3,4,5,6,7 Base-8
Decimal 0,1,2,3,4,5,6,7,8,9 Base-10
Hexadecimal 0,1,2,3,4,5,6,7,8,9,A,B,C,D,E,F Base-16

7. Conversion Table
7
Hexadecimal Octal Decimal Binary
0 0 0 0000
1 1 1 0001
2 2 2 0010
3 3 3 0011
4 4 4 0100
5 5 5 0101
6 6 6 0110
7 7 7 0111
8 10 8 1000
9 11 9 1001
A 12 10 1010
B 13 11 1011
C 14 12 1100
D 15 13 1101
E 16 14 1110
F 17 15 1111

8. Conversions
• Decimal to Other Base System
• Other Base System to Decimal
• Other Base System to Non-Decimal
• Shortcut method − Binary to Octal
• Shortcut method − Octal to Binary
• Shortcut method − Binary to Hexadecimal
• Shortcut method − Hexadecimal to Binary
8
We'll demonstrate here the following:

9. Decimal to Other Base System
• Step 1 − Divide the decimal number to be converted by the value of the
new base.
• Step 2 − Get the remainder from Step 1 as the rightmost digit (least
significant digit) of new base number.
• Step 3 − Divide the quotient of the previous divide by the new base.
• Step 4 − Record the remainder from Step 3 as the next digit (to the left) of
the new base number.
Repeat Steps 3 and 4, getting remainders from right to left, until the quotient
becomes zero in Step 3.
9
Steps:

10. Conversion from decimal to any base (Base-x)
10
❑ For integer number → divide by x
Example:
Convert from decimal to binary:
(45)10
45
2
22
1
2
11
2
5
2
2
2
1
2
0
0
1
1
0
1
101101
‫أعلى‬ ‫إلى‬ ‫أسفل‬ ‫من‬ ‫الرقم‬ ‫نكتب‬
(69)10
69
2
34
1
2
17
2
8
2
4
2
2
2
1
0
1
0
0
0
1000101
2
0
1
‫الباقي‬

11. Conversion from decimal to any base (Base-x)
11
Convert from decimal to octal:
901
901
8
112
5
8
14
0
8
1
6
8
0
1
1605
(901)10 → (1605)8

12. Conversion from decimal to any base (Base-x)
12
Convert from decimal to hexadecimal:
1066
1066
16
66
10
16
4
2
16
0
4
(1066)10 → (42A)16

13. 13
Conversion from any base (Base-x) to decimal
Result = SUM (value * xpos)
Example:
Convert from binary to decimal:
101011
1 0 1 0 1 1
 pos
5 4 3 2 1 0
= 1*20+1*21+0*22+1*23+0*24+1*25
=1+2+0+8+0+32
=43
 value
(101011)2 → (43)10

14. Conversion from any base (Base-x) to decimal
14
Convert from octal to decimal:
672
(672)8=2*80+7*81+6*82
=2+56+384
=(442)10
5061
(5561)8=1*80+6*81+0*82+5*83
=1+48+0+2560
=(2609)10

15. Conversion from octal to binary
15
Replace each octal digit into its equivalent 3-bit binary number
Convert from octal to binary:
(537)8
(537)8= (101 011 111)2

16. Conversion from binary to octal
16
‫كل‬ ‫ل‬ّ‫نحو‬
3bit
‫بال‬ ‫المكافئ‬ ‫الرقم‬ ‫الى‬
octal
Convert from binary to octal:
a) 111110110
(111 110 110)2=(766)8
b) 1000001
(001 000 001)2=(101)8
‫الصحيح‬ ‫العدد‬ ‫في‬
‫بنبدأ‬
‫الشمال‬ ‫على‬ ‫أصفار‬ ‫نزود‬ ‫وممكن‬ ‫اليمين‬ ‫من‬
‫علشان‬
‫نكمل‬
3
bit

17. Conversion from hexadecimal to binary
17
Replace each hexadecimal digit into its equivalent 4-bit binary number
Convert from hexadecimal to binary:
(A8C3)16
(A8C3)16= (1010 1000 1100 0011)2

18. 18
Conversion from binary to hexadecimal
‫كل‬ ‫ل‬ّ‫نحو‬
4bit
‫بال‬ ‫المكافئ‬ ‫الرقم‬ ‫الى‬
hexadecimal
‫الصحيح‬ ‫العدد‬ ‫في‬
‫بنبدأ‬
‫الشمال‬ ‫على‬ ‫أصفار‬ ‫نزود‬ ‫وممكن‬ ‫اليمين‬ ‫من‬
‫علشان‬
‫نكمل‬
4
bit
Convert from binary to hexadecimal:
a) 10101001
(1010 1001)2= (A9)16
d) 01101111
(0110 1111)2= (6F)16

19. Conversion from octal to hexadecimal
19
Octal → Binary → Hexadecimal
Convert from octal to hexadecimal:
A) 777
(777)8 → (111111111)2 → (0001 1111 1111)2 → (1FF)16
B) 605
(605)8 → (110000101)2 → (0001 1000 0101)2 → (185)16
C) 443
(443)8 → (100100011)2 → (0001 0010 0011)2 → (123)16

20. 20
Conversion from hexadecimal to octal
Hexadecimal → Binary → Octal
Convert from hexadecimal to octal:
A) A9
(A9)16=(10101001)2=(010 101 001)2=(251)8
B) E7
(E7)16=(11100111)2=(011 100 111)2=(347)8

21. 21