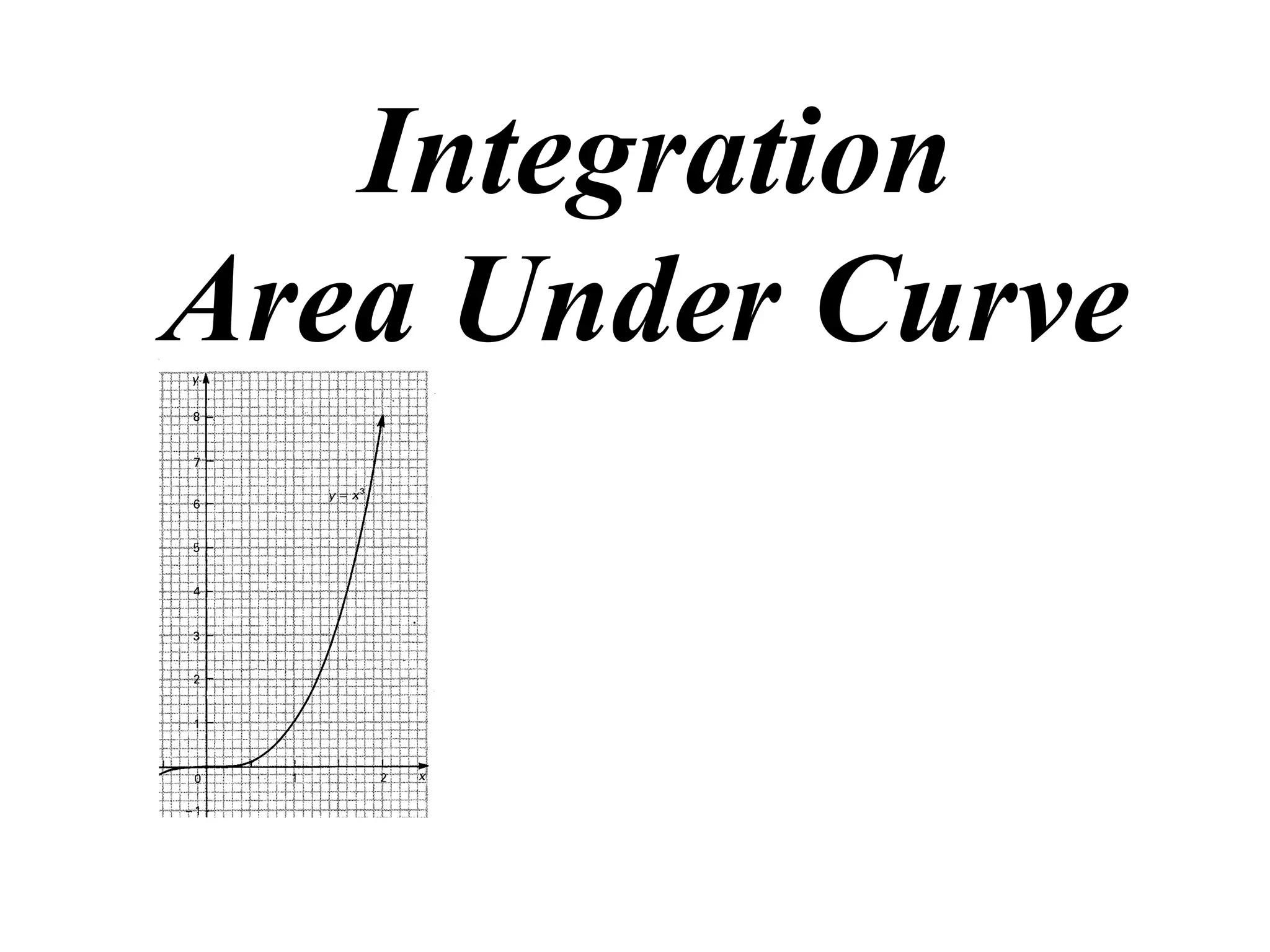
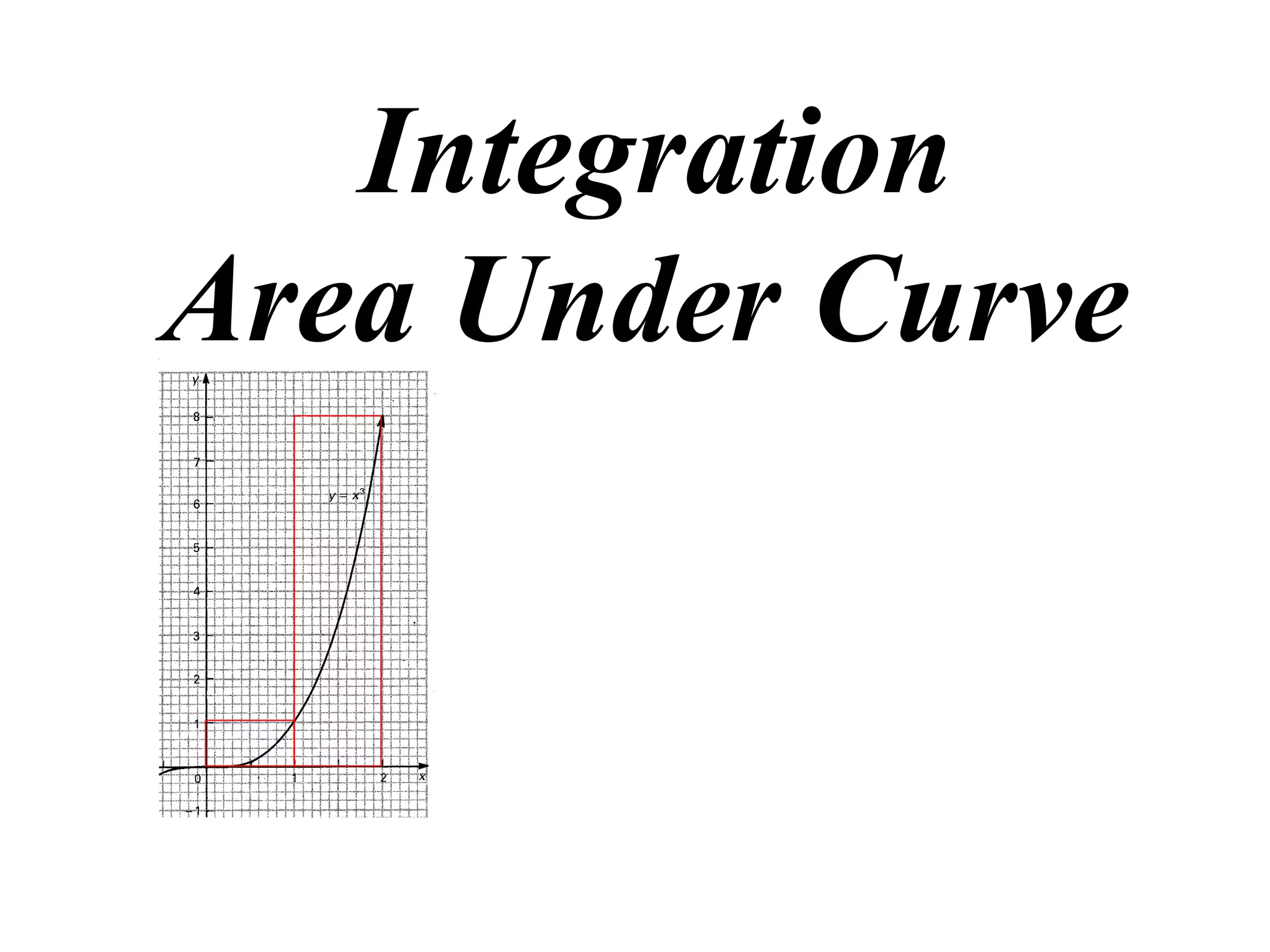
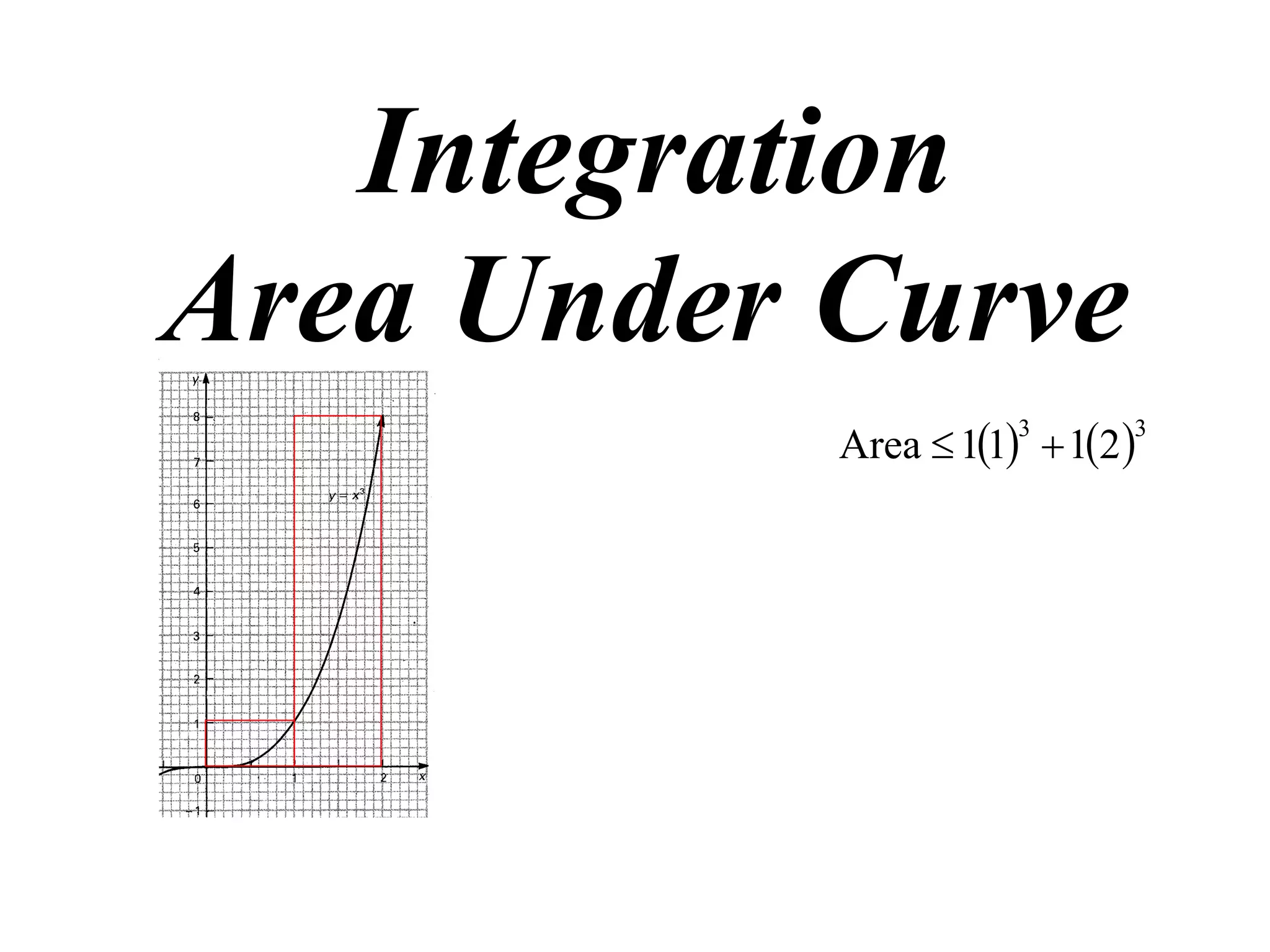
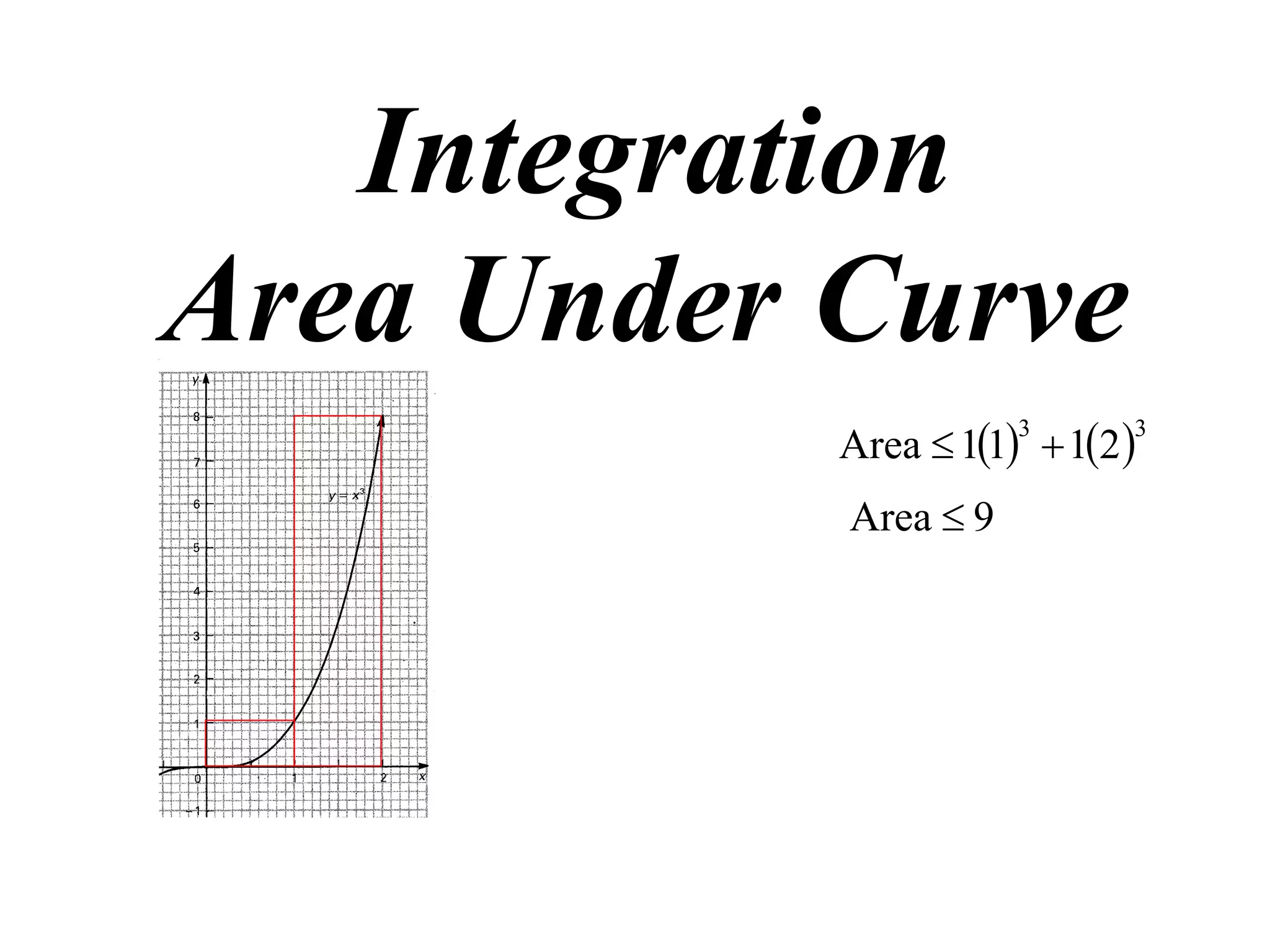
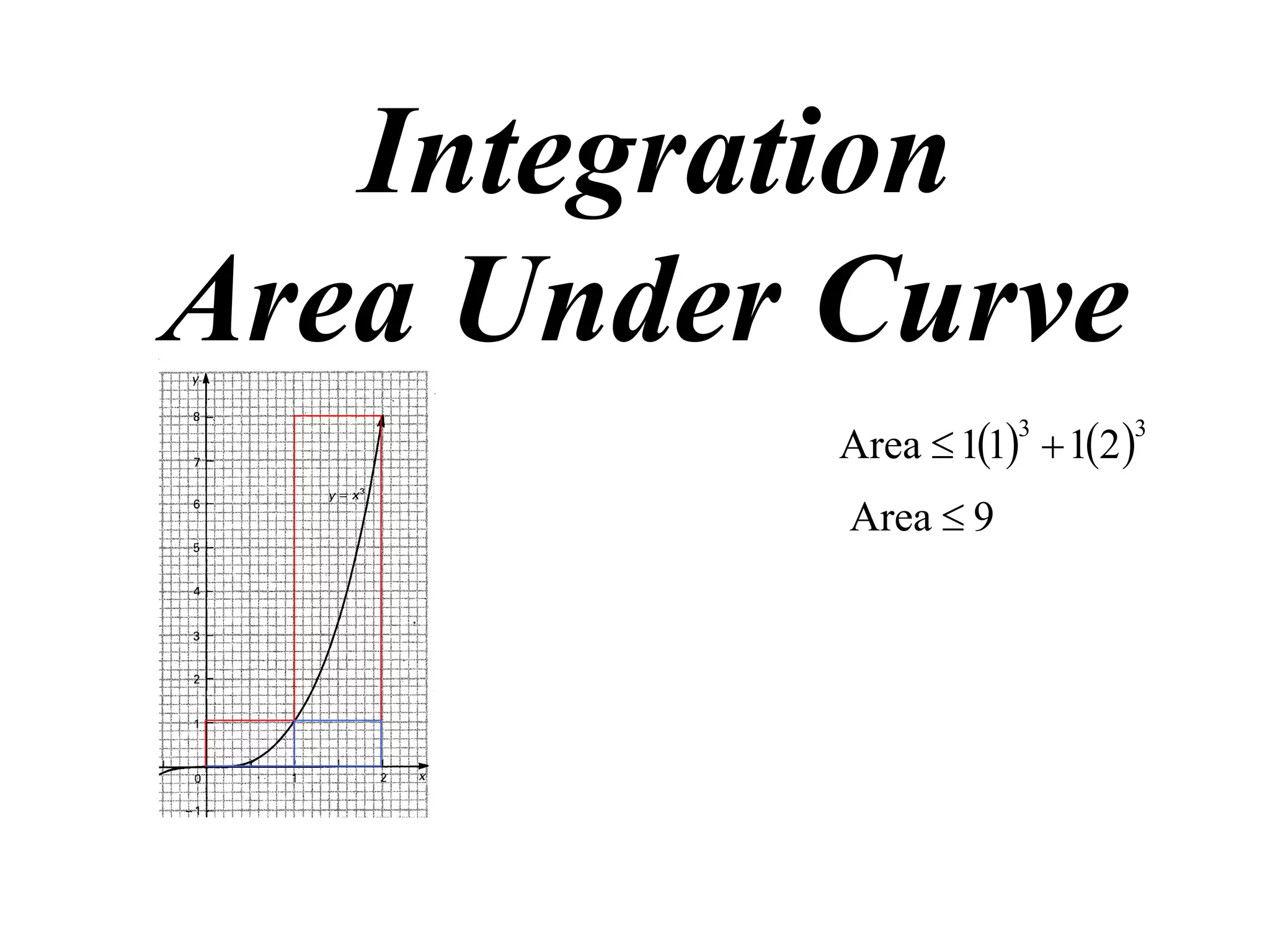
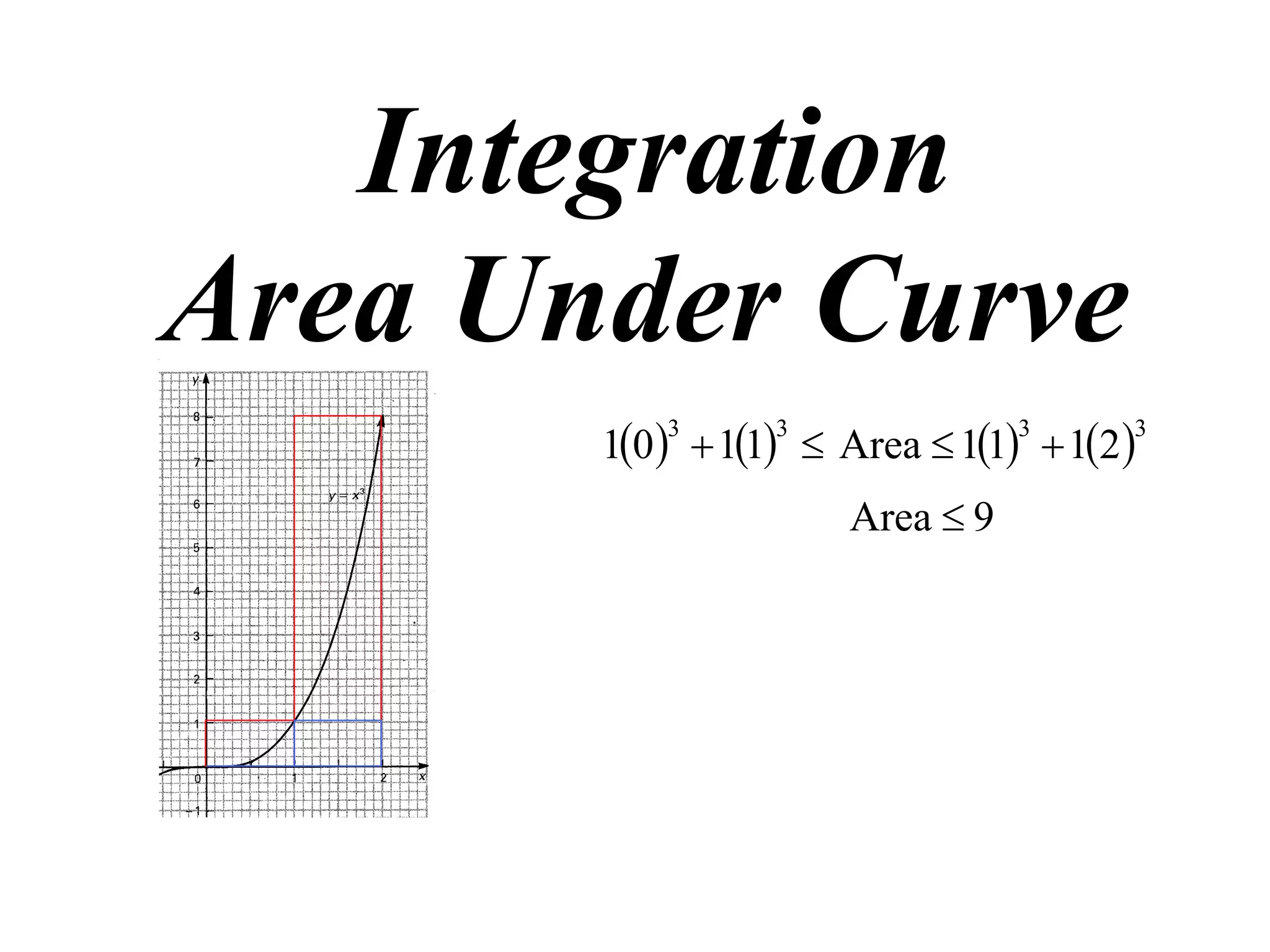
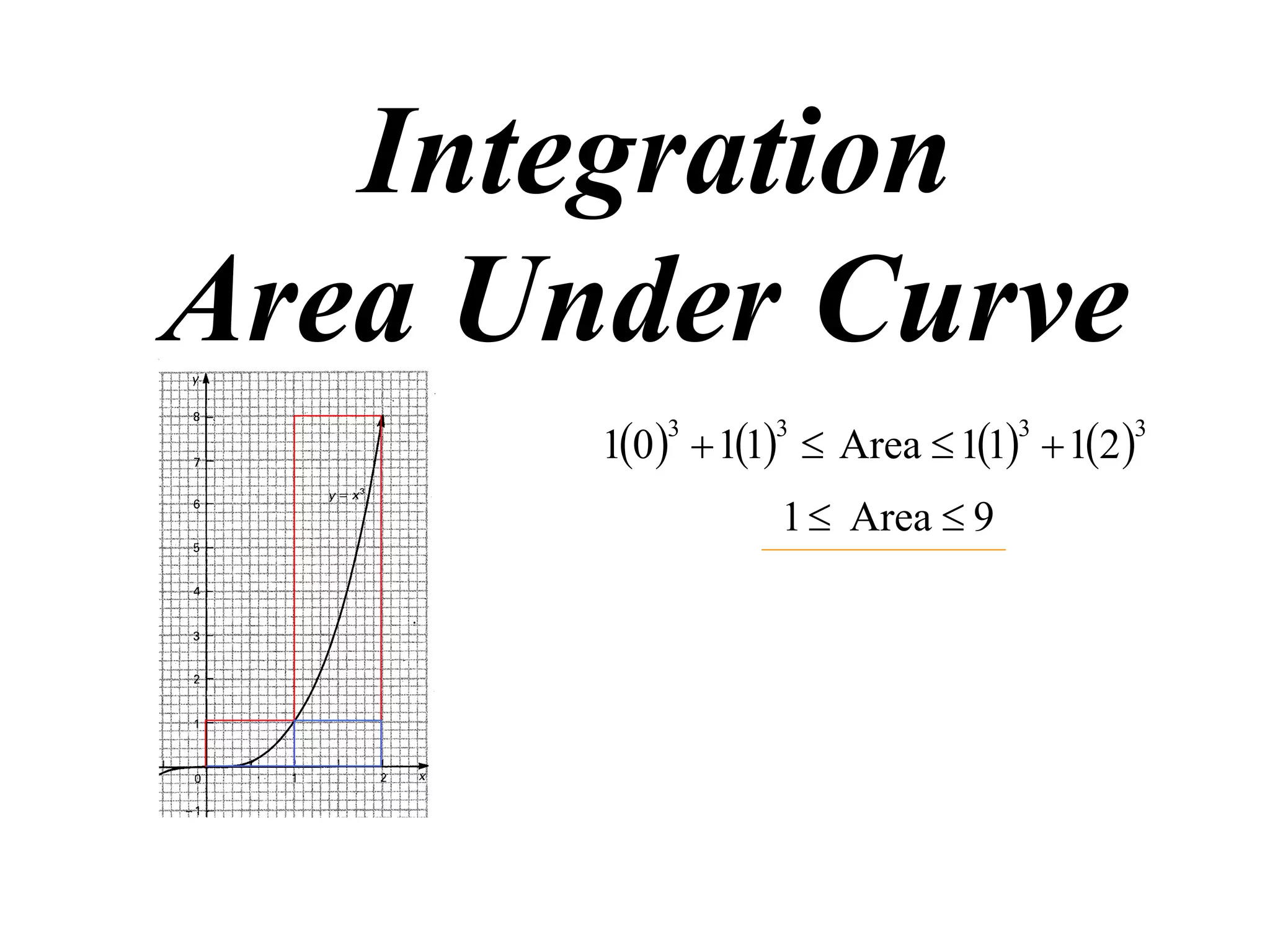
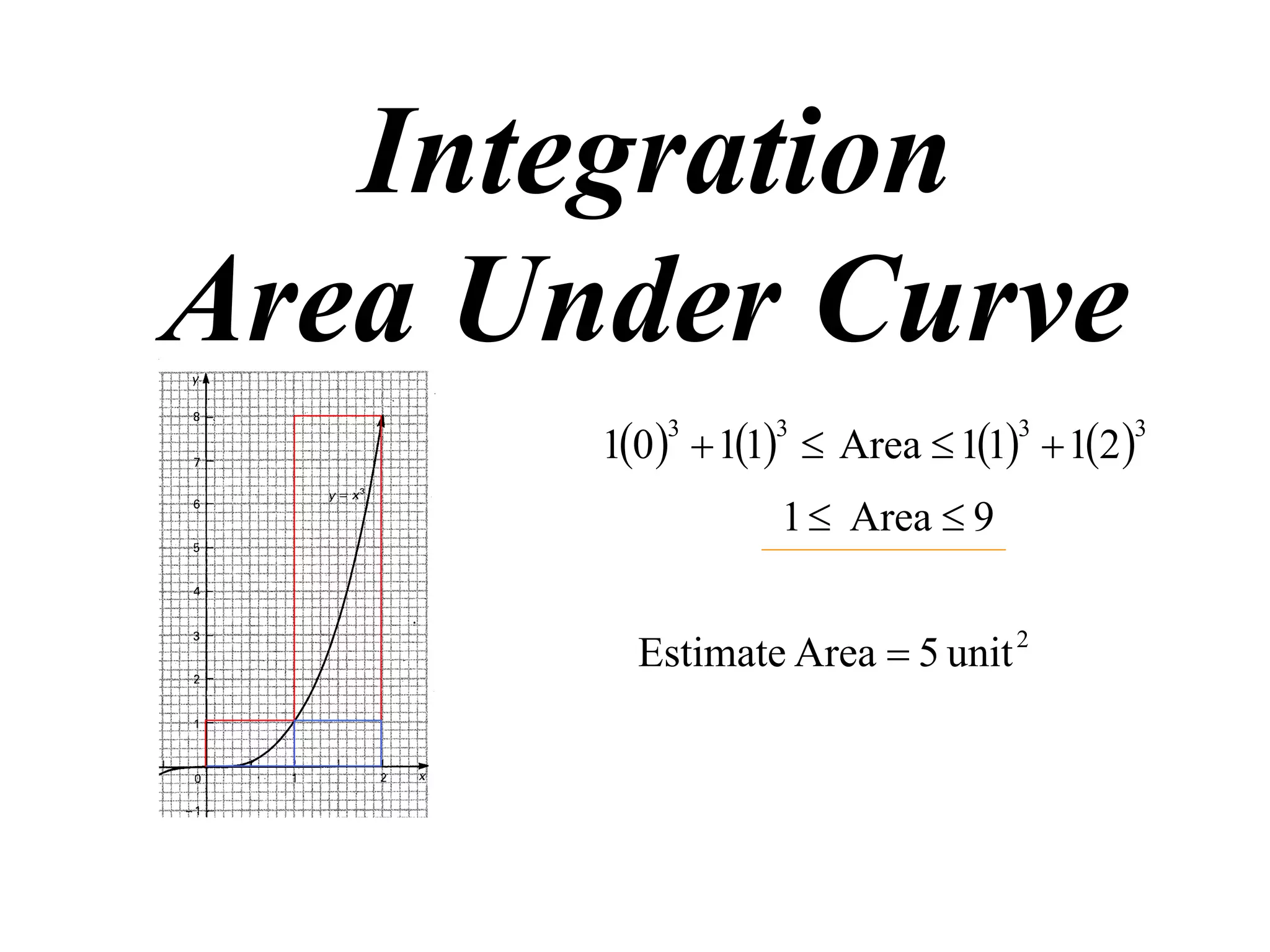
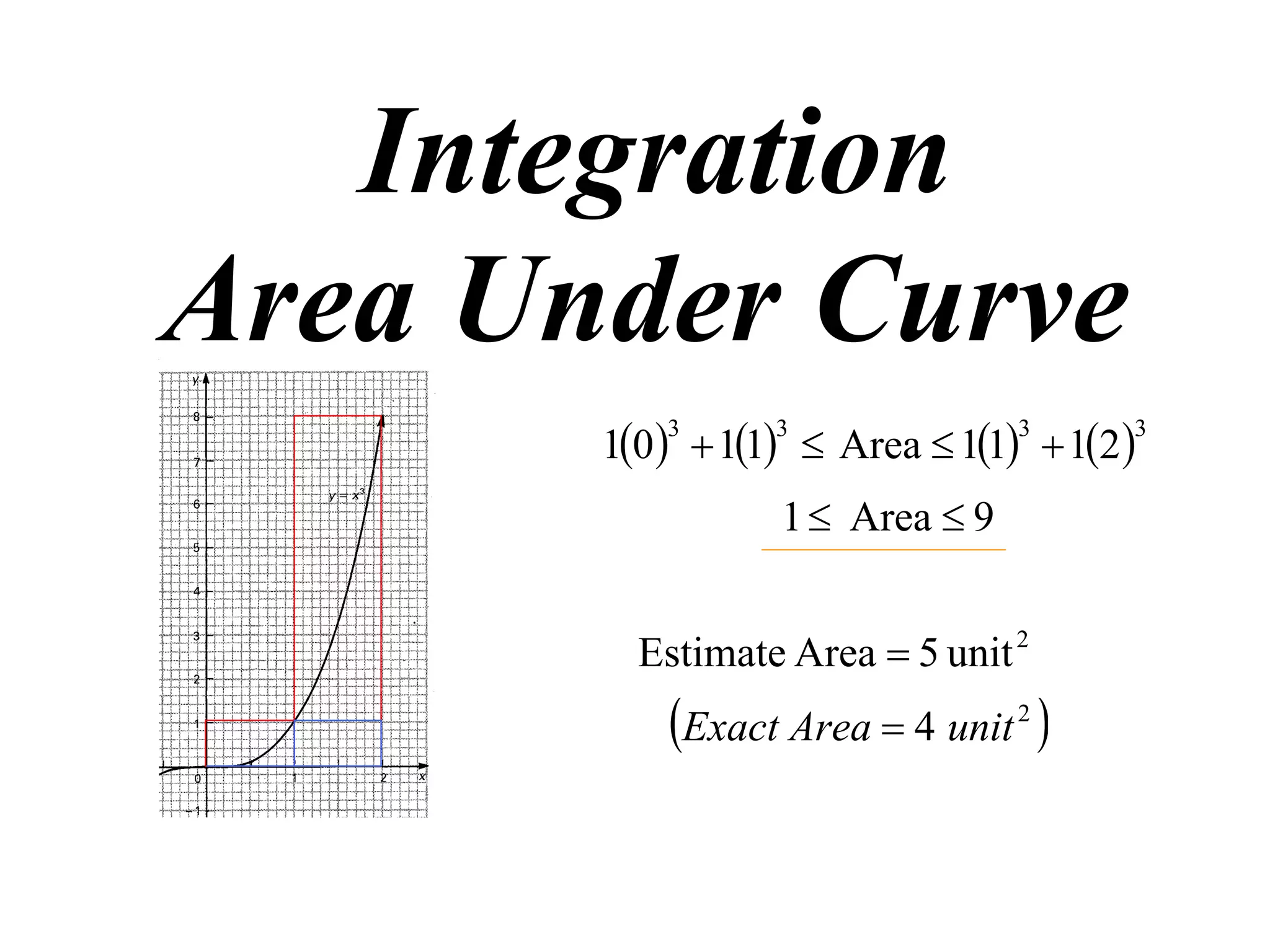
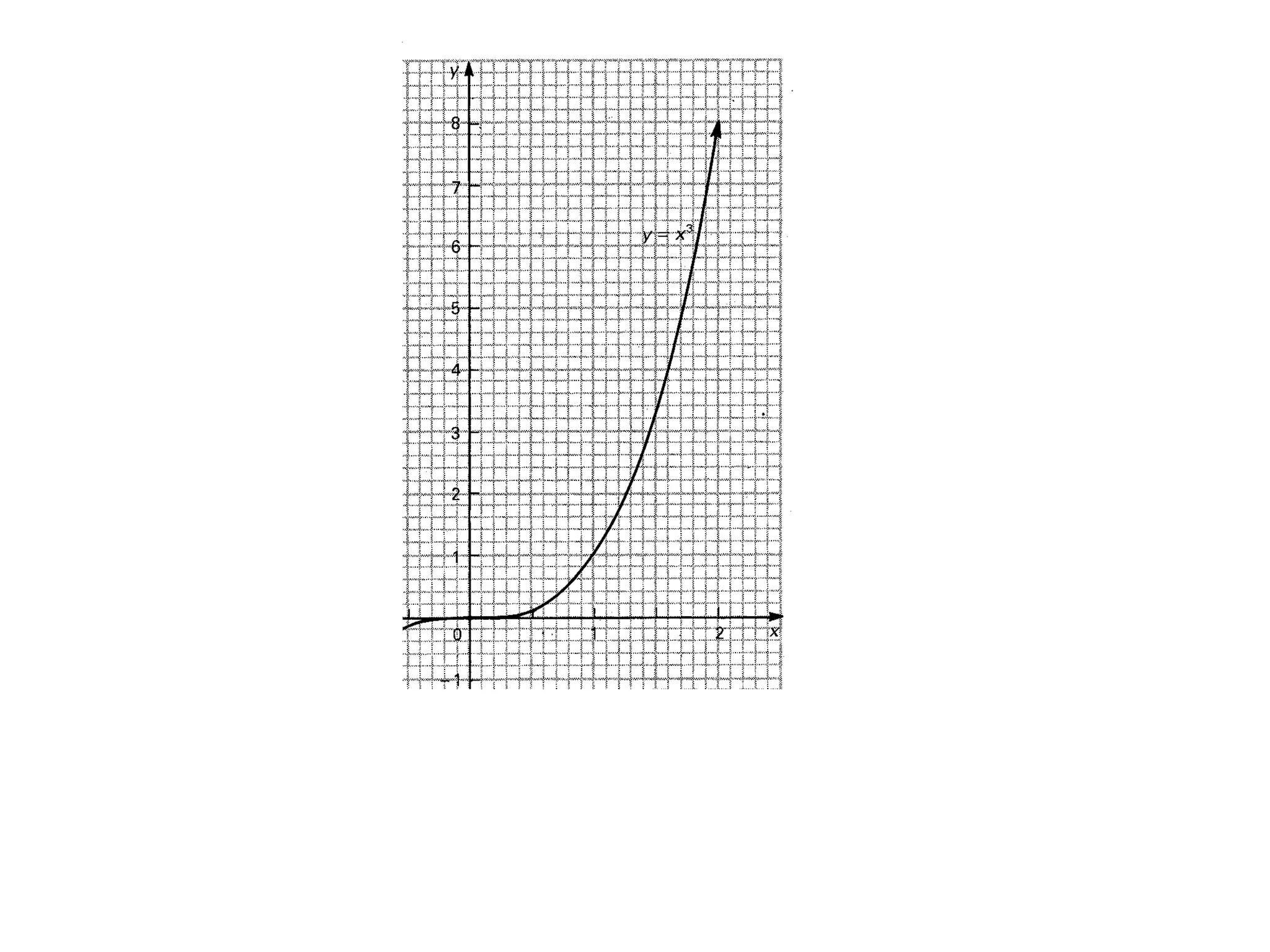
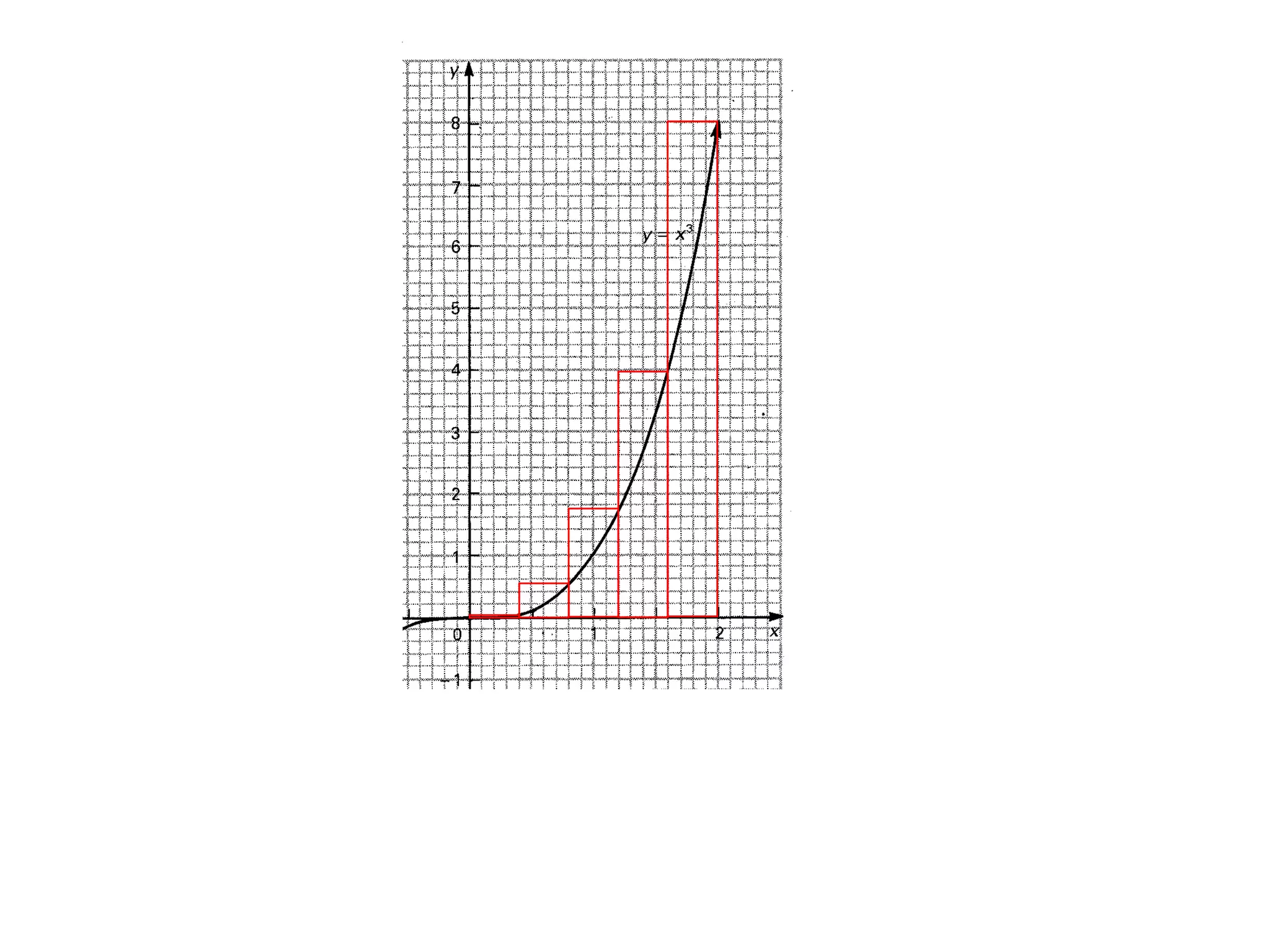
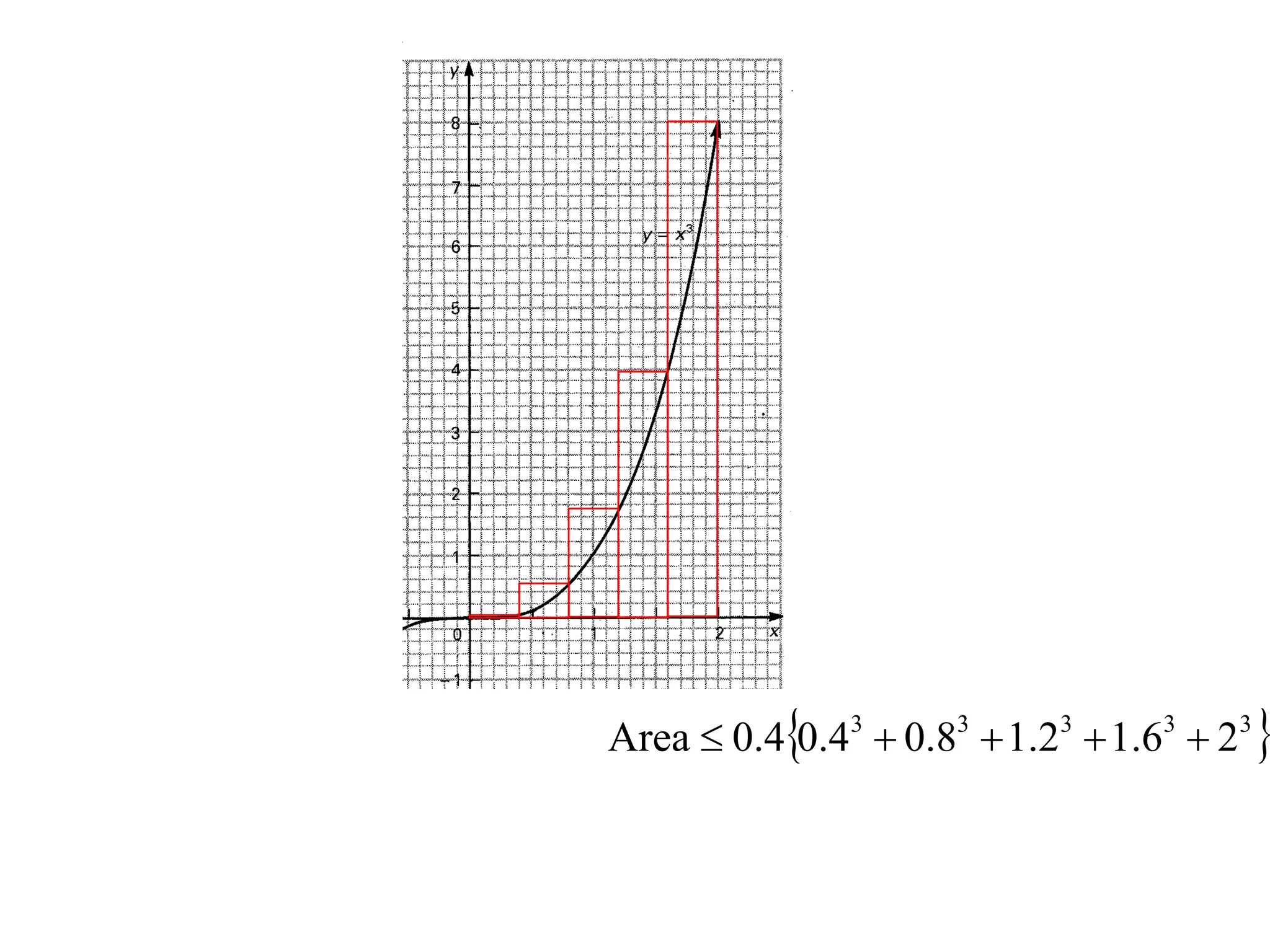
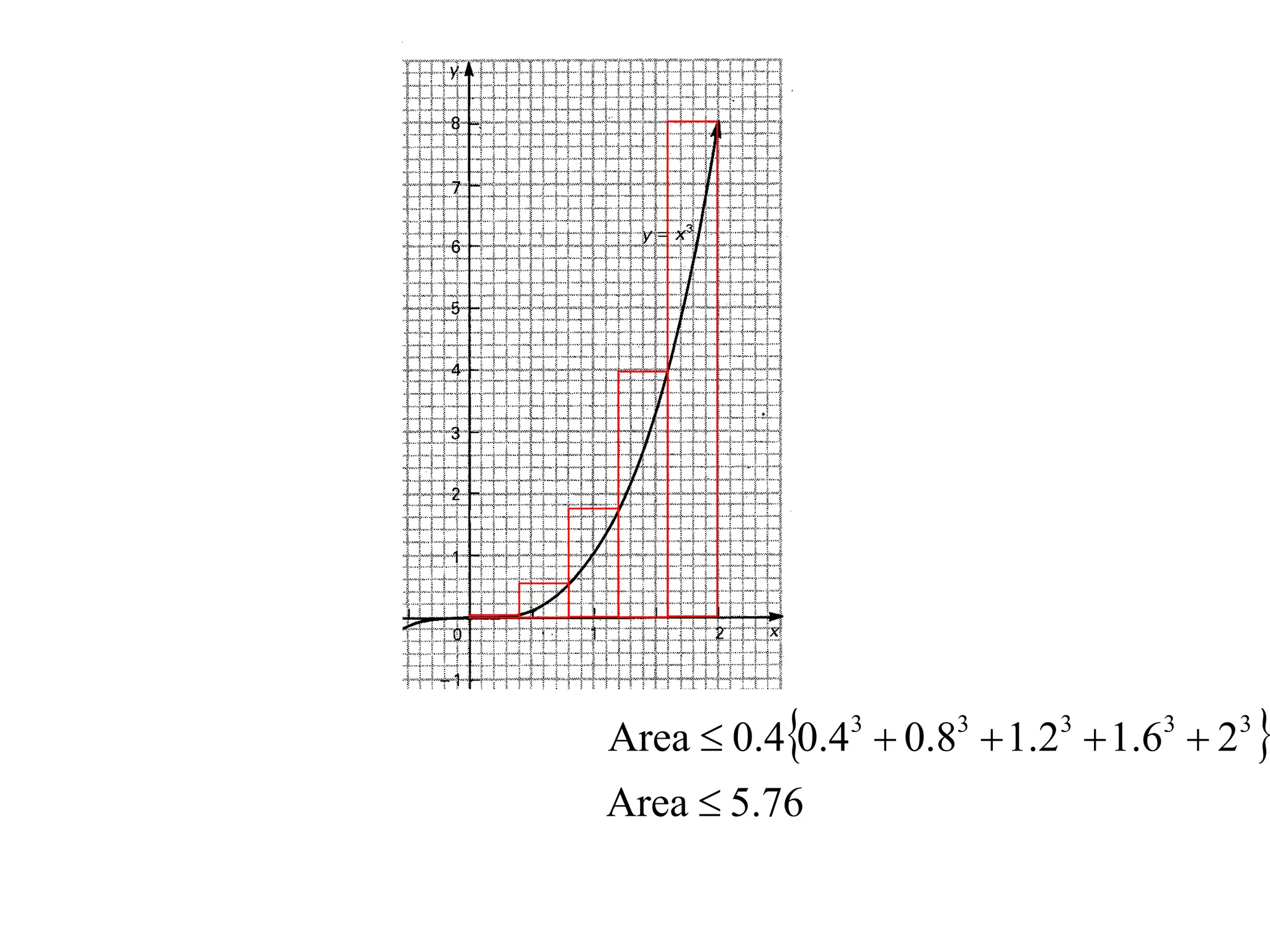
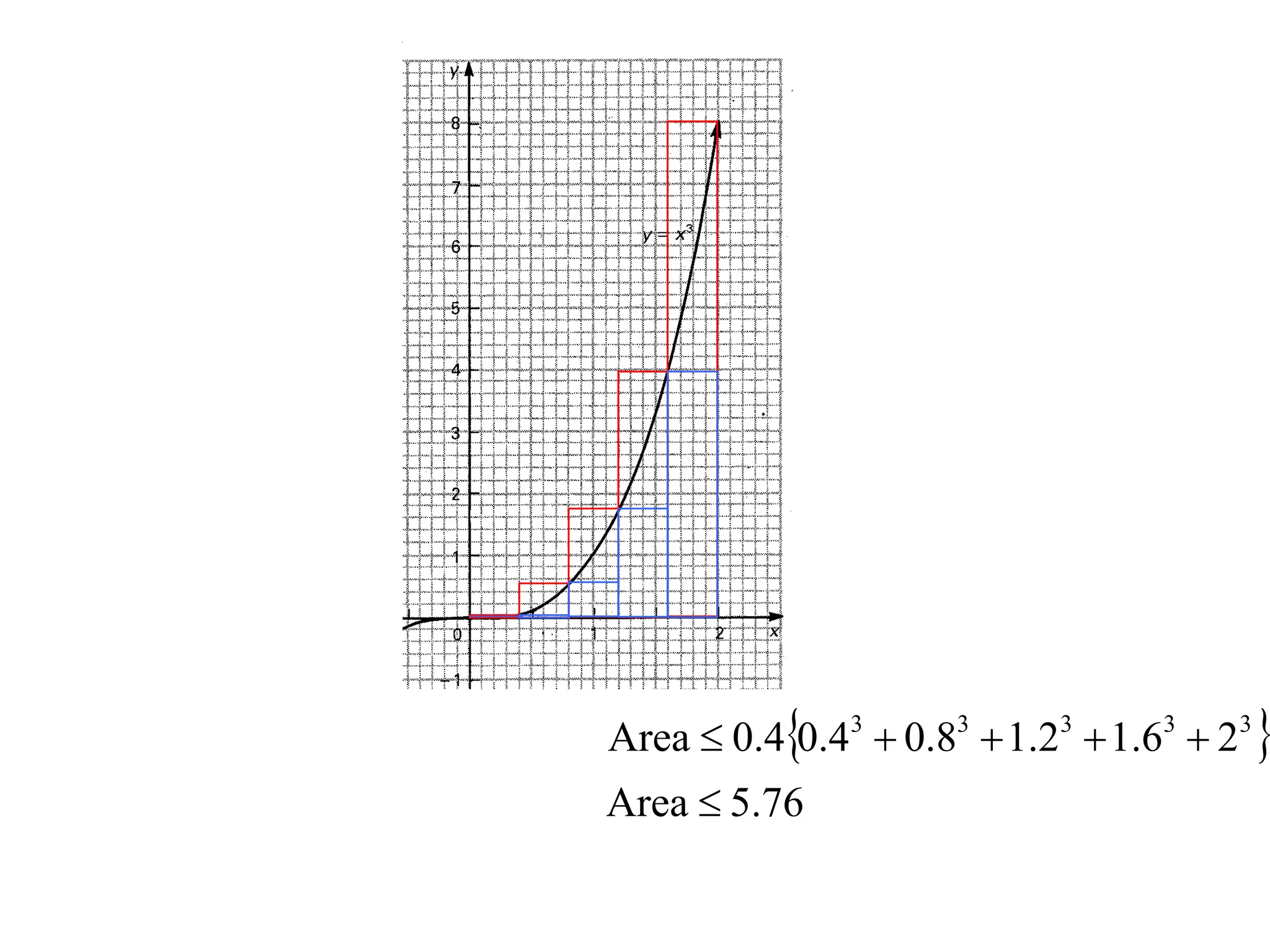
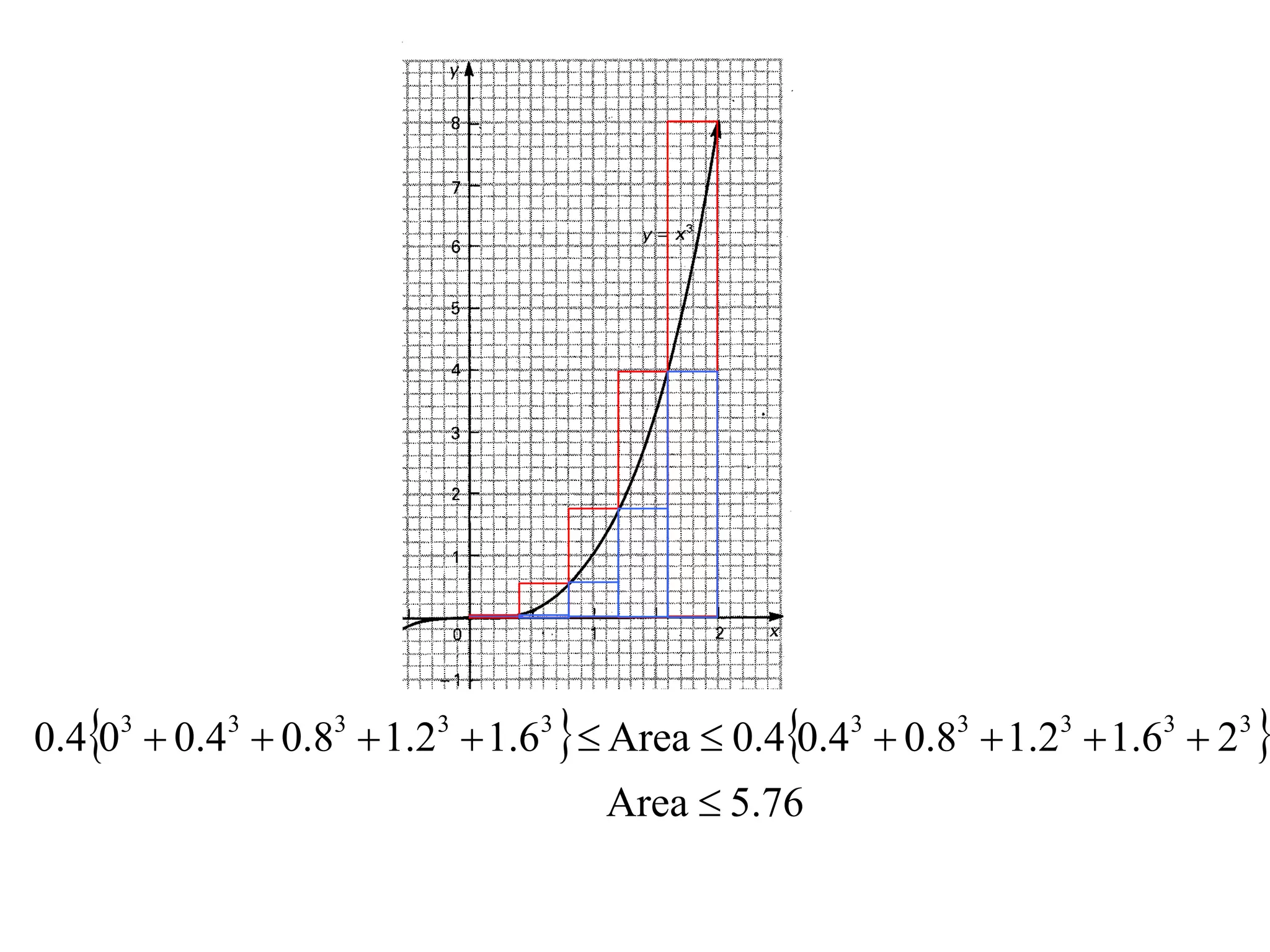
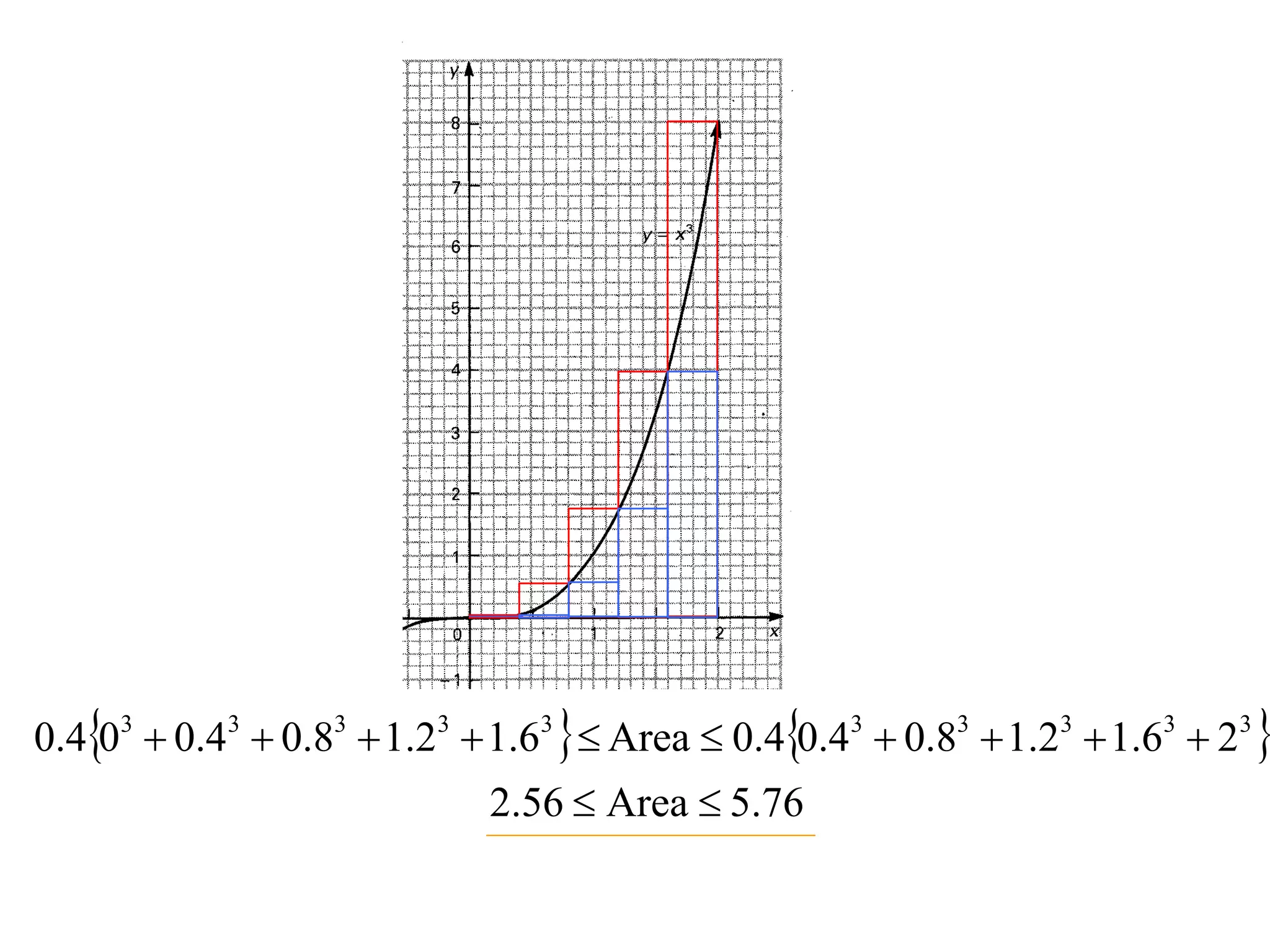
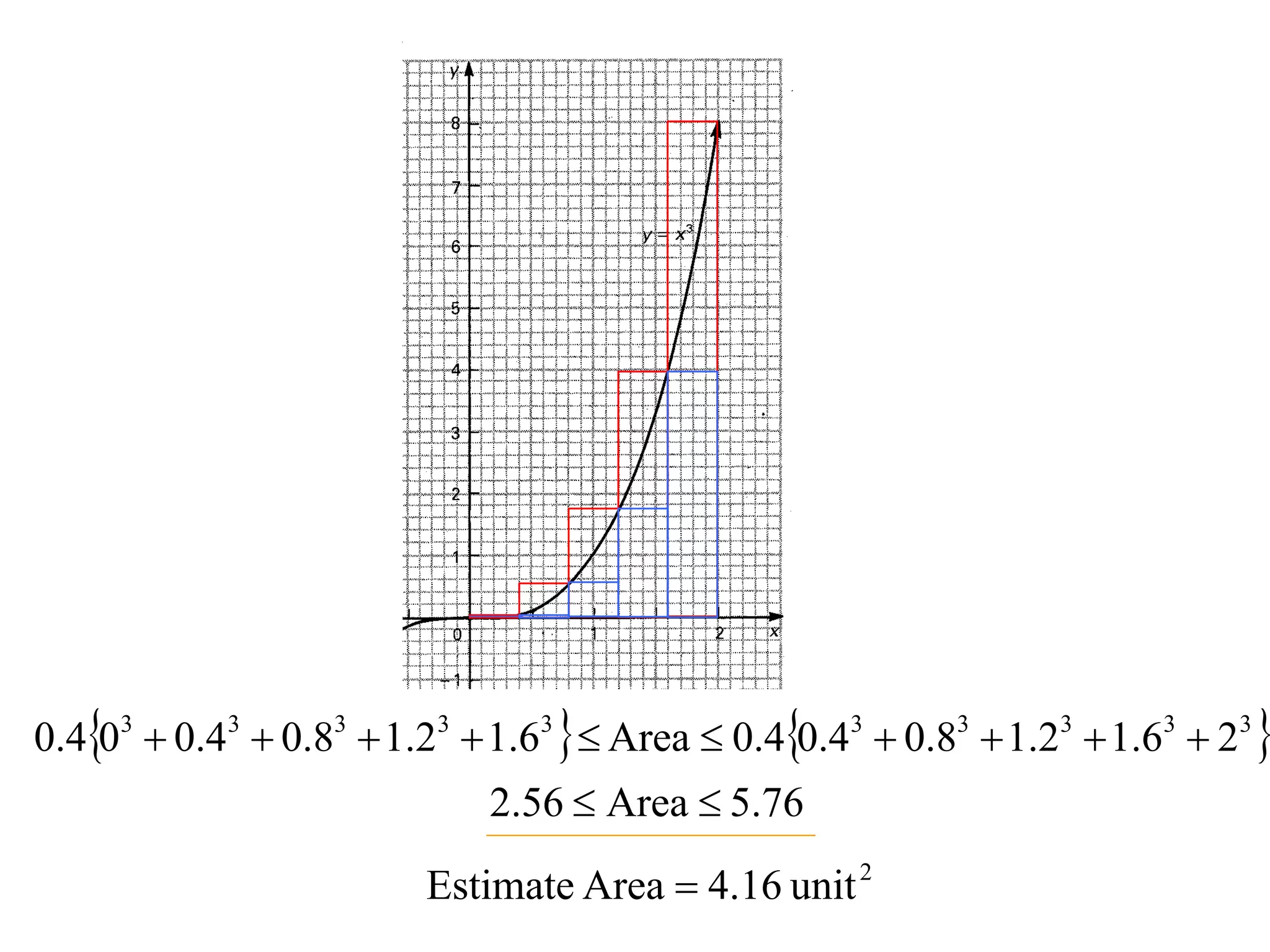
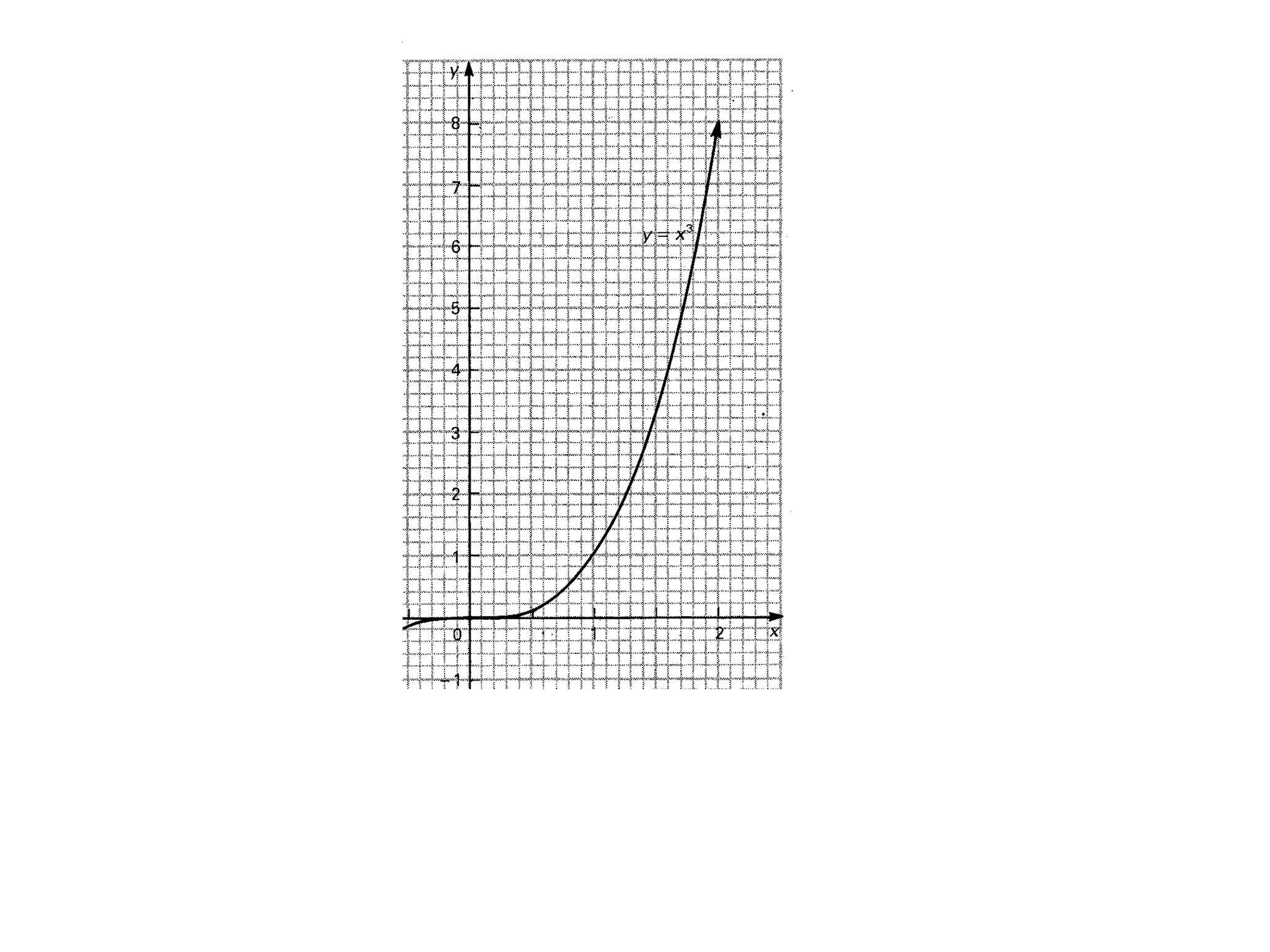
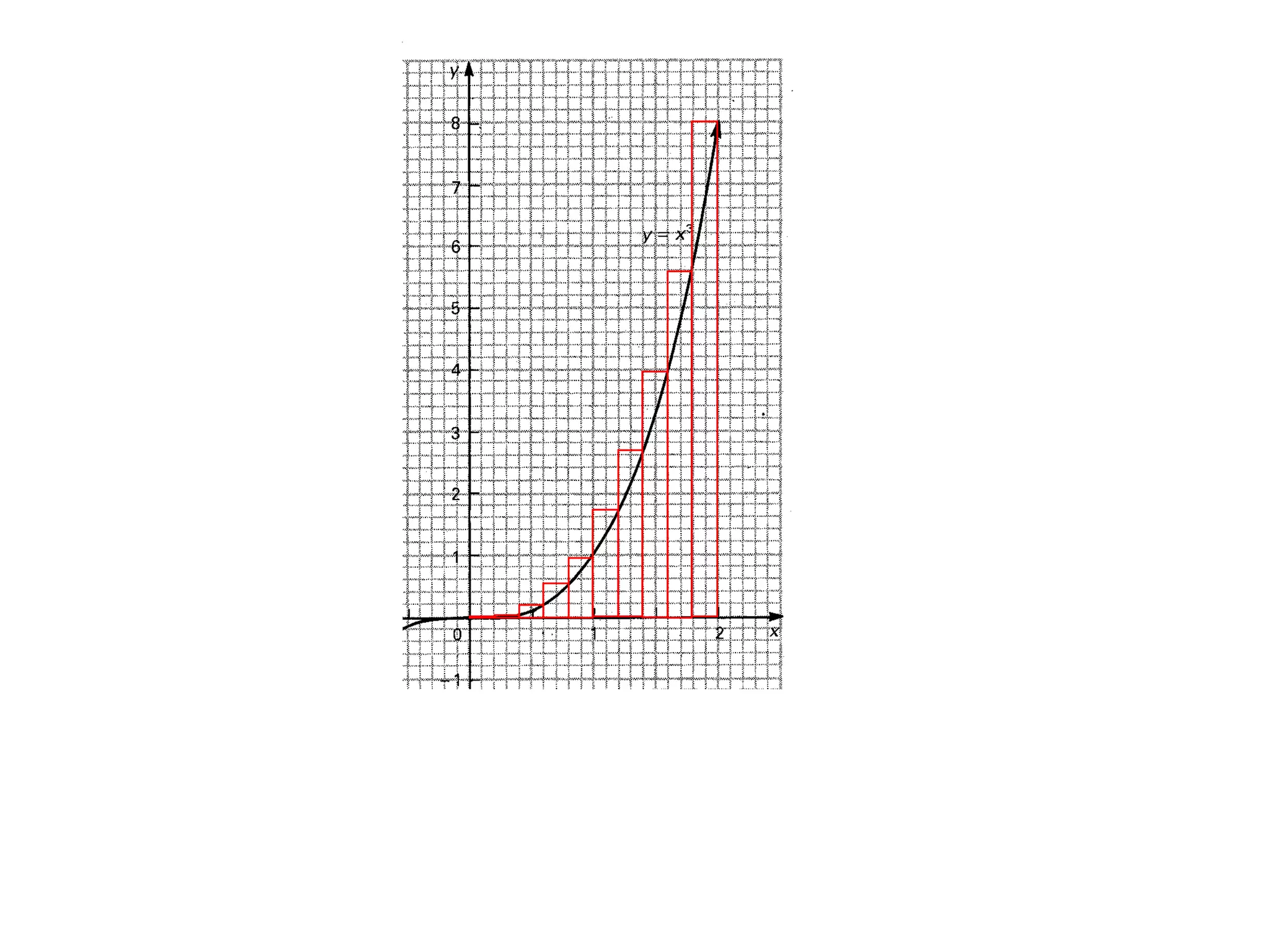
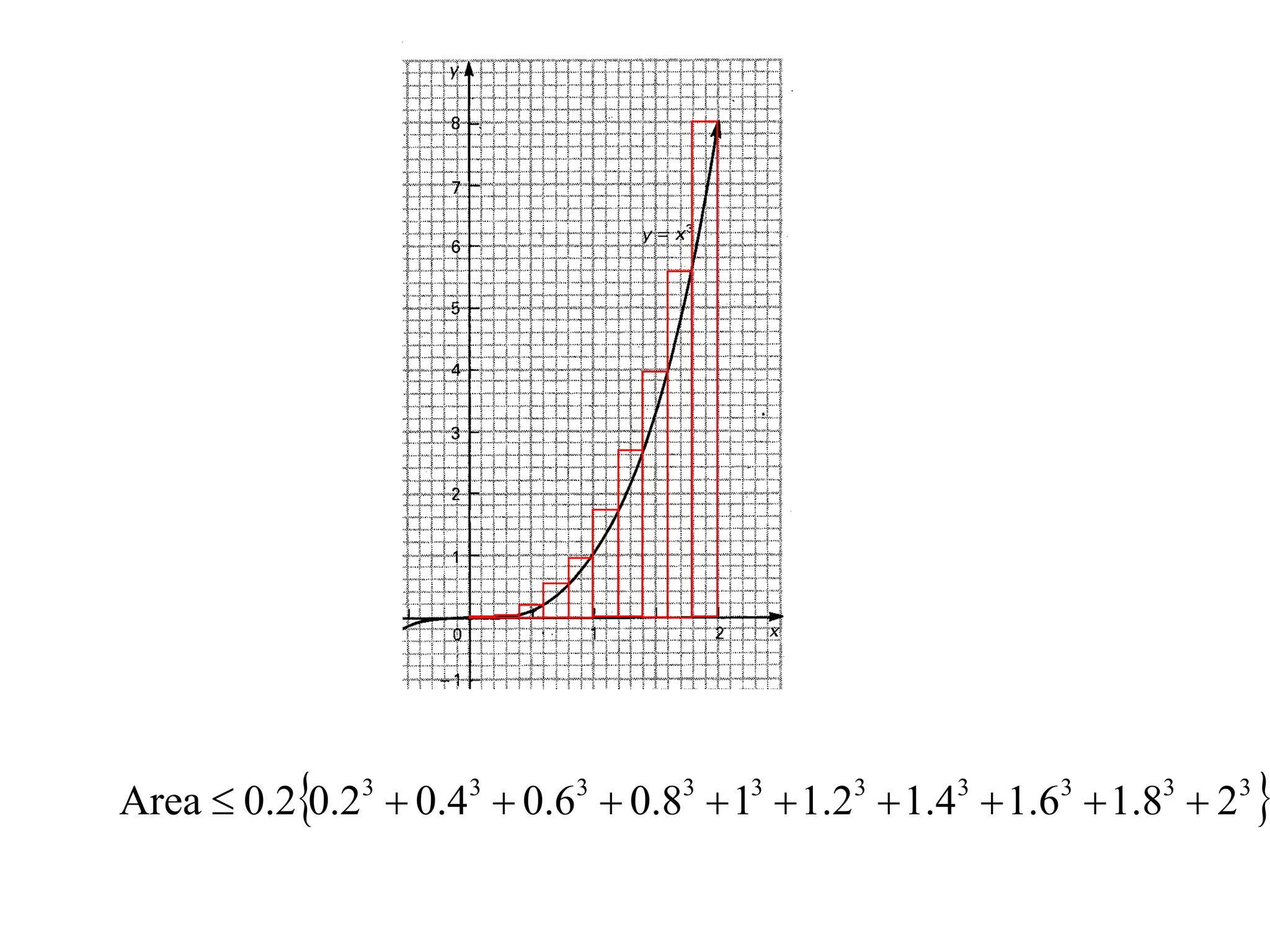
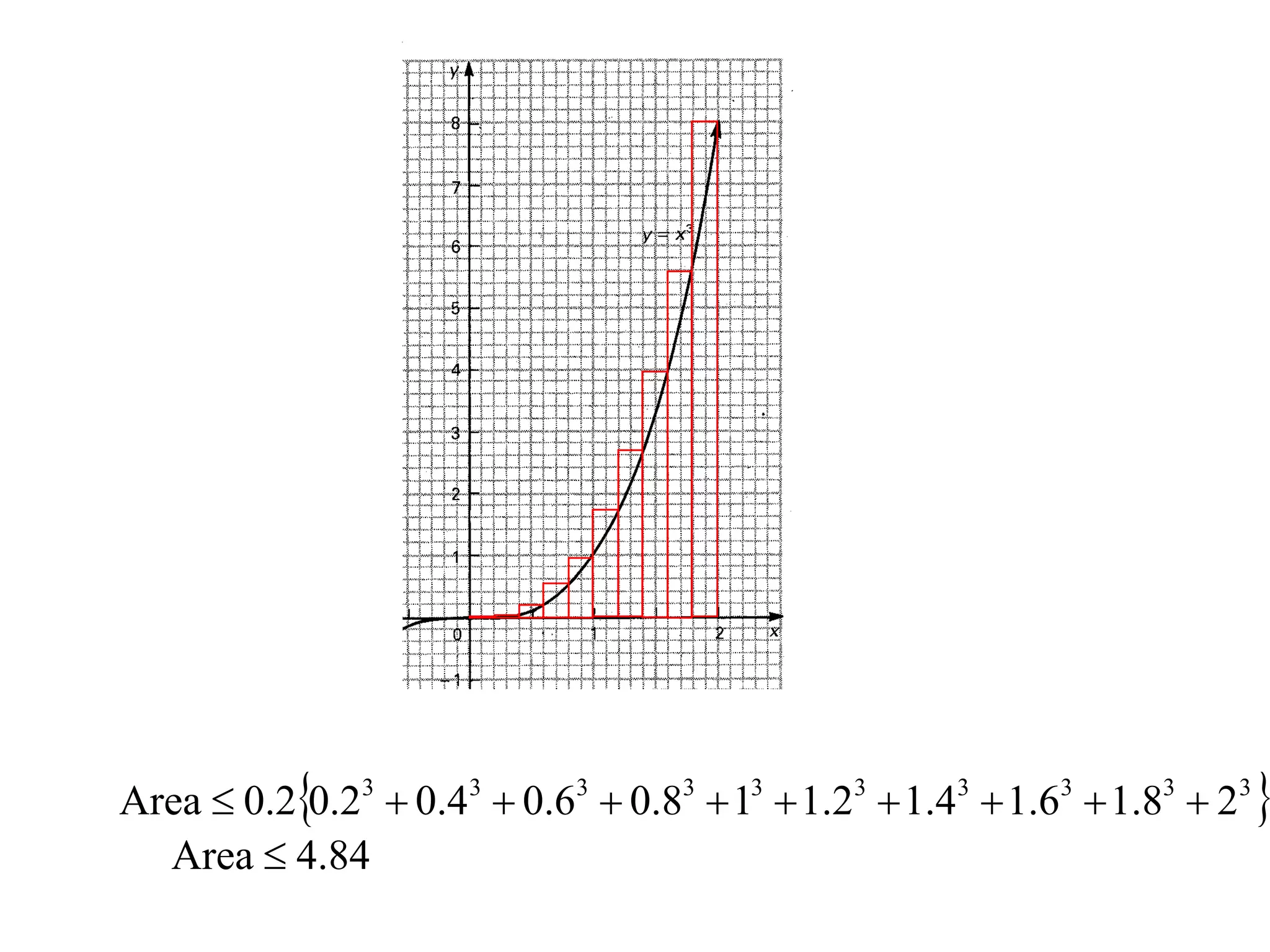
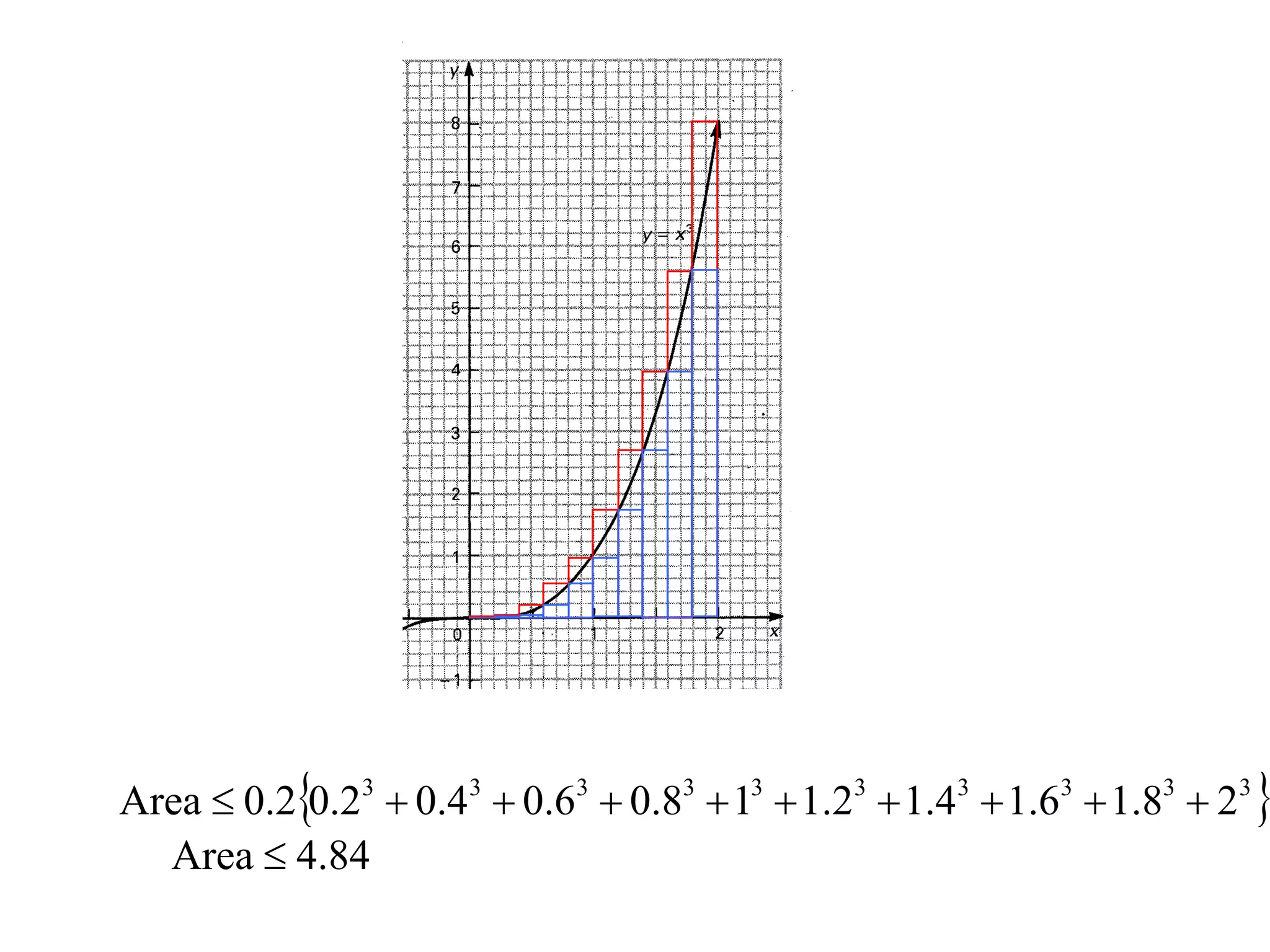
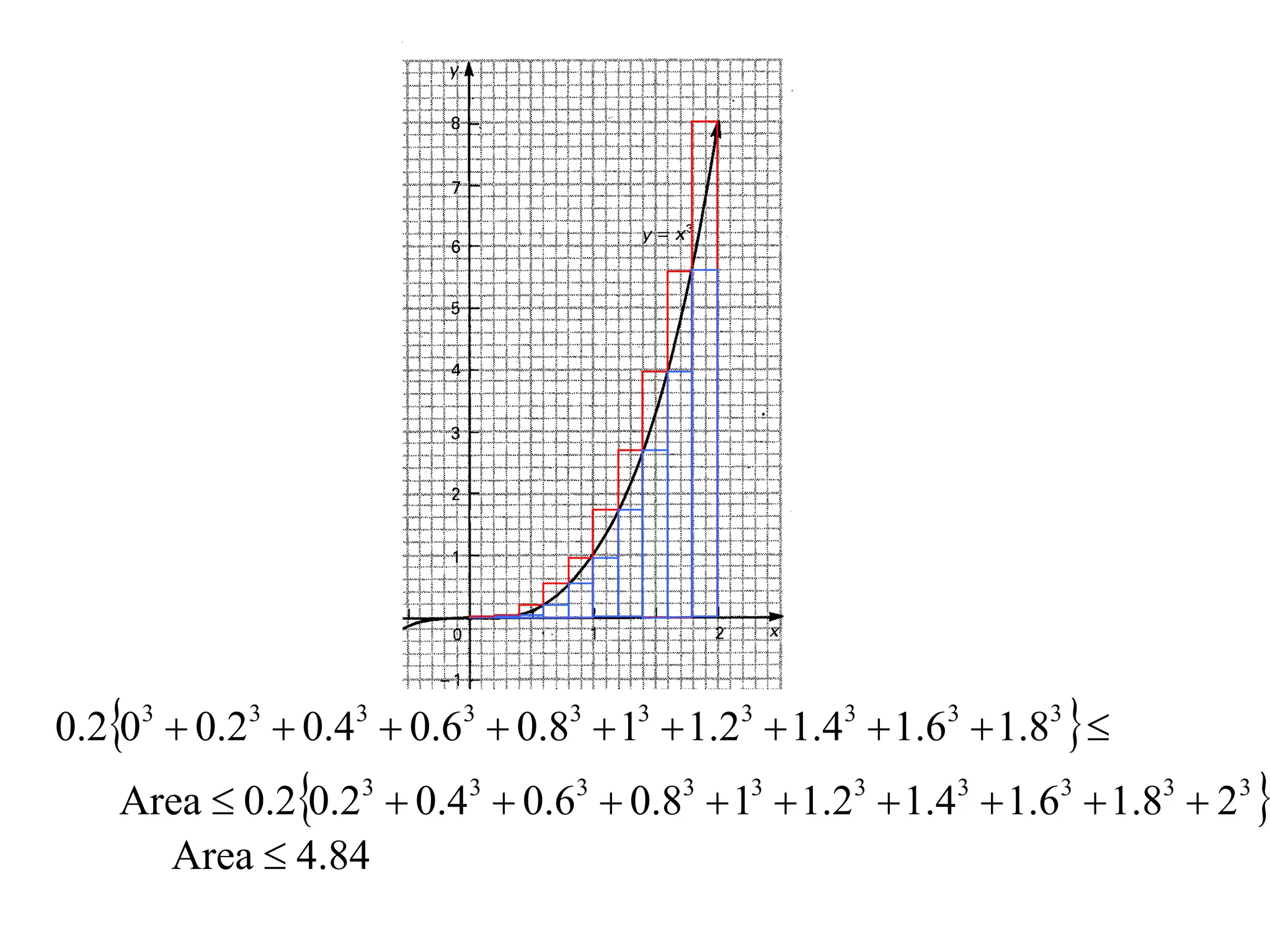
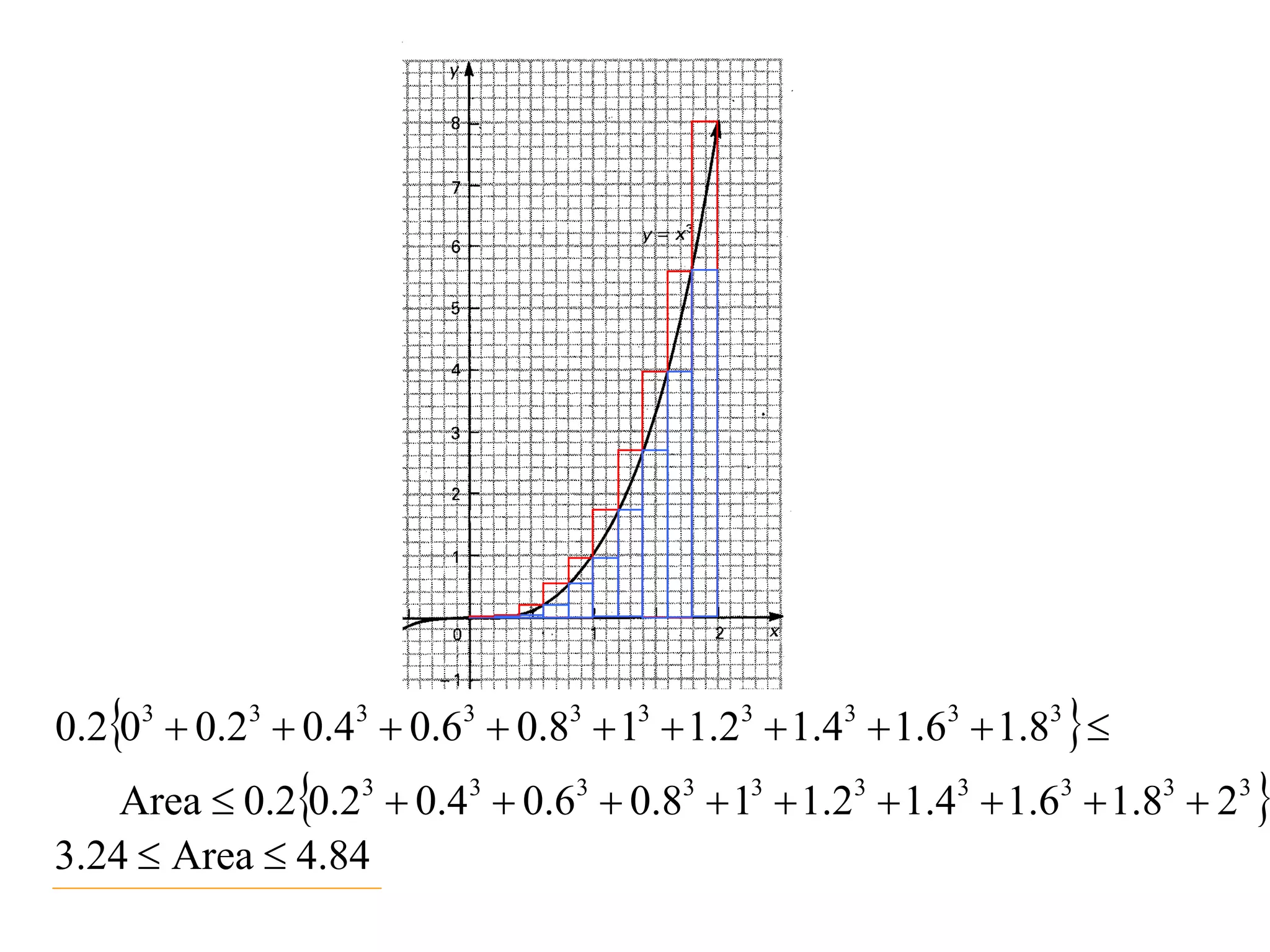
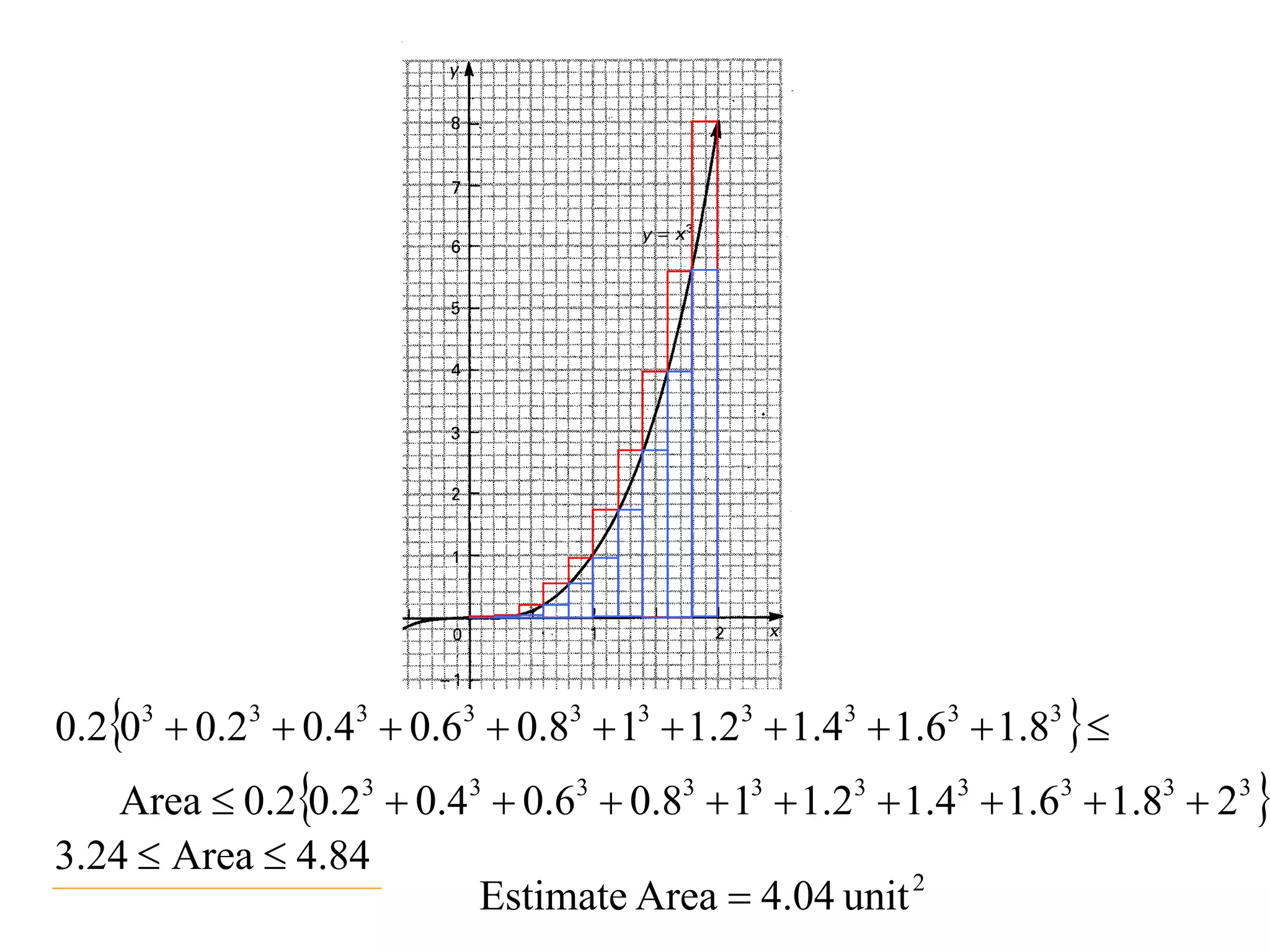
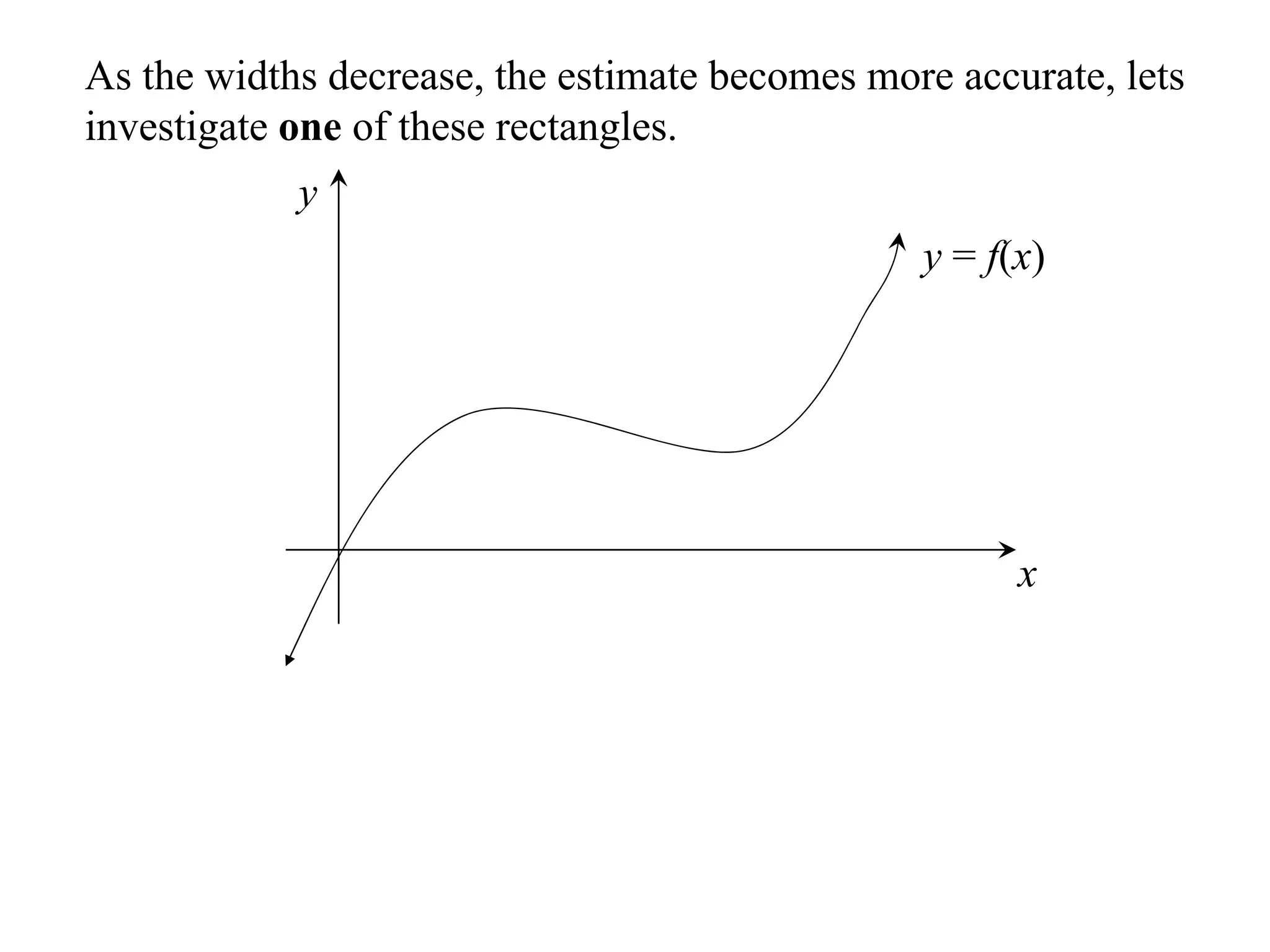
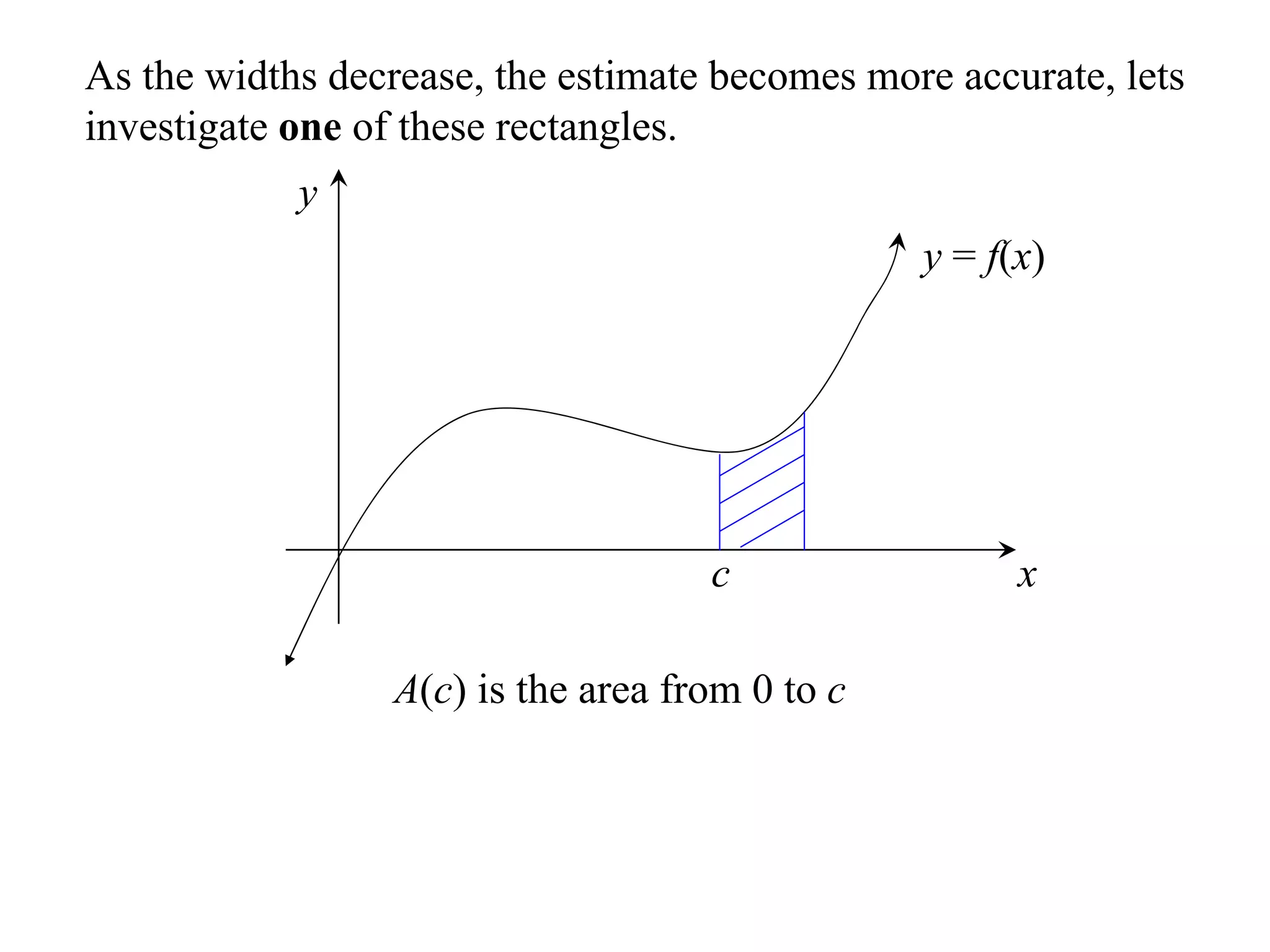
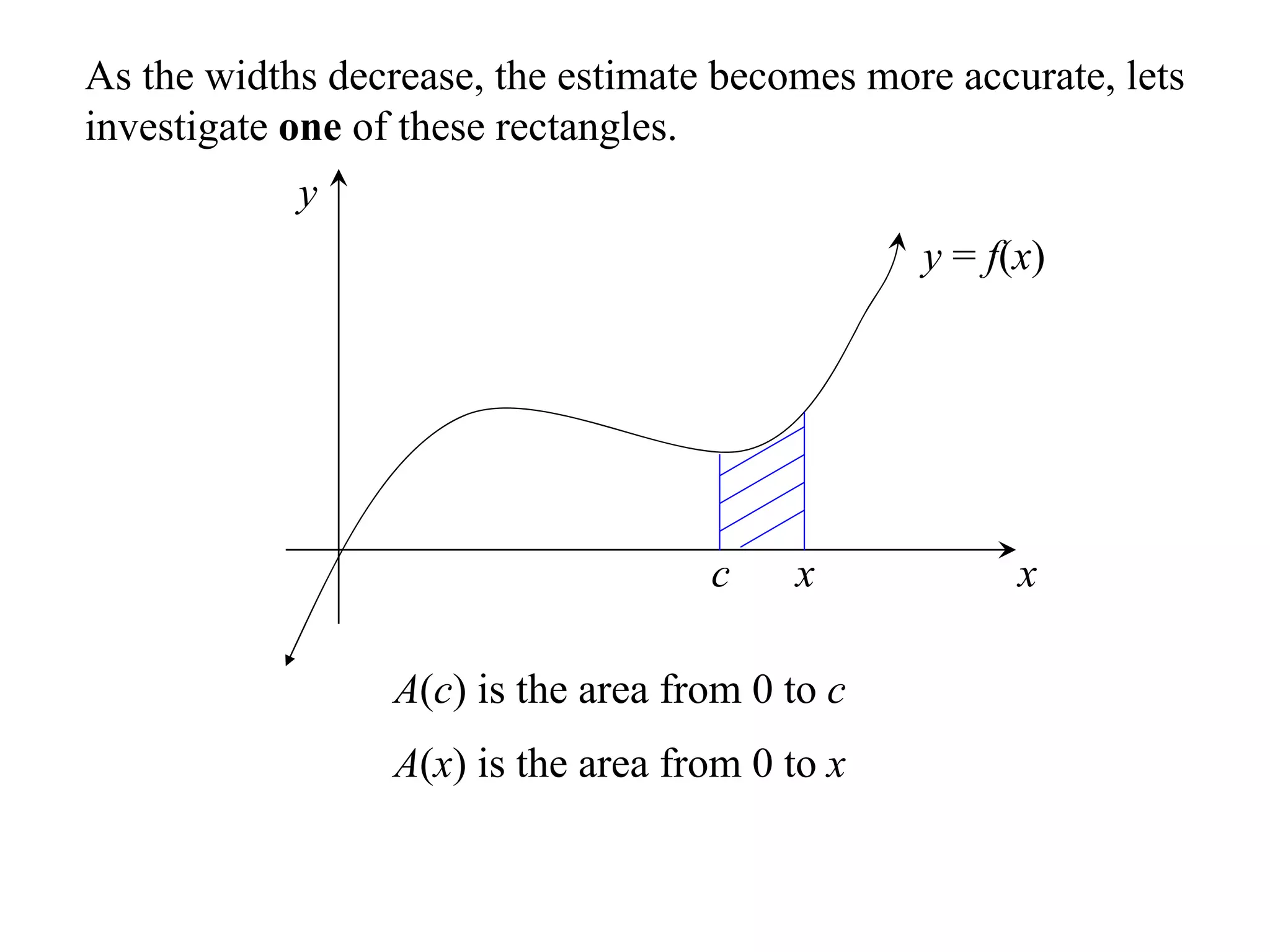
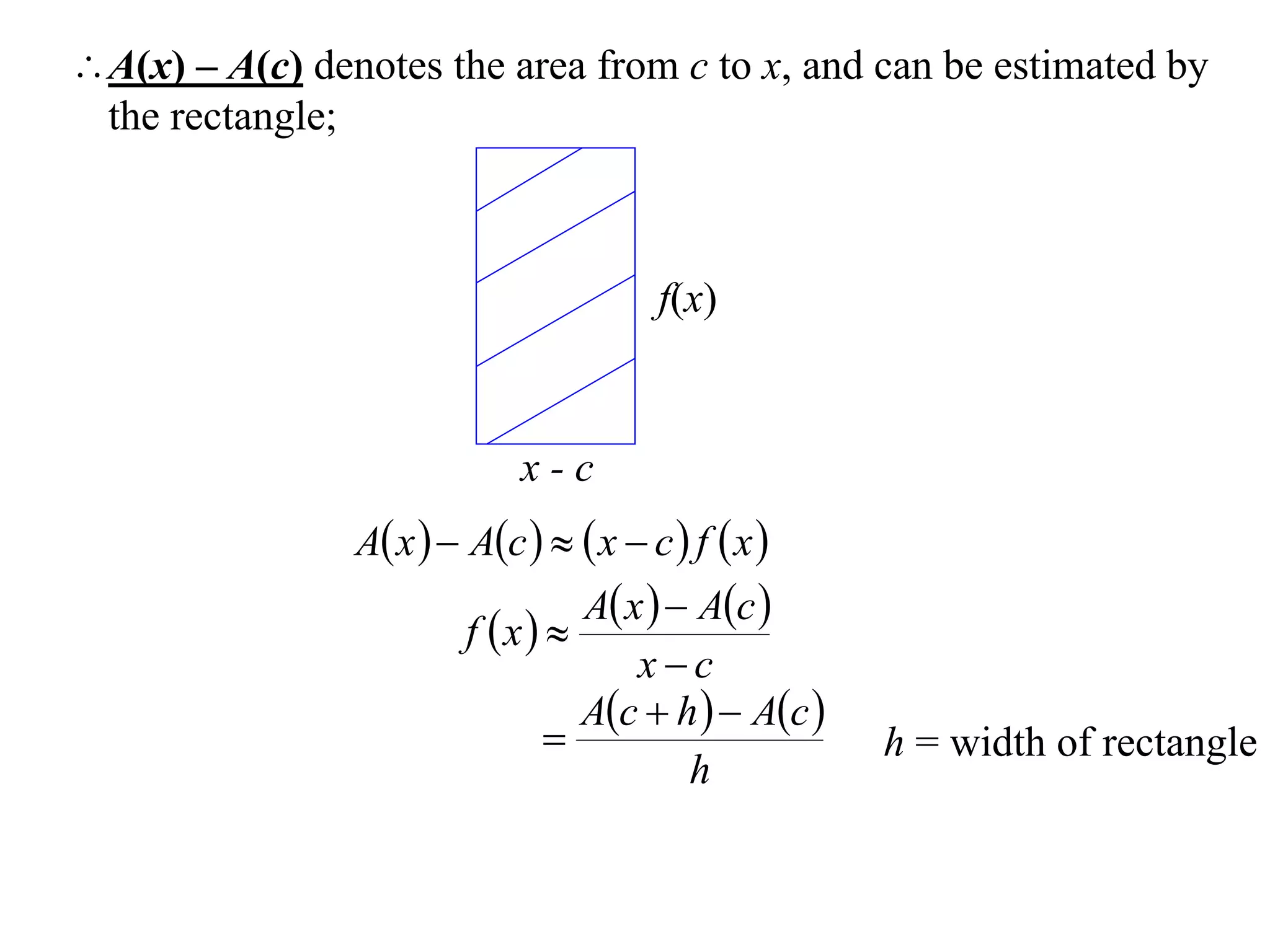
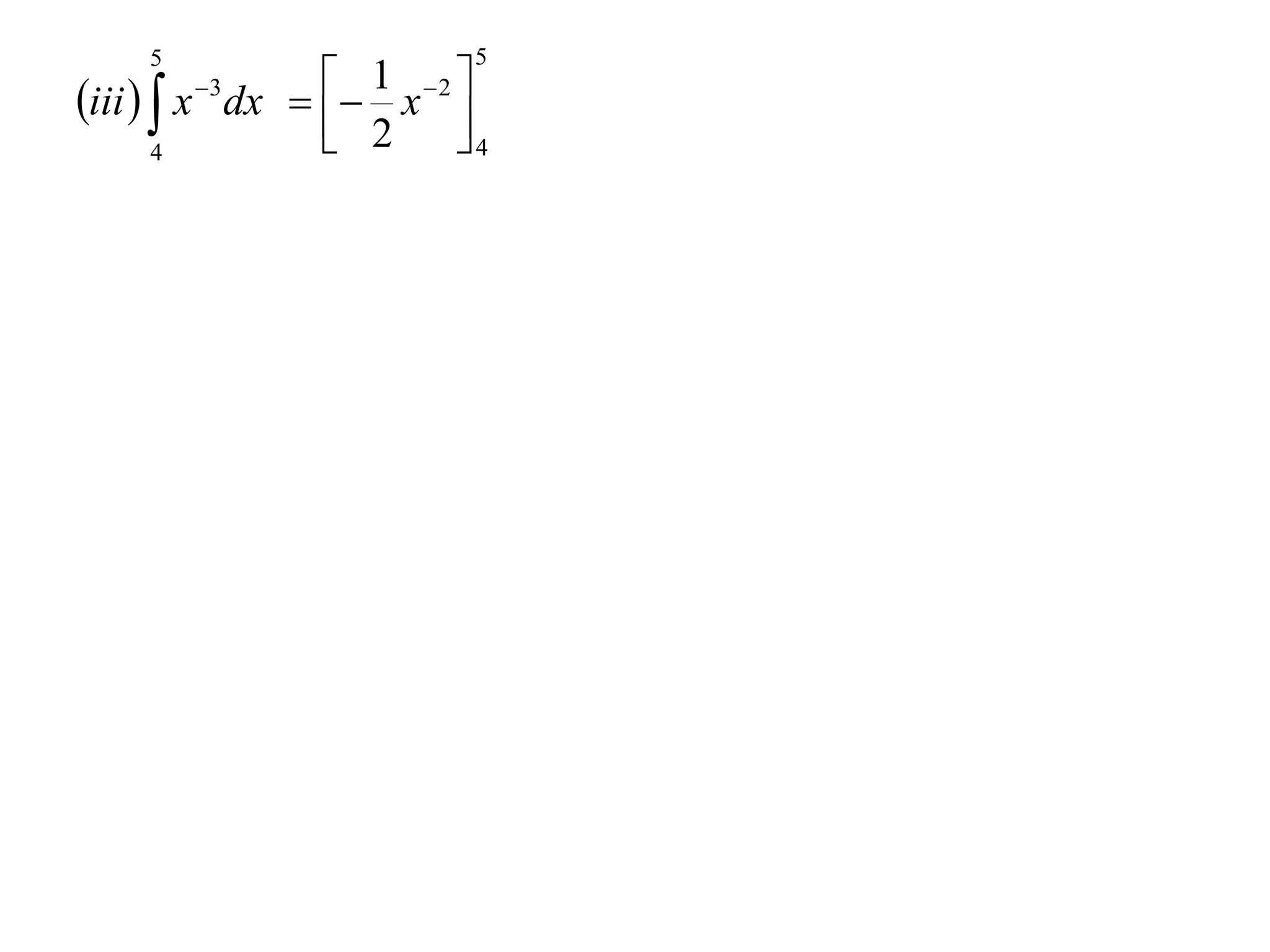The document discusses the concept of integration as the area under a curve. It shows how the area between two points on a curve can be estimated using rectangles, and how taking the width of each rectangle to zero results in the true area being given by the integral of the curve's equation between the two points. Specifically, the area under a curve y=f(x) from x=a to x=b is given by the integral from a to b of f(x) dx, or F(b) - F(a) where F is the antiderivative of f.

1. Integration
Area Under Curve

2. Integration
Area Under Curve

3. Integration
Area Under Curve

4. Integration
Area Under Curve
Area  11  12 
3 3

5. Integration
Area Under Curve
Area  11  12 
3 3
Area  9

6. Integration
Area Under Curve
Area  11  12 
3 3
Area  9

7. Integration
Area Under Curve
10   11  Area  11  12 
3 3 3 3
Area  9

8. Integration
Area Under Curve
10   11  Area  11  12 
3 3 3 3
1  Area  9

9. Integration
Area Under Curve
10   11  Area  11  12 
3 3 3 3
1  Area  9
Estimate Area  5 unit 2

10. Integration
Area Under Curve
10   11  Area  11  12 
3 3 3 3
1  Area  9
Estimate Area  5 unit 2
Exact Area  4 unit 2

13. Area  0.40.43  0.83  1.23  1.63  23 

14. Area  0.40.43  0.83  1.23  1.63  23 
Area  5.76

15. Area  0.40.43  0.83  1.23  1.63  23 
Area  5.76

16. 0.403  0.43  0.83  1.23  1.63   Area  0.40.43  0.83  1.23  1.63  23 
Area  5.76

17. 0.403  0.43  0.83  1.23  1.63   Area  0.40.43  0.83  1.23  1.63  23 
2.56  Area  5.76

18. 0.403  0.43  0.83  1.23  1.63   Area  0.40.43  0.83  1.23  1.63  23 
2.56  Area  5.76
Estimate Area  4.16 unit 2

21. Area  0.20.23  0.43  0.63  0.83  13  1.23  1.43  1.63  1.83  23 

22. Area  0.20.23  0.43  0.63  0.83  13  1.23  1.43  1.63  1.83  23 
Area  4.84

23. Area  0.20.23  0.43  0.63  0.83  13  1.23  1.43  1.63  1.83  23 
Area  4.84

24. 0.203  0.23  0.43  0.63  0.83  13  1.23  1.43  1.63  1.83  
Area  0.20.23  0.43  0.63  0.83  13  1.23  1.43  1.63  1.83  23 
Area  4.84

25. 0.203  0.23  0.43  0.63  0.83  13  1.23  1.43  1.63  1.83  
Area  0.20.23  0.43  0.63  0.83  13  1.23  1.43  1.63  1.83  23 
3.24  Area  4.84

26. 0.203  0.23  0.43  0.63  0.83  13  1.23  1.43  1.63  1.83  
Area  0.20.23  0.43  0.63  0.83  13  1.23  1.43  1.63  1.83  23 
3.24  Area  4.84
Estimate Area  4.04 unit 2

27. As the widths decrease, the estimate becomes more accurate, lets
investigate one of these rectangles.
y
y = f(x)
x

28. As the widths decrease, the estimate becomes more accurate, lets
investigate one of these rectangles.
y
y = f(x)
x

29. As the widths decrease, the estimate becomes more accurate, lets
investigate one of these rectangles.
y
y = f(x)
c x
A(c) is the area from 0 to c

30. As the widths decrease, the estimate becomes more accurate, lets
investigate one of these rectangles.
y
y = f(x)
c x x
A(c) is the area from 0 to c
A(x) is the area from 0 to x

31. A(x) – A(c) denotes the area from c to x, and can be estimated by
the rectangle;

32. A(x) – A(c) denotes the area from c to x, and can be estimated by
the rectangle;
f(x)
x-c

33. A(x) – A(c) denotes the area from c to x, and can be estimated by
the rectangle;
f(x)
x-c
A x   Ac    x  c  f  x 

34. A(x) – A(c) denotes the area from c to x, and can be estimated by
the rectangle;
f(x)
x-c
A x   Ac    x  c  f  x 
A x   Ac 
f x 
xc

35. A(x) – A(c) denotes the area from c to x, and can be estimated by
the rectangle;
f(x)
x-c
A x   Ac    x  c  f  x 
A x   Ac 
f x 
xc
Ac  h   Ac 
 h = width of rectangle
h

36. A(x) – A(c) denotes the area from c to x, and can be estimated by
the rectangle;
f(x)
x-c
A x   Ac    x  c  f  x 
A x   Ac 
f x 
xc
Ac  h   Ac 
 h = width of rectangle
h
As the width of the rectangle decreases, the estimate becomes more
accurate.

37. i.e. as h  0, the Area becomes exact

38. i.e. as h  0, the Area becomes exact
Ac  h   Ac 
f  x   lim
h 0 h

39. i.e. as h  0, the Area becomes exact
Ac  h   Ac 
f  x   lim
h 0 h
A x  h   A x 
 lim
h 0
 as h  0, c  x 
h

40. i.e. as h  0, the Area becomes exact
Ac  h   Ac 
f  x   lim
h 0 h
A x  h   A x 
 lim
h 0
 as h  0, c  x 
h
 A x 

41. i.e. as h  0, the Area becomes exact
Ac  h   Ac 
f  x   lim
h 0 h
A x  h   A x 
 lim
h 0
 as h  0, c  x 
h
 A x 
 the equation of the curve is the derivative of the Area function.

42. i.e. as h  0, the Area becomes exact
Ac  h   Ac 
f  x   lim
h 0 h
A x  h   A x 
 lim
h 0
 as h  0, c  x 
h
 A x 
 the equation of the curve is the derivative of the Area function.
The area under the curve y  f  x  between x  a and x  b is;

43. i.e. as h  0, the Area becomes exact
Ac  h   Ac 
f  x   lim
h 0 h
A x  h   A x 
 lim
h 0
 as h  0, c  x 
h
 A x 
 the equation of the curve is the derivative of the Area function.
The area under the curve y  f  x  between x  a and x  b is;
b
A   f  x dx
a

44. i.e. as h  0, the Area becomes exact
Ac  h   Ac 
f  x   lim
h 0 h
A x  h   A x 
 lim
h 0
 as h  0, c  x 
h
 A x 
 the equation of the curve is the derivative of the Area function.
The area under the curve y  f  x  between x  a and x  b is;
b
A   f  x dx
a
 F b   F a 

45. i.e. as h  0, the Area becomes exact
Ac  h   Ac 
f  x   lim
h 0 h
A x  h   A x 
 lim
h 0
 as h  0, c  x 
h
 A x 
 the equation of the curve is the derivative of the Area function.
The area under the curve y  f  x  between x  a and x  b is;
b
A   f  x dx
a
 F b   F a 
where F  x  is the primitive function of f  x 

46. e.g. (i) Find the area under the curve y  x 3 , between x = 0 and
x= 2

47. e.g. (i) Find the area under the curve y  x 3 , between x = 0 and
2
x= 2
A   x 3 dx
0

48. e.g. (i) Find the area under the curve y  x 3 , between x = 0 and
2
x= 2
A   x 3 dx
0
2
  x4 
1
4 0

49. e.g. (i) Find the area under the curve y  x 3 , between x = 0 and
2
x= 2
A   x 3 dx
0
2
  x4 
1
4 0
 2  04 
1 4
4

50. e.g. (i) Find the area under the curve y  x 3 , between x = 0 and
2
x= 2
A   x 3 dx
0
2
  x4 
1
4 0
 2  04 
1 4
4
 4 units 2

51. e.g. (i) Find the area under the curve y  x 3 , between x = 0 and
2
x= 2
A   x 3 dx
0
2
  x4 
1
4 0
 2  04 
1 4
4
 4 units 2
3
ii   x 2  1dx
2

52. e.g. (i) Find the area under the curve y  x 3 , between x = 0 and
2
x= 2
A   x 3 dx
0
2
  x4 
1
4 0
 2  04 
1 4
4
 4 units 2
3 3
ii   x  1dx  
2 1 x 3  x 

2 3 2

53. e.g. (i) Find the area under the curve y  x 3 , between x = 0 and
2
x= 2
A   x 3 dx
0
2
  x4 
1
4 0
 2  04 
1 4
4
 4 units 2
3 3
ii   x  1dx  
2 1 x 3  x 

2 3 2
1 33  3  1 2 3  2
  
 3   3 

54. e.g. (i) Find the area under the curve y  x 3 , between x = 0 and
2
x= 2
A   x 3 dx
0
2
  x4 
1
4 0
 2  04 
1 4
4
 4 units 2
3 3
ii   x  1dx  
2 1 x 3  x 

2 3 2
1 33  3  1 2 3  2
  
 3   3 
22

3

55. 5
iii   x 3dx
4

56. 5 5
 1  2 
iii   x dx   x 
3
4  2 4

57. 5 5
 1  2 
iii   x dx   x 
3
4  2 4
11 1 
   2  2
2 5 4 
9

800

58. 5 5
 1  2 
iii   x dx   x 
3
4  2 4
   2  2
1 1 1
 
2 5 4 
9

800
Exercise 11A; 1
Exercise 11B; 1 aefhi, 2ab (i,ii), 3ace, 4b, 5a, 7*