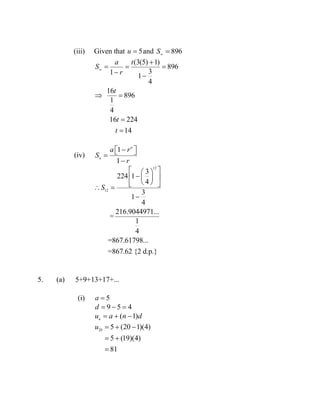
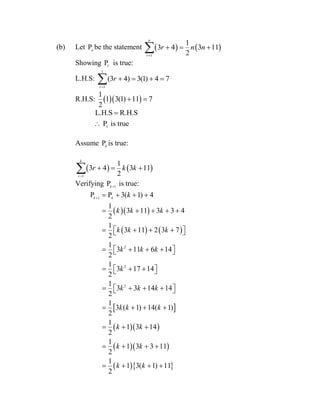This document contains practice questions on sequences, series, and approximations from a CAPE Pure Mathematics unit. Question 1 covers finding terms of sequences defined recursively and evaluating finite sums. Question 2 involves finding expressions for terms of sequences defined recursively and finding their sums. Later questions cover topics like proving identities using induction, evaluating infinite series, approximating functions using Taylor series, and finding roots of equations numerically. The questions provide worked examples of key concepts in sequences, series, and approximations.

1. CAPE Pure Mathematics Unit 2
Practice Questions
By Carlon R. Baird
MODULE 2: SEQUENCES, SERIES AND APPROXIMATIONS
1. (a) Show that  
1
( 1) ( 1)
2
r r r r r    .
(b) Hence show using method of differences that  
1
1
2
n
r
n
r n

  .
(c) Evaluate
20
10
4
r
r

 .
2. (a) Given that
1 1
( 1)! ! ( 1)!
r
r r r
 
 
find
1 ( 1)!
n
r
r
r 
(b)
1
( ) ,
( 1)
f p p
p p
 

ℤ+
(i) Show that ( ) ( 1)
( 1)( 2)
v
f p f p
p p p
  
 
, stating the value of v.
(ii) Hence show that by method of differences, that
2
1
1 (2 3)
( 1)( 2) 4( 1)(2 1)
n
p
n n
S
p p p n n

 
   
(iii) Deduce the sum to infinity of S.
3. (a) Prove by the method of mathematical induction, that, fornℤ+
,
1
2 2 1 ( 1)2
n
r n
r
r n

    
(b) Prove by induction that fornℤ+
, that  
1
1
(3 4) 3 11 .
2
n
r
r n n

  

2. 4. (a) The expressions 2
6, 2 , andx x x form the first three terms of a
geometric progression. By calculating two different expressions for
the common ratio, form and solve an equation in x to find possible
values of the first term.
(b) Dylan invest $D at a rate of interest 4% per annum. After 5 years it
will be worth $10,000. How much (to the nearest penny) will it be
worth after 10 years.
(c) The first three terms of a geometric series are (3 1), (2 2) andt u t u 
(2 1)t u  where t and u are constants.
(i) Use an algebraic method to show that one possible value of u is
5 and to find the other possible value of u.
(ii) For each possible value of u, calculate the value of the common
ratio of the series.
Given that 5u  and that the sum to infinity of the geometric series is
896, calculate:
(iii) The value of t.
(iv) The sum of the first twelve terms of the series giving answer to
2 decimal places.
5. (a) For the arithmetic series 5 9 13 17 ...   
Find:
(i) The 20th
term
(ii) The sum of the first 20 terms.
(b) The sum of the first two terms of an arithmetic series is 47.
The thirtieth term of this series is 62 .
Find:
(i) The first term of the series and the common difference

3. (ii) The sum of the first 60 terms of the series.
6. (a) Find the first four terms of the of the sequence:
1 1
4, 7n n
u u u
  
(b) A sequence of terms { n
U }, 1n  is defined by the recurrence relation
2 1
where is a constantn n n
U U U  
 
Given also that 1 2
2 and 5U U  :
(i) Find an expression in terms of  for 3
U
(ii) Find an expression in terms of  for 4
U
Given that the value of 4
21U  :
(iii) Find the possible values of 
(c) Given that
4 3
4 2
10 1
r
r r
y
r r
 


where 1r  . Show that r
y is
convergent. Hence state the limit it converges to.
7. A sequence 1 2 3 4
, , , ,...u u u u is defined by 1 1
5 3(2 ), 7n
n n
u u u
  
(a) Determine the first four terms of the sequence.
(b) Prove by mathematical induction fornℤ+
, that 5 2n n
n
u   .
8. (a) Use Maclaurin’s theorem to find the first three non-zero terms in the
series expansion of
(1 2 )
ln
1 3
x
x
 
 
  
, and state the interval in x for
which the expansion is valid.
(b) (i) Show using Maclaurin’s theorem that
2
2 33( 3)
sin3 3 3 ...
2
x
e x x x x 


   
where  is a constant.

4. (ii) Given that the first non-zero term in the expansion, in
ascending powers of x, of 3
sin3 ln(1 ) is ,x
e x x x x
   
where  is a constant, find the values of , and   .
9. (a) Show that the Taylor expansion of sin( )x in ascending powers of
6
x
 
 
 
up to the term
2
6
x
 
 
 
is
2
1 3 1
sin( )
2 2 6 4 6
x x x
    
       
   
.
(b) Using the series in (a) find, in terms of , an approximation for
2
sin
9
 
 
 
.
10. Given that 3
cos( ) sin( ) 2 0
dy
x y x y
dx
   and that 1y  at 0x  , use
Taylor’s method to show that, close to 0x  , terms in 4
x and higher powers
can be ignored, 2 311 56
1 2
2 3
y x x x    .
11. (a) Expand fully the expression 3
(1 3 )(1 2 ) .x x 
(b) Expand 3
(2 )y . Hence or otherwise, write down the expansion
2 3
(2 )x x  in ascending powers of x.
(c) The coefficient of 2
x in the expansion of 3
(2 )(3 )x bx  is 45. Find
the possible values of the constant b.
(d) Find the term independent of x in the expansion of
3
2 1
.
2
x
x
 
 
 
12. (a) Use the binomial series to expand  
10
2 3x in ascending powers of x
up to and including the term in 3
x , giving each coefficient as an
integer.
(b) Use your series expansion, with suitable value for x, to obtain an
estimate for 1.9710
, giving your answer to 2 decimal places.

5. 13. (a) Find the binomial expansion of
2
1
x
x
 
 
 
in ascending powers of x as
far as the term in 3
x . State the range of values of x for which the
expansion is valid.
(b) Find an expansion of (1 2 )x up to and including the term in 3
x . By
substituting in 0.01x  , find a suitable decimal approximation to 2
(c) (i) Express
2
6 7 5
(1 )(1 )(2 )
 
  
 
  
as partial fractions.
(ii) Hence or otherwise expand
2
6 7 5
(1 )(1 )(2 )
 
  
 
  
in ascending
powers of as far as the term in 3
 .
(iii) State the set of values of for which the expansion is valid.
14. (a) Evaluate
9!
2!3!4!
.
(b) Prove that
2! 2( 1)! ( 1)!
( 2 )
( )! ! ( 1)!( 1)! ( 1)! !
n n n
n nr n r
n r r r n r n r r
 
    
     
(c) Prove that n n
r n r
C C 

15. (a) ( ) 2 3x
f x x  
(i) Show that there exist a root in the interval [2, 3] using the
intermediate value theorem.
(ii) Using the end points of this interval by interval bisection,
obtain a first and second approximation to x.

6. (b) (i) Using the intermediate value theorem show that one root of the
equation 3
7 2 0x x   lies in the interval [2, 3].
(ii) Use interval bisection to find the root to two decimal places.
16. (a) Show that a root of the equation 2 cos 1 0x x   lies in the interval
[1, 1.5].
(b) Find this root using linear interpolation correct to two decimal places.
17. 3 2
( ) 3 5 4f x x x x   
Taking 1.4 as a first approximation to a root, x, of this equation, use
Newton-Raphson process once to obtain a second approximation to x. Give
your answer to three decimal places.

7. By Carlon R. Baird

8. 1. (a) R.T.S :  
1
( 1) ( 1)
2
r r r r r   
R.H.S:   2 21 1
( 1) ( 1)
2 2
r r r r r r r r        
 
1
2
2
r
r


(b) By method of differences:
 
1 1
1
( 1) ( 1)
2
n n
r r
r r r r r
 
    
(c) Recall that :
1
1 1
( ) ( ) ( )
n n k
r k r r
f r f r f r

  
   
20 20
10 10
4 4
r r
r r
 
  
 
 
1
1 1
1
( 1) ( 1)
2
1
( 1) ( 1)
2
1
1(2) 2(3) 3(4) ... ( 1)( 1 1) ( 1)
2
1(1 1) 2(1) 3(2) 4(3) ... ( 1)
1
2
2
n
r
n n
r r
r r r r
r r r r
n n n n
n n

 
 
    

 
    

         
       


 
6 12 ... ( 1)n n  ( 1)
0 2
n n   
  6 12 ... ( 1)n n  
 
 
1
( 1)
2
1
2
n n
n
n
 
 
 
 

9.    
 
 
20 9
1 1
4
20 9
4 20 1 9 1
2 2
4 10(21) 9(5)
4 210 45
660
r r
r r
 
 
  
 
 
    
 
 
 

 
2. (a) Given that
1 1
( 1)! ! ( 1)!
r
r r r
 
 
(b)
1
( ) ,
( 1)
f p p
p p
 

ℤ+
(i) R.T.S: ( ) ( 1)
( 1)( 2)
v
f p f p
p p p
  
 
L.H.S:
 1 1
1 1
1 1
1 ! ! ( 1)!
1 1
! ( 1)!
1 1 1 1 1 1 1 1 1
1 ... ...
2! 3! 4! ! 2! 3! 4! ( 1 1)! ( 1)!
1
1
2!
n n
r r
n n
r r
r
r r r
r r
n n n
 
 
  
 
 

  
                   
 
 
 
1
3!

1
4!
 ...
1
!n

1
2!
 
 
 
1
3!

1
4!
 ...
1
!n

1
( 1)!
1
1
( 1)!
n
n
  
  
  
 

1 1
( ) ( 1)
( 1) ( 1)( 1 1)
f p f p
p p p p
   
   

10. 1 1
( 1) ( 1)( 2)
( 2)
( 1)( 2)
2
( 1)( 2)
p p p p
p p
p p p
p p p
 
  
 

 

 
2v 
(ii)
2
1
1 (2 3)
R.T.S :
( 1)( 2) 4( 1)(2 1)
n
p
n n
p p p n n


   
2 2
1 1
2 2 2
1 1 1
1 1 2
( 1)( 2) 2 ( 1)( 2)
1 2 1 1 1
2 ( 1)( 2) 2 ( 1) ( 1)( 2)
1 1 1 1 1 1
...
2 1(2) 2(3) 3(4) 4(5) 2 (2 1)
n n
p p
n n n
p p p
p p p p p p
p p p p p p p
n n
 
  
 
   
 
  
     
 
       
 
  
1 1 1 1
...
2(3) 3(4) 4(5) (2 1 1)(2 1 2)
1
+
(2 1)(2 2)
1 1 1
2 2 6
n n
n n

        

  
 
1
12

1
20
 ...
1
2 (2 1)n n


1
6
 
 
  
1
12

1
20
 ...
1
+
2 (2 1)n n




2
1
(2 1)(2 2)
1 1 1
2 2 (2 1)(2 2)
1 (2 1)(2 2) 2
2 2(2 1)(2 2)
1 4 4 2
2
n n
n n
n n
n n
n n n

   
 
  
  
   
  
  
  

2 2
2 2( 1)(2 1)n n
 
 
   

11. 2
2
1 4 6
2 4( 1)(2 1)
1 2(2 3 )
2 4( 1)(2 1)
n n
n n
n n
n n
 
  
  

 
 
2
1
1 (2 3)
( 1)( 2) 4( 1)(2 1)
n
r
n n
S
r r r n n

  
   
(iii)
(2 3)
lim lim
4( 1)(2 1)n n
n n
S
n n 


 
2
2
2
2
2
2 2
2
2 2 2
2
2 3
lim
4 2 2 1
2 3
lim
8 12 4
2 3
lim
8 12 4
3
2
lim
12 4
8
2 0
8 0 0
1
4
n
n
n
n
n n
n n n
n n
n n
n n
n n
n n
n n n
n
n n






    


 


 


 


 


12. 3. (a) Let Pn
be the statement
1
2 2 1 ( 1)2
n
r n
r
r n

    
Showing 1
P is true:
L.H.S.:
1
1
1
2 1(2) 2r
r
r

 
R.H.S.:  1
2 1(1 1)2 2 1 2(0)    
2
1
L.H.S R.H.S
P is true


Assume Pk
is true:
1
2 2 1 ( 1)2
k
r k
r
r k

    
Verifying 1
Pk 
is true
 
 
 
 
 
1
1
1
1
1
1 1
1
1
1
1
1
P P ( 1) 2
2 1 ( 1)2 ( 1) 2
2 2( 1)2 ( 1) 2
2 2 2 ( 1) 2 ( 1)
2 2 ( 1) 2 ( 1)
2 2 ( 1) ( 1)
2 2 2 1 1
2 2 2( 1) 2
2 2 2 ( 1) 1
2 1 ( 1) 1 2
k
k k
k k
k k
k k
k k
k
k
k
k
k
k
k k
k k
k k
k k
k k
k
k
k
k





 





   
       
     
     
    
    
   
   
    
     
1
P is truek 

∴By Principle of Mathematical Induction Pn
holds true n ℤ+

13. (b) Let Pn
be the statement    
1
1
3 4 3 11
2
n
r
r n n

  
Showing 1
P is true:
L.H.S:
1
1
(3 4) 3(1) 4 7
r
r

   
R.H.S:   
1
1 3(1) 11 7
2
 
1
L.H.S R.H.S
P is true


Assume Pk
is true:
   
1
1
3 4 3 11
2
k
r
r k k

  
Verifying 1
Pk 
is true:
  
   
 
  
  
  
1
2
2
2
P P 3( 1) 4
1
3 11 3 3 4
2
1
3 11 2 3 7
2
1
3 11 6 14
2
1
3 17 14
2
1
3 3 14 14
2
1
3 ( 1) 14( 1)
2
1
1 3 14
2
1
1 3 3 11
2
1
1 3( 1) 11
2
k k
k
k k k
k k k
k k k
k
k k k
k k k
k k
k k
k k

   
    
     
     
    
     
   
  
   
   

14. 1
P is truek 

∴By Principle of Mathematical Induction Pn
holds true n ℤ+
4. (a)
From equ’n :
2x
r
a

From equ’n :
2
2 x
r
a

Substituting r into equ’n
2 2
2 2
2
2 2
2
4
4
x x
a a
x x
a a
x ax
 
 
 


From equ’n 6a x 
2 2
2 3 2
3 2
2
4 ( 6)
4 6
10 0
( 10) 0
0 or 10
x x x
x x x
x x
x x
x x
  
 
 
 
  
Possible values of the first term:
0 6 6 6
or
10 6 4 4
a a
a a

      
    
2 2
6
2
a x
ar x
ar x
 



15. (b) $a D
After 1 year:
4
$
100
ar D D
  
    
  
4
$
100
100 4
$
100
104
$
100
D
D
D D
D
 
   
 
   
 
   
$1.04
1.04 1.04
1.04
ar D
D D
r
a D
 
   
After 2 years: 2 2
$(1.04)ar D
Given that after 5 years it will be worth $10,000
5 5
5
(1.04) $10,000
10000
$ $8219.27
(1.04)
ar D
D
  
 
  
 
So Dylan’s initial investment was about $8219.27
Now, after 10 years, i.e 10
ar ,
 
1010
5
10000
1.04
(1.04)
12166.52902
ar
 
   
 

The investment will be worth $12166.53
(c) (3 1)a t u 
2
(2 2)
(2 1)
ar t u
ar t u
 
 
(i)
(2 2) 2 2
(3 1) 3 1
t u u
ar a r
t u u
 
    
 
Rewriting another equation for the third term of the GP:

16. 2
2
2
2
2
(2 2)
(3 1)
(3 1)
(2 2)
(3 1)
(3 1)
(2 2)
3 1
u
ar t u
u
u
t u
u
t u
u
 
    

  




Now we could say that:
2
(2 2)
(2 1)
3 1
t u
t u
u

 

2
2 2
2
2
(2 1)(3 1) (2 2)
6 2 3 1 4 8 4
2 9 5 0
2 10 5 0
2 ( 5) 1( 5) 0
( 5)(2 1) 0
5
or
u u u
u u u u u
u u
u u u
u u u
u u
u
u
    
     
  
   
   
   
 
 
1
2
(ii) When 5u  ;
2(5) 2 12 3
3(5) 1 16 4
r

  

When
1
;
2
u  
1
2 2
1 22
2
31
13 1
22
r
 
       
     
 

17. (iii) Given that 5u  and 896S

(3(5) 1)
896
31 1
4
16
896
1
4
16 224
14
a t
S
r
t
t
t


  
 
 


(iv)
1
1
n
n
a r
S
r
  

12
12
3
224 1
4
3
1
4
216.9044971...
=
1
4
=867.61798...
=867.62 {2 d.p.}
S
  
  
   

5. (a) 5+9+13+17+...
(i) 5a 
9 5 4d   
( 1)n
u a n d  
20
5 (20 1)(4)
5 (19)(4)
81
u   
 


18. (ii)  2 ( 1)
2
n
n
S a n d  
 
 
20
20
2(5) (20 1)(4)
2
10 10 76
=860
S   
 
(b) (i)  2 ( 1)
2
n
n
S a n d  
 2
2
2
2 (2 1)
2
2 47
S a d
S a d
  
  
30
( 1)
29 62
n
u a n d
u a d
  
   
 We have two simultaneous equ’ns:
2 47a d 
29 62a d  
Equ’n  62 12a d   
Substituting a into equ’n 
2( 62 29 ) 47
124 58 47
57 171
3
d d
d d
d
d
   
   
 
 
26a  
(ii)  
 
60
60
2( 26) 59( 3)
2
30 52 177
6870
S    
  
 

19. 6. (a)
The first four terms of the sequence:
7,11,15,19,...
(b) 2 1
,n n n
U U U 
  1 2
2 and 5U U 
(i)
(ii)
(iii) Given that 4
21U 
2
2
2
5 2 5 21
5 2 16 0
5 10 8 16 0
5 ( 2) 8( 2) 0
(5 8)( 2)=0
8
= or = 2
5
 
 
  
  
 
 
   
  
   
   
 
 
(c)
4 3
4 2
10 1
r
r r
y
r r
 


, where 1r 
1
1
2 1 1 1
3 2
4 3
4
7
4 7 4 11
4 11 4 15
4 15 4 19
n n
u u
u
u u u
u u
u u


 

     
    
    
3 1 2 1 1 1
2 1
5 2
U U U U
U U



 
  
 
 
4 3 2
2
(5 2) 5
5 2 5
U U U
 
 
 
  
  

20. 4 3
4 2
4 3
4 4 4
4 2
4 4
4
2
10 1
lim lim
10 1
lim
1 1
10
lim
1
1
10 0 0
1 0
10
rr r
r
r
r r
y
r r
r r
r r r
r r
r r
r r
r
 


  
   
 
  
  
 
 
 
  
  
 
 
 



As lim 10, is convergent
i.e it converges to the limit 10
r rr
y y
 
7. (a)
(b) Let Pn
be the statement 5 2n n
n
u  
Showing 1
P is true:
1
1
1
2 1
2
3 2
3
4 3
5 3(2 )
7
5 3(2 )
5(7) 3(2)
=29
5 3(2 )
5(29) 12
=133
5 3(2 )
5(133) 3(8)
641
n
n n
u u
u
u u
u u
u u

 

 
 
 
 
 
 


21. 1 1
1
1 1
1
5 2 7
P is true
u
u u
  


Assume k
P is true:
5 2k k
k
u  
Verifying k+1
P is true:
1
1
1
1 1
5 3(2 )
=5 5 2 3(2 )
5 5 5 2 3 2
5 2 (5 3)
5 2 (2)
5 2
k
k k
k k k
k k k
k k
k k
k k
u u


 
 
   
     
  
 
 
1
P is truek 

By Principle of Mathematical Induction P holds truen
n  ℤ+
8. (a) Let
(1 2 )
( ) ln
1 3
x
h x
x
 
  
  
1
2
1 1
( ) ln(1 2 ) ln(1 3 )
1 2 3
'( )
2 1 2 1 3
1 3
1 2 1 3
(1 2 ) 3(1 3 )
h x x x
h x
x x
x x
x x 
    
   
        
 
 
   
2 2
2 2
''( ) 1(2)(1 2 ) 3( 3)(1 3 )
2(1 2 ) 9(1 3 )
h x x x
x x
 
 
     
    
3 3
3 3
'''( ) 4(2)(1 2 ) 18( 3)(1 3 )
8(1 2 ) 54(1 3 )
h x x x
x x
 
 
    
   

22. 2 2
3 3
1
(0) ln(1) ln(1) 0
2
1 3
'(0) 1 3 4
1 2(0) 1 3(0)
''(0) 2(1 0) 9(1 0) 2 9 7
'''(0) 8(1 2(0)) 54(1 3(0)) 8(1) 54 62
h
h
h
h
 
 
  
    
 
        
      
By Maclaurin's theorem:
2 3''(0) '''(0)
( ) (0) '(0) ...
2! 3!
h h
h x h h x x x    
2 3
2 3
7 62
( ) 0 4 ...
2! 3!
(1 2 ) 7 31
ln 4 ...
1 3 2 3
h x x x x
x
x x x
x
     
 
     
  
where
1 1
3 3
x  
(b) (i) Let ( ) sinx
f x e x

   
 
'( ) 3cos3 sin3
3cos3 sin3
x x
x
f x e x x e
e x x
 



       
 
   
 
2
2
''( ) 9sin3 3 cos3 3cos3 sin3
9sin3 3 cos3 3 cos3 sin3
9 sin3 6 cos3
x x
x
x
f x e x x x x e
e x x x x
e x x
 


  
  
 
          
      
    
   
   
2 2
2 2 2
2 2 3
2 3
'''( ) 3( 9)cos3 18 sin3 ( 9)sin3 6 cos3
3( 9)cos3 18 sin3 ( 9)sin3 6 cos3
3 27 6 cos3 9 18 sin3
9 27 cos3 27 sin3
x x
x
x
x
f x e x x x x e
e x x x x
e x x
e x x
 



    
    
    
 
                   
       
       
     
(0)
(0) sin(0) 0f e
 

23.  (0)
'(0) 3cos3(0) sin3(0) 3f e
  
 (0) 2
''(0) 9 sin3(0) 6 cos3(0) 6f e
       
   (0) 2 3
2
'''(0) 9 27 cos3(0) 27 sin3(0)
9 27
f e
 

     
 
2 3
By Maclaurin's theorem:
''(0) '''(0)
( ) (0) '(0) ...
2! 3!
f f
f x f f x x x

    
 
 
2
2 3
2 2 3
9 276
( ) 0 3 ...
2! 3!
9
3 3 3 ...
3!
f x x x x
x x x

 

    
    
 2
2 3
3 3
sin3 3 3 ...
2
x
e x x x x



    
(ii) Let ( ) ln(1 )q x x 
1
'( ) (1 )
1
q x x
x

 


  

2
2 2
''( ) ( )(1 )
(1 )
q x x
x
  
 


  
  
2 3
3 3
'''( ) 2( )( )(1 )
2 (1 )
q x x
x
  
 


 
 
1
2 2 2 2
3 3 3 3
(0) ln(1 (0)) ln(1) 0
(0) (1 (0)) (1)
''(0) (1 (0)) (1)
'''(0) 2 (1 (0)) 2 (1) 2
q
q
q
q

   
   
   



   
   
      
   

24. 2 3
2 3
2 3
2 2 3 3
By Maclaurin's theorem:
''(0) '''(0)
( ) (0) '(0) ...
2! 3!
( ) 2
0 ...
2! 3!
1 1
...
2 3
q q
q x q q x x x
x x x
x x x
 

  

    

    
   
2 2 3 31 1
ln(1+ )= ...
2 3
x x x x      
Hence,
In the question we were told that the first non-zero term in the
expansion of 3
sin3 ln(1 ) is ,x
e x x x x
    , this means that the co-
efficient of both x and x2
are 0.
2 0
2


  
 
 
 
2
2 3
2 2 3 3
2 2 2
2
3 3 3
2 3
2 2 3
2 3
2 2 3
3 3
sin3 ln(1 ) 3 3
2
1 1
...
2 3
1
3 3
2
3 3 1
...
2 3
1 3 9
(2 ) 3 ...
2 2 2 3
1 3 9
(2 ) 3 ...
2 2 3 2
x
e x x x x x x
x x x x
x x x x x
x x
x x x
x x x


 
  
  


 
  
 
  

     
    
    

  
  
          
   
  
          
   

25. 2
2
2
1
3 0
2
1
3
2
1 4
3 ( 2) 2
2 2
2
3
 
 


  
 
    

 
2 3
2
3
3 9
2 3 2
2
3
2 93
2 3 2
2 8 9
3 3 2
13
2
 


  
 
     
  
 
9. (a) Let ( ) sinf x x |
1
sin
6 6 2
f
    
    
   
'( ) cosf x x |
3
' cos
6 6 2
f
    
    
   
''( ) sinf x x  |
1
'' sin
6 6 2
f
    
      
   
Using Taylor’s expansion:
   
2''( )
( ) ( ) '( ) ...
2!
f a
f x f a f a x a x a     
2
2
1
1 3 2( ) ...
2 2 6 2! 6
1 3 1
sin( ) ...
2 2 6 4 6
f x x x
x x x
 
 
   
        
   
   
         
   

26. (b)
10. (a) 3
cos( ) sin( ) 2 0
dy
x y x y
dx
  
Differentiating equ’n:
   
 
3
2
2
2
2
2
cos( ) sin( ) 2 0
cos( ) sin( ) cos( ) sin( ) 6 0
cos( ) sin( )
d dy d d
x y x y
dx dx dx dx
d y dy dy dy
x x y x x y
dx dx dx dx
d y dy
x x
dx dx
 
   
 
   
          
 cos( ) sin( )
dy
y x x
dx
  2
2
2
2
6 0
cos( ) cos( ) 6 0
dy
y
dx
d y dy
x y x y
dx dx
 
   
Now, differentiating equ’n 
 
2
2
2
cos( ) cos( ) 6 0
d d y d d dy
x y x y
dx dx dx dx dx
   
    
  
Given the initial conditions 0 0
1 at 0y x 
2
2
2
2 1 3 2 1 2
sin ...
9 2 2 9 6 4 9 6
1 3 1
2 2 18 4 18
1 3 1
2 36 1296
    
 
 
     
          
     
   
     
   
  
 
3 2 2
2
3 2 2
23 2 2
2
3 2 2
cos( ) sin( ) ( sin( )) cos( ) 6 12 0
cos( ) sin( ) sin( ) cos( ) 6 12 0
d y d y dy d y dy dy
x x y x x y y
dx dx dx dx dx dx
d y d y dy d y dy
x x y x x y y
dx dx dx dx dx
      
                  
 
       
 

27. 3
0
0
0
cos(0) (1)sin(0) 2(1) 0
0 2 0
2
dy
dx
dy
dx
dy
dx
 
   
 
 
   
 
 
   
 
Substituting values of 0
x , 0
0
and
dy
y
dx
 
 
 
into equ’n 
   
2
2
2
0
2
2
0
2
2
0
cos(0) (1)cos(0) 6 1 2 0
0 1 0 12 0
11
d y
dx
d y
dx
d y
dx
 
    
 
 
     
 
 
  
 
Substituting values of 0
x ,
2
0 2
0 0
, and
dy d y
y
dx dx
  
   
   
into equ’n 
          
3
2 2
3
0
3
3
0
3
3
0
cos(0) sin(0) 11 (1)sin(0) cos(0) 2 6 1 11 12 1 2 0
0 0 2 66 48 0
112
d y
dx
d y
dx
d y
dx
 
        
 
 
      
 
 
  
 
 To summarize:
2 3
0 0 2 3
0 0 0
0, =1 , = 2 , 11, 112
dy d y d y
x y
dx dx dx
    
        
     
Now using Taylor’s expansion:
     
 
   
2 3
2 3
2 3
0 0
0 0 2 3
0 0 0
''( ) '''( )
( ) ( ) '( ) ...
2! 3!
...
2! 3!
f a f a
f x f a f a x a x a x a
x x x xdy d y d y
y y x x
dx dx dx
       
     
           
     

28. Now substituting values:
    
 
 
 
2 3
2 3
2 3
0 0
1 2 0 11 112 ...
2! 3!
11 56
1 2 ...
2 3
Ignoring other coefficients:
11 56
1 2
2 3
x x
y x
y x x x
y x x x
 
      
    
   
11. (a) Let’s first consider  
3
1 2x
 
3 3 2 3 2 3
1 2
2 3
1 2 1 (1) (2 ) (1)(2 ) (2 )
1 6 12 8
x C x C x x
x x x
    
   
     3 2 3
2 3 2 3 4
4 3 2
1 3 1 2 1 3 1 6 12 8
1 6 12 8 3 18 36 24
24 44 30 9 1
x x x x x x
x x x x x x x
x x x x
      
       
    
(b)                  
3 3 0 2 1 1 2 0 33 3 3 3
0 1 2 32 2 2 2 2y C y C y C y C y    
2 3
3 2
8 12 6
6 12 8
y y y
y y y
   
   
Hence
       
3 3 22 2 2 2
3 3 2 0 3 2 2 1 3 1 2 2 3 0 2 2
0 1 2 3
2 3 4 2
3 2 2 4 6 4 2
3 4 5 6 2 3 4 2
6
2 6 12 8
( ) ( ) ( ) ( ) ( ) ( ) ( ) ( )
+ 6 2 12 12 8
3( ) ( ) 3( )( ) 6 12 12 8
3 3 6 12 6 12 12 8
3
x x x x x x x x
C x x C x x C x x C x x
x x x x x
x x x x x x x x x
x x x x x x x x x
x
        
       
      
        
         
   5 3 2
11 6 12 8x x x x   
(c) First of all, let’s expand  
3
3 bx

29.           
3 2 1 2 33 3 3
1 2
2 2 3 3
3 3 3 3
27 27 9
bx C bx C bx bx
bx b x b x
    
   
     3 2 2 3 3
2 2 3 3 2
2 3 2 27 27 9
54 54 18 2 3 27 ...
x bx x bx b x b x
bx b x b x x bx
       
      
Now considering the coefficients of 2
x
  
2
2
2
2
18 27 45
18 27 45 0
out by 3
6 9 15 0
6 15 6 15 0
3 (2 5) 3(2 5) 0
2 5 3 3 0
5
or 1
2
b b
b b
b b
b b b
b b b
b b
b b
  
  

   
   
   
  
   
(d)
3
The term independent of is
4
x
12. (a)
                 
10 10 0 9 1 8 2 7 310 10 10 10
0 1 2 32 3 2 3 2 3 2 3 2 3 ...x C x C x C x C x         
2 3
1024 15360 10368 414770 ...x x x    
(b) We first must find the value of xobtaining an estimate for  
10
1.97
2 3 1.97
3 2 1.97
0.01
x
x
x
  
 

       
   
3 0 1 2 3
3 2 1 02 3 2 3 2 3 2 3 2
0 1 2 3
6 4 4
2 3
6 3
3
1 1 1 1 1
2 2 2 2 2
1 1 1
3 3
2 4 8
3 3 1
2 4 8
x C x C x C x C x
x x x x x
x x x
x x x
x x
x
         
                 
         
   
       
   
   

30. Now we can substitute x into our series expansion:
 
 
10 2 3
1.97 1024 15360(0.01) 103680(0.01) 414770(0.01) ...
1024 153.6 10.368 0.41477
880.35323
880.35 2 d.p.
    
   


13. (a)    
1 1
2 2
2 2
2 1
1 1
x x
x x
x x
  
    
  
Using the binomial expansion:
  2( 1) ( 1)( 2)
1 1 ...
2! 3!
n n n n n n
x nx x
  
     
1
2
1
2 2 1
2
1
2 1
2
x x
x
 
   
 
 
  
 
1
2 3
2
2 3
2 3
1 1 1 1 1
1 1 2
1 1 1 2 2 2 2 2
2 1 2 1 ...
2 2 2 2! 2 3! 2
1 1 1
2 1 ...
4 8 4 16 8
1 1 1
2 1 ...
4 32 128
x x
x x
x x
x
x x x
       
                                      
         
  
    
        
    
 
     
 
where
1
1
2
x 
 
1
2 32
2 3
1 1 1 1 1
1 1 2
1 2 2 2 2 2
1 1 ...
2 2! 3!
1 3 5
1 ...
2 8 16
x x x x
x x x

      
             
               
 
    

31.    
1 1
2 3 2 32 2
1 1 1 1 3 5
2 1 2 1 ... 1 ...
4 32 128 2 8 16
x x x x x x x x
  
            
  
2 3 2 3 2 3 3
2 2 2 3 3 3 3
2 3
1 3 5 1 1 3 1 1 1
2 1 ...
2 8 16 4 8 32 32 64 128
1 1 3 1 1 5 3 1 1
2 1 ...
2 4 8 8 32 16 32 64 128
1 7 25
2 1 ...
4 32 128
x x x x x x x x x
x x x x x x x x x
x x x
 
           
 
 
           
 
 
     
 
Valid if 1 and 1
2
x
x  
1 for both to be validx 
(a)  
1
2
1 2 1 2x x  
 
   
   
2 3
2 3
2 3
1 1 1 1 1
1 2 1 2 2
1 2 2 2 2 2
1 2 ...
2 2! 3!
1 1
1 4 8 ...
8 16
1 1
1 ...
2 2
x x
x
x x x
x x x
      
          
              
 
     
    
This expansionis valid for 2 1
1
x
x
  
 
Now substituting in 0.01x 

32. 49
1 2(0.01) 0.98
50
49 1
49
50 50
1
7
2 25
7
5 2
  
 
 

     
2 37 1 1
1 0.01 0.01 0.01 ...
2 25 2
1 0.01 0.00005 0.0000005 ...
0.9899495
     
    

7 0.989945 5 2
7
2
0.0989945 5
2 1.41421982
 



(b) (i) Let
   
2
6 7 5
( )
1 1 2 1 1 2
A B C
P
 

     
 
   
     
Multiplying both sides by    1 1 2    

33.         
            
   
2
2
2
6+7 5 1 2 1 2 1 1
Let 1
6 7 1 5 1 0 2 2 3 2 0
18 6
B=3
Let 1
6 7 1 5 1 (2)(1) (0)(1) (0)(2)
4=2
2
Let
A B C
A B C
B
A B C
A
A
       



          

     

 
       

   
2
2
6 7 2 5 2 (3)(0) ( 1)(0) ( 1)(3)
12 3
4
A B C
C
C
 
         
 
 
2 3 4
( )
1 1 2
P 
  
   
  
Valid
1
1
2
 
2 
     
   
1 1 1
2 3 2 3 2 3
2 3 2 3 2 3
2 3
2
2 3
2 1 3 1 4 2
1 1
2 2 2 2 3 3 3 3 2 ...
2 4
1 1
2 2 2 2 3 3 3 3 2 ...
2 4
5
3 2 6 ...
4
6 7 5 5
3 2 6 ...
1 1 2 4
  
        
        
  
 
  
  
  
     
 
             
 
            
    
 
     
  

34. (ii) ss
(iii) All expansions valid for |x|<1
     
    
  
 
   
 
    
  
1 1 1
1 2 3
2 3
2 3
1
( ) 2 1 3 1 4 2
Using binomial expansion:
1 1 1 1 1 1 1 2
2 1 2 1 1 ...
2! 3!
= 2 1 ...
2 2 2 2 ...
Valid for 1
1 1 1
3 1 3 1 1
2
P    
   
  
  

 
  


     
        
       
 
     
    

  
       
   
 
 
 
2 3
2 3
2 3
1
1
1
1
1 1 1 1 2
...
! 3!
3 1 ...
3 3 3 3 ...
Valid for 1
1
1
4 2 4 2 1
2
1
4 2 1
2
1
2 1
2
 
  
  


 







     
    
 
      
    
 
 
  
    
  
 
  
 
 
  
 
 
      
1
1 2 3
2 3
2 3
1 1 1 1 1 1 1 21 1 1 1
2 1 2 1 1 ...
2 2 2! 2 3! 2
1 1 1
2 1 ...
2 4 8
1 1
2 ....
2 4
   
  
  

               
              
         
 
      
    

35. 14. (a)
(b)  2! 2( 1)! ( 1)!
R.T.P : 2
( )! ! ( 1)!( 1)! ( 1)! !
n n n
n nr n r
n r r r n r n r r
 
    
     
N.B.
! ( 1)!
( 1)! ( 1)( )!
( 1)!
( )!
( 1)
! ( 1)!
r r r
n r n r n r
n r
n r
n r
n n n
 
     
 
 
 
 
! 2( 1)!
L.H.S:
( )! ! ( 1)!( 1)!
! 2( 1)!
( 1)! ( 1)!( 1)!( 1)!
( 1)
!( 1) 2( 1)!
( 1)!( 1)! ( 1)!( 1)!
!( 1) 2 ( 1)!
( 1)!( 1)!
( 1)!( 1) 2 ( 1)!
( 1)
n n
n r r r n r
n n
n r r n rr r
n r
n n r n
r n r r r n r
n n r r n
r n r r
n n n r r n
r n r


   

 
     
 
  
 
     
   

  
    

 
  
   
 2
!( 1)!
( 1)! 1 2
1 ! 1 !
( 1)!
2
( 1)! !
r
n n n r r
n r r r
n
n nr n r
n r r

   

  

   
 
9! 9 8 7 6 5 4!
2!3!4!
    

2 1 3 2 1 4!    
15120
12
1260



36. (c) R.T.P: n n
r n rC C 
i.e.
  
! !
!( )! ( )! !
n n
r n r n r n n r

   
  
! !
R.H.S:
( )!( )!( )! !
!
=
!( )!
n n
n r n n rn r n n r
n
r n r

    

15. (a) ( ) 2 3x
f x x  
(i)
(ii)
To summarize: 1st
approximation=2.5
2nd
approximation=2.25
(b) (i) Let 3
( ) 7 2f x x x  
 
3
3
(2) 2 7(2) 2 4 0
(3) 3 7(3) 2 8 0
(2) (3) 0
By the I.V.T such that ( ) 0 in the interval 2,3
f
f
f f
f x
     
    
  
  
 
2
3
(2) 2 2 3 1 0
(3) 2 3 3 8 0
(2) (3) 0
By the Intermediate Value Theorem(I.V.T) such that ( ) 0
in the interval 2,3 .
f
f
f f
f x
     
    
  
  
2 3
(2.5) 0.156854 0
2 2
2.0 2.5
2.0 2.5
(2.25) 0.49317 0
2 2
2.25 2.5
a b
f f f
a b
f f f


    
      
   
 
    
       
   
 

37. (ii)
 
 
2 3
(2.5) 0.125 0
2 2
2< <2.5
2 2.5
2.25 2.359375 0
2
2.25< <2.5
2.25 2.5
(2.375) 1.2285... 0
2
2.375< <2.5
2.4375 0.580
a b
f f f
f f
f f
f



    
      
   

 
    
 

 
    
 

 
 
 
 
32... 0
2.4375< <2.5
2.46875 0.2348... 0
2.46875< <2.5
2.484375 0.05676651... 0
2.484375 < <2.5
2.4921875 0.0336604... 0
2.484375< <2.4921875
2.488
f
f
f
f






  

  

 

 
 
 
28125 0.011666... 0
2.48828125< <2.4921875
2.490234375 0.010968231... 0
2.48828125< <2.490234375
2.49 2 d.p.
f



  

 

 

38. 16. (a) Let ( ) 2 cos( ) 1g x x x 
 
(1) 2(1)cos(1) 1 0.0806046 0
(1.5) 2(1.5)cos(1.5) 1 0.78778... 0
(1) (1.5) 0
By the I.V.T such that ( ) 0 in the interval 1,1.5
g
g
g g
g x
   
    
 
  
(b) ( ) 2 cos( ) 1g x x x 
Using the formula
( ) ( )
( ) ( )
a g b b g a
c
g b g a



Now using linear interplation on the interval
1< <1.5
1| 0.78778| 1.5 0.0806046
1.0464106...
0.78778 0.0806046
(1.0464106) 0.0478365... 0
1.0464106< <1.5
1.04641
Now,
c
g
c


 
 
 
 

 
 
06 0.78778 1.5 0.0478365
1.0723772...
0.78778 0.0478365
(1.0723772) 0.0252732... 0
1.0723772< <1.5
Using linear interpolation on the new interval gives:
1.0723772 0.78778 1.5 0.0252732
0.78
g
c

 

 
 
 


 
1.0856695...
778 0.0252732
(1.0856695) 0.0125400... 0
1.0856695< <1.5
1.0856695 0.78778 1.5 0.0125400
Now, 1.0921615...
0.78778 0.0125400
g
c



 
 
 
 

39.  
(1.0921615) 0.0060289 0
1.0921615< <1.5
1.09 2 d.p.
g
x

 
 
17. 3 2
( ) 3 5 4f x x x x   
First of all, let’s find the derivative of the given function f(x).
 
2
1
'( ) 3 6 5
Using Newton Raphson's process:
'( )
n
n n
n
f x x x
f x
x x
f x

  
 
Given the first approximation 0 1.4x 
 
 
 
1
2 1
2
3 2
2
2
2
( )
'( )
(1.4)
1.4
'(1.4)
(1.4) (1.4) 3(1.4) 5 1.4 4
'(1.4) 3(1.4) 6(1.4) 5
0.136
0.136
1.4 1.45483...
2.48
1.455 3 d.p.
The second approximation 1.
f x
x x
f x
f
f
f
f
x
x
  
 
   
  
 
 
    
 

  455