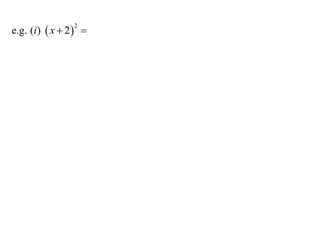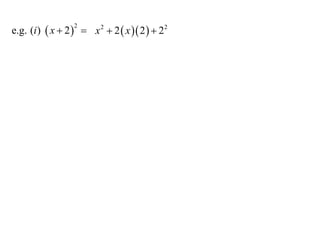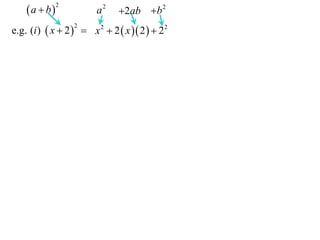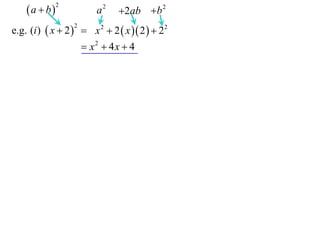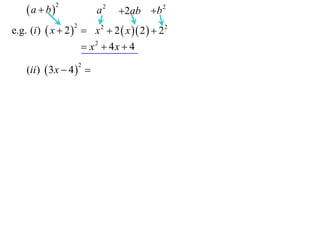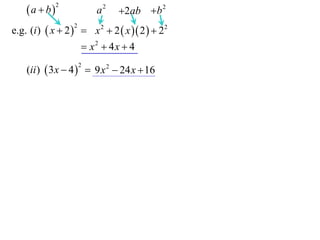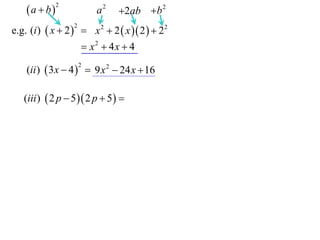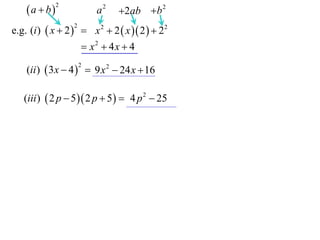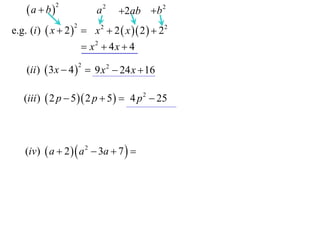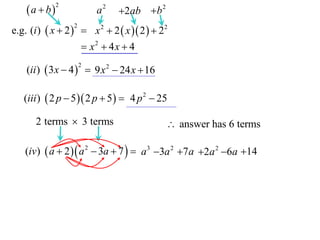Recommended
PDF
X2 t02 04 forming polynomials (2013)
PDF
12X1 T02 01 differentiating exponentials
PDF
12X1 T02 02 integrating exponentials
PDF
X2 t01 02 solving quadratics (2013)
PDF
X2 t01 09 de moivres theorem
PDF
11 X1 T01 02 Binomial Products (2010)
PDF
X2 t01 07 locus & complex nos 1 (2013)
PDF
X2 t01 04 mod arg form(2013)
PDF
Resolução da l ista iii do ii trimestre de 2017
PDF
PDF
X2 t01 08 locus & complex nos 2 (2013)
DOCX
PDF
X2 t01 10 complex & trig (2013)
PDF
Operações com polinômios resolução
PDF
Toan on-thi-dai-hoc-chuyen-de-9-so-phuc
PDF
PPTX
DOCX
บทที่ 1 เรื่องฟังก์ชันเอกซ์โปเนนเชียลและลอการิทึม
PDF
PDF
DOCX
Em 3º ano matemática - (claudia leonardo) - ficha alpha 2
DOC
PPT
PPT
PDF
X2 t02 01 factorising complex expressions (2013)
PPTX
PDF
12 x1 t02 01 differentiating exponentials (2014)
PDF
11 x1 t01 01 algebra & indices (2014)
PDF
12 x1 t02 02 integrating exponentials (2014)
PDF
11 X1 T02 06 relations and functions (2010)
More Related Content
PDF
X2 t02 04 forming polynomials (2013)
PDF
12X1 T02 01 differentiating exponentials
PDF
12X1 T02 02 integrating exponentials
PDF
X2 t01 02 solving quadratics (2013)
PDF
X2 t01 09 de moivres theorem
PDF
11 X1 T01 02 Binomial Products (2010)
PDF
X2 t01 07 locus & complex nos 1 (2013)
PDF
X2 t01 04 mod arg form(2013)
What's hot
PDF
Resolução da l ista iii do ii trimestre de 2017
PDF
PDF
X2 t01 08 locus & complex nos 2 (2013)
DOCX
PDF
X2 t01 10 complex & trig (2013)
PDF
Operações com polinômios resolução
PDF
Toan on-thi-dai-hoc-chuyen-de-9-so-phuc
PDF
PPTX
DOCX
บทที่ 1 เรื่องฟังก์ชันเอกซ์โปเนนเชียลและลอการิทึม
PDF
PDF
DOCX
Em 3º ano matemática - (claudia leonardo) - ficha alpha 2
DOC
Viewers also liked
PPT
PPT
PDF
X2 t02 01 factorising complex expressions (2013)
PPTX
PDF
12 x1 t02 01 differentiating exponentials (2014)
PDF
11 x1 t01 01 algebra & indices (2014)
PDF
12 x1 t02 02 integrating exponentials (2014)
PDF
11 X1 T02 06 relations and functions (2010)
PPT
PPTX
PPT
PPT
Goodbye slideshare UPDATE
PPTX
Math functions, relations, domain & range
PDF
12 x1 t01 02 differentiating logs (2013)
PDF
12 x1 t01 03 integrating derivative on function (2013)
PDF
11 x1 t16 03 indefinite integral (2013)
PDF
X2 t02 02 multiple roots (2013)
PDF
11X1 T14 06 sum of a geometric series (2010)
PDF
Khalilah power point 11 16-10
PPT
More from Nigel Simmons
PPT
PDF
11 x1 t01 03 factorising (2014)
PDF
12 x1 t01 01 log laws (2013)
PDF
X2 t02 03 roots & coefficients (2013)
PDF
11 x1 t16 07 approximations (2013)
PDF
11 x1 t16 06 derivative times function (2013)
PDF
11 x1 t16 05 volumes (2013)
PDF
11 x1 t16 04 areas (2013)
PDF
11 x1 t16 02 definite integral (2013)
PDF
11 x1 t16 01 area under curve (2013)
PDF
X2 t01 11 nth roots of unity (2012)
PDF
X2 t01 06 geometrical representation (2013)
PDF
X2 t01 05 conjugate properties (2013)
PDF
X2 t01 03 argand diagram (2013)
11 x1 t01 02 binomial products (2014) 1. 2. 3. 4. 5. 6. 7. 8. Binomial Products
Bi 2
nomial terms
e.g. x 6 x 1 x 2 x 6 x 6
x2 7 x 6
2
a b a 2 2ab b 2
9. Binomial Products
Bi 2
nomial terms
e.g. x 6 x 1 x 2 x 6 x 6
x2 7 x 6
a b a 2 2ab b 2
2
a b a 2 2ab b 2
2
10. Binomial Products
Bi 2
nomial terms
e.g. x 6 x 1 x 2 x 6 x 6
x2 7 x 6
a b a 2 2ab b 2
2
a b a 2 2ab b 2
2
a b a b a 2 b 2
11. 12. e.g. (i ) x 2 x 2 2 x 2 22
2
13. 14. 15. a b
2
a2
2ab b 2
e.g. (i ) x 2 x 2 2 x 2 22
2
x2 4x 4
(ii ) 3 x 4
2
16. a b
2
a2
2ab b 2
e.g. (i ) x 2 x 2 2 x 2 22
2
x2 4x 4
(ii ) 3 x 4 9 x 2 24 x 16
2
17. a b
2
a2
2ab b 2
e.g. (i ) x 2 x 2 2 x 2 22
2
x2 4x 4
(ii ) 3 x 4 9 x 2 24 x 16
2
(iii ) 2 p 5 2 p 5
18. a b
2
a2
2ab b 2
e.g. (i ) x 2 x 2 2 x 2 22
2
x2 4x 4
(ii ) 3 x 4 9 x 2 24 x 16
2
(iii ) 2 p 5 2 p 5 4 p 2 25
19. a b
2
a2
2ab b 2
e.g. (i ) x 2 x 2 2 x 2 22
2
x2 4x 4
(ii ) 3 x 4 9 x 2 24 x 16
2
(iii ) 2 p 5 2 p 5 4 p 2 25
(iv) a 2 a 2 3a 7
20. a b
2
a2
2ab b 2
e.g. (i ) x 2 x 2 2 x 2 22
2
x2 4x 4
(ii ) 3 x 4 9 x 2 24 x 16
2
(iii ) 2 p 5 2 p 5 4 p 2 25
2 terms 3 terms
(iv) a 2 a 2 3a 7
answer has 6 terms
21. a b
2
a2
2ab b 2
e.g. (i ) x 2 x 2 2 x 2 22
2
x2 4x 4
(ii ) 3 x 4 9 x 2 24 x 16
2
(iii ) 2 p 5 2 p 5 4 p 2 25
2 terms 3 terms
answer has 6 terms
(iv) a 2 a 2 3a 7 a 3 3a 2 7a 2a 2 6a 14
22. a b
2
a2
2ab b 2
e.g. (i ) x 2 x 2 2 x 2 22
2
x2 4x 4
(ii ) 3 x 4 9 x 2 24 x 16
2
(iii ) 2 p 5 2 p 5 4 p 2 25
2 terms 3 terms
answer has 6 terms
(iv) a 2 a 2 3a 7 a 3 3a 2 7a 2a 2 6a 14
a 3 a 2 a 14
23. a b
2
a2
2ab b 2
e.g. (i ) x 2 x 2 2 x 2 22
2
x2 4x 4
(ii ) 3 x 4 9 x 2 24 x 16
2
(iii ) 2 p 5 2 p 5 4 p 2 25
2 terms 3 terms
answer has 6 terms
(iv) a 2 a 2 3a 7 a 3 3a 2 7a 2a 2 6a 14
a 3 a 2 a 14
Exercise 1B; 1ch, 2c, 3be, 5ceg, 7ac, 8b, 9b, 10, 11ace, 13bd, 15*