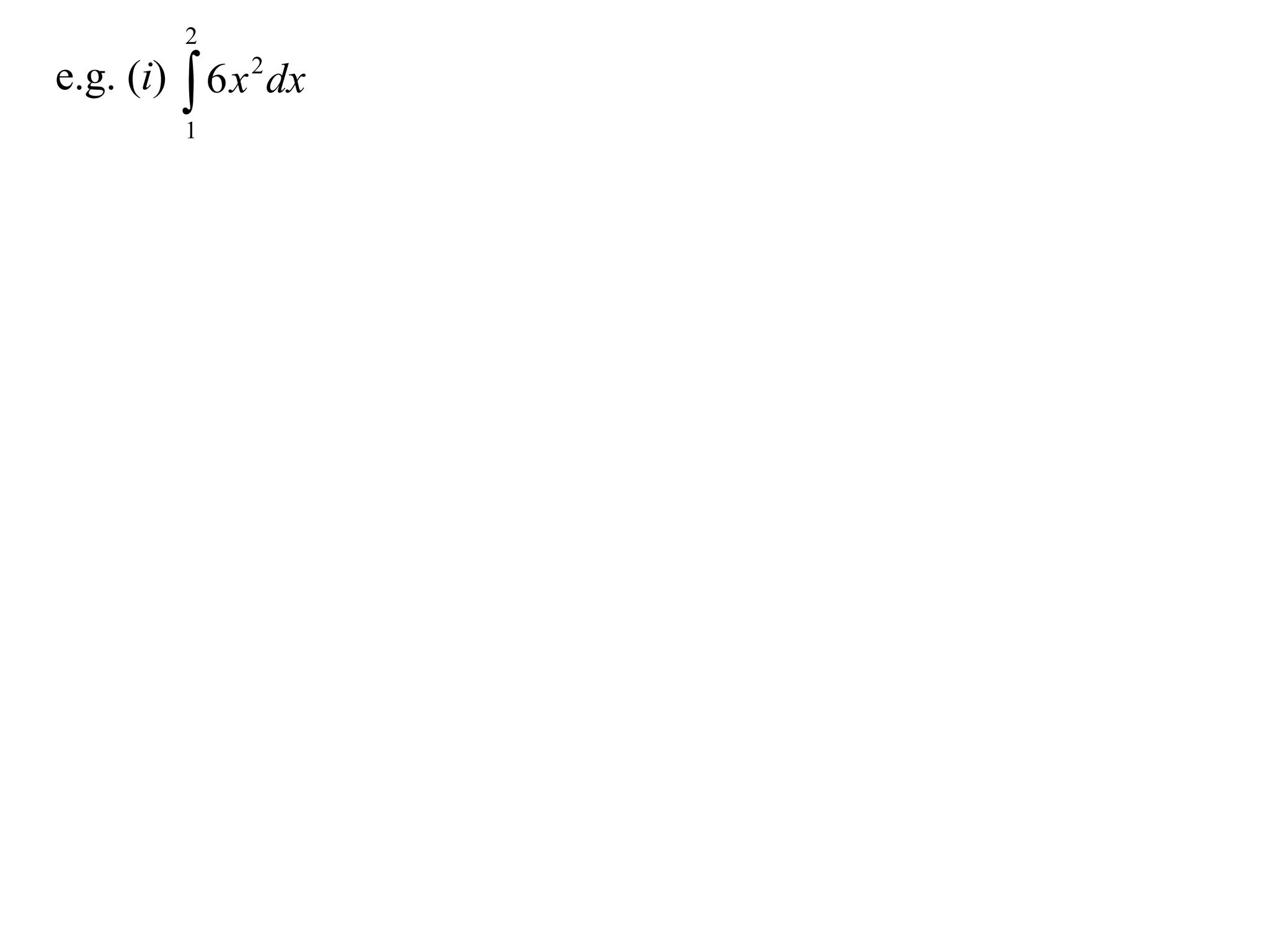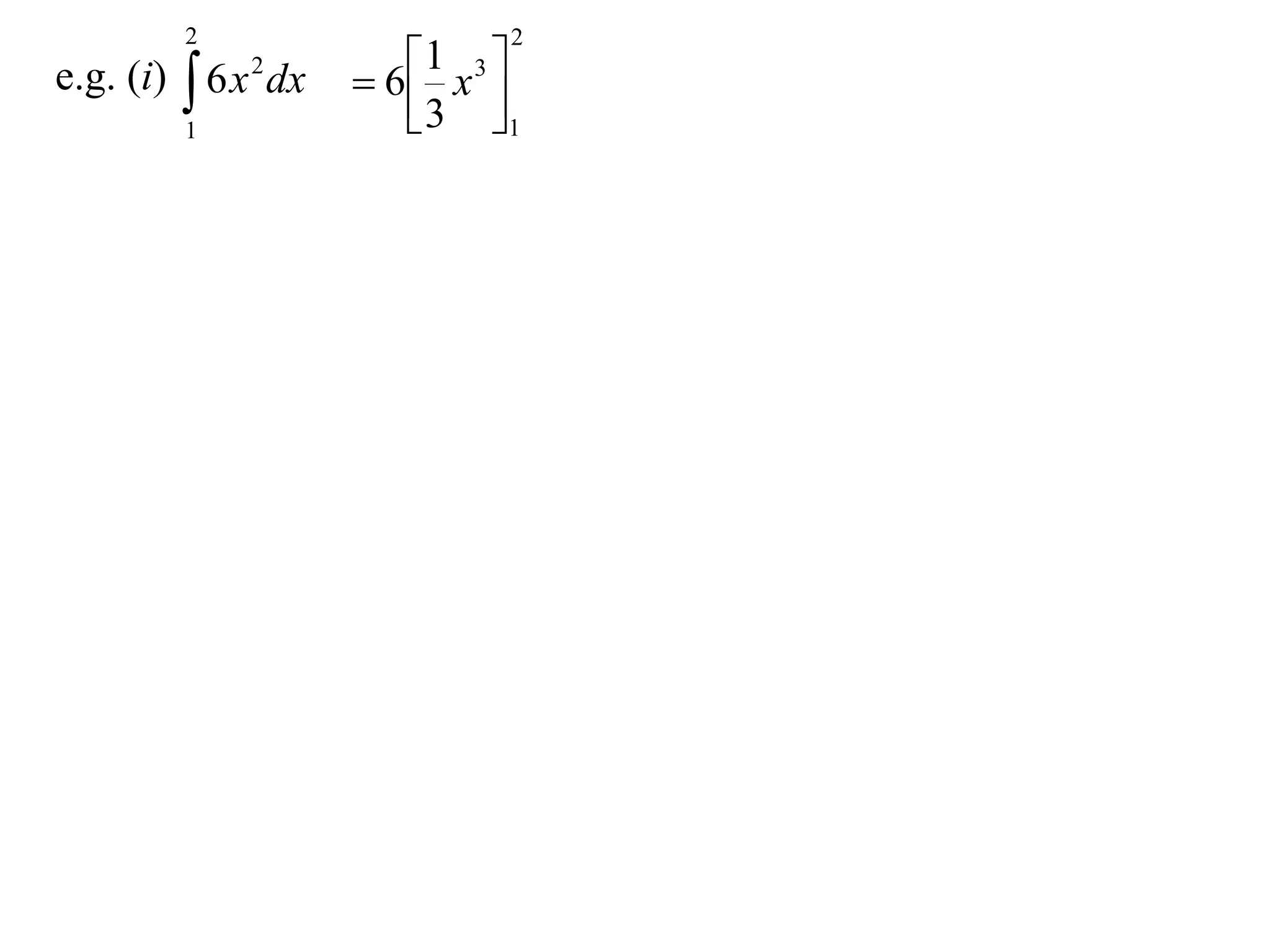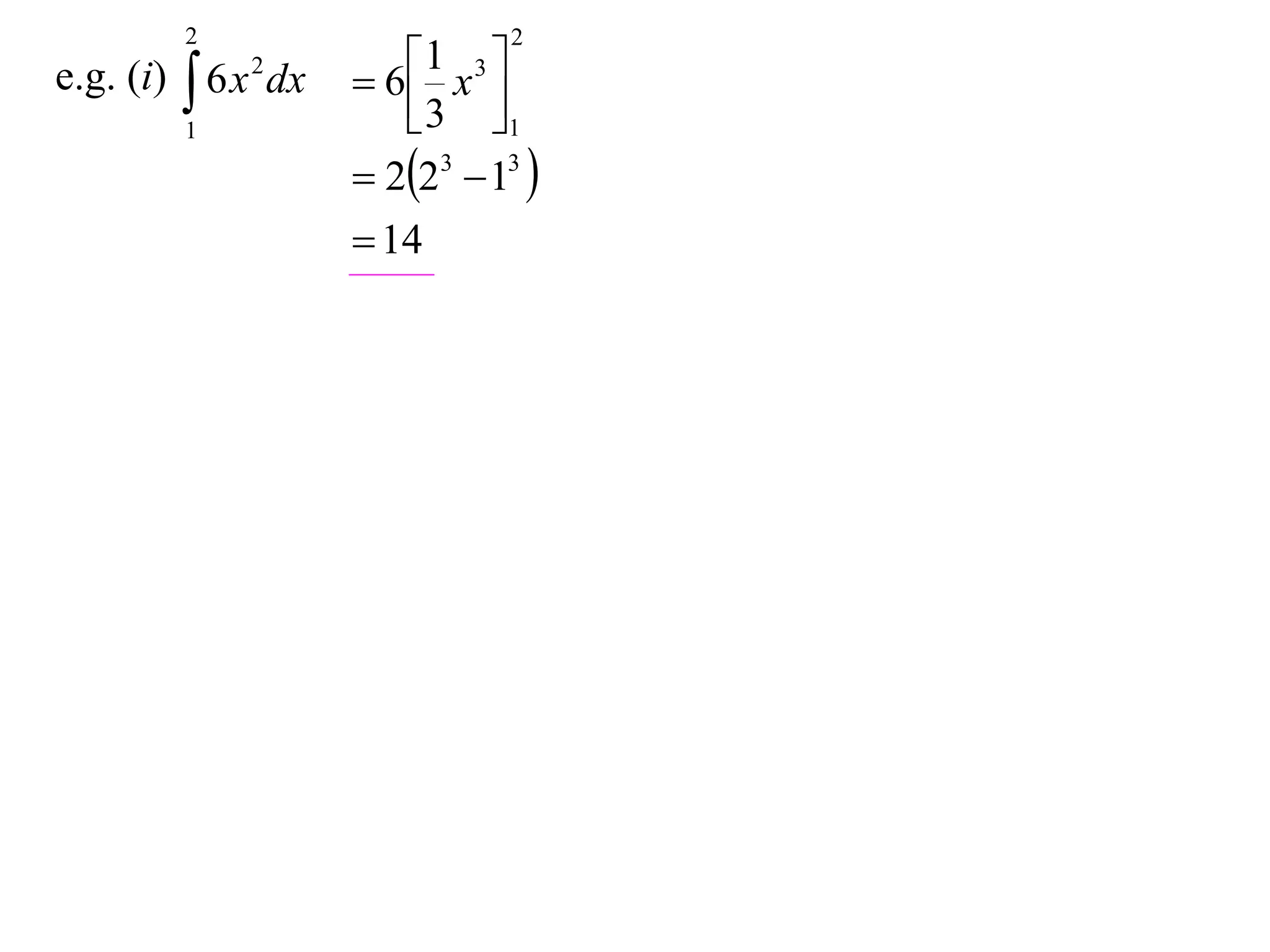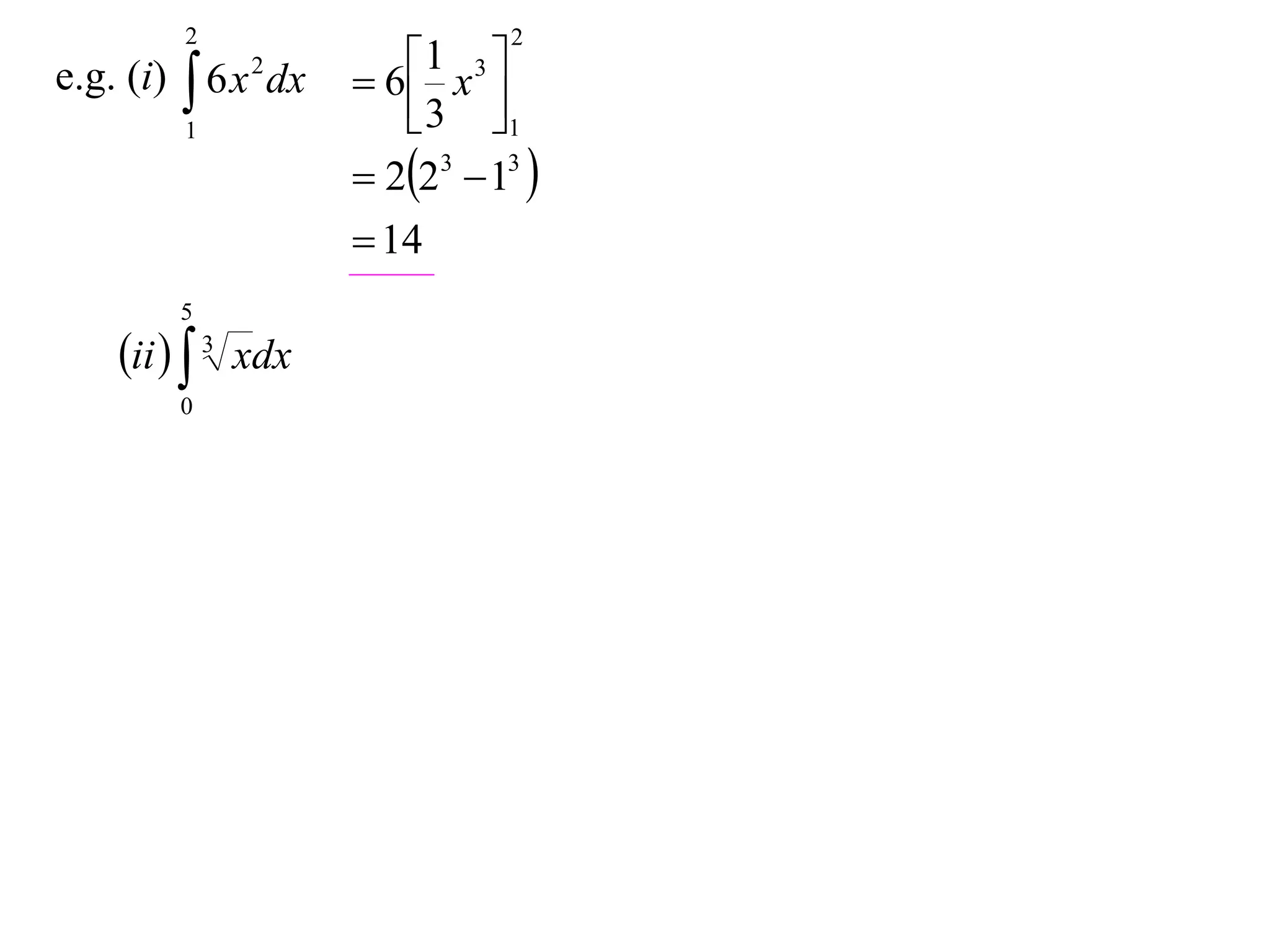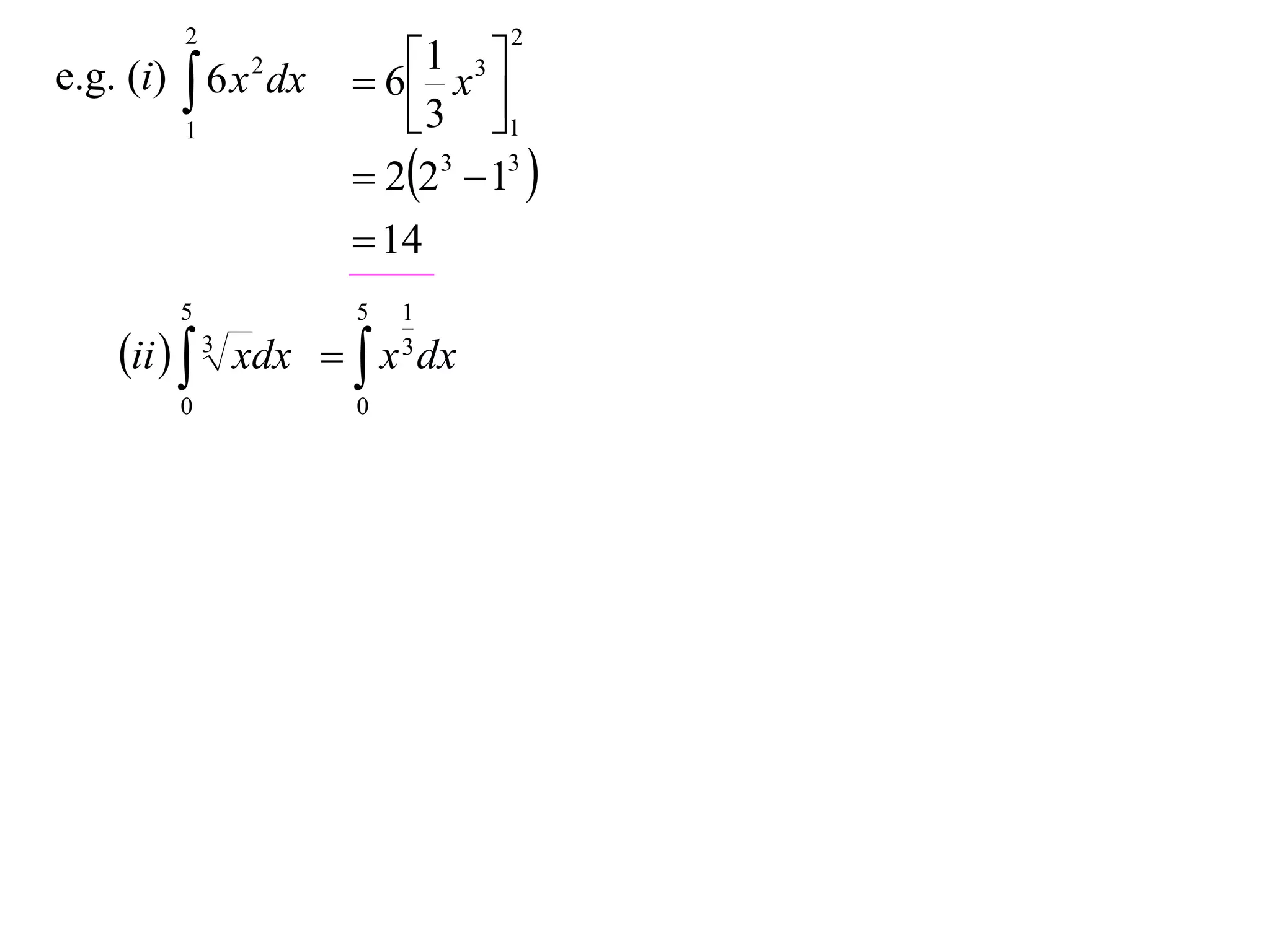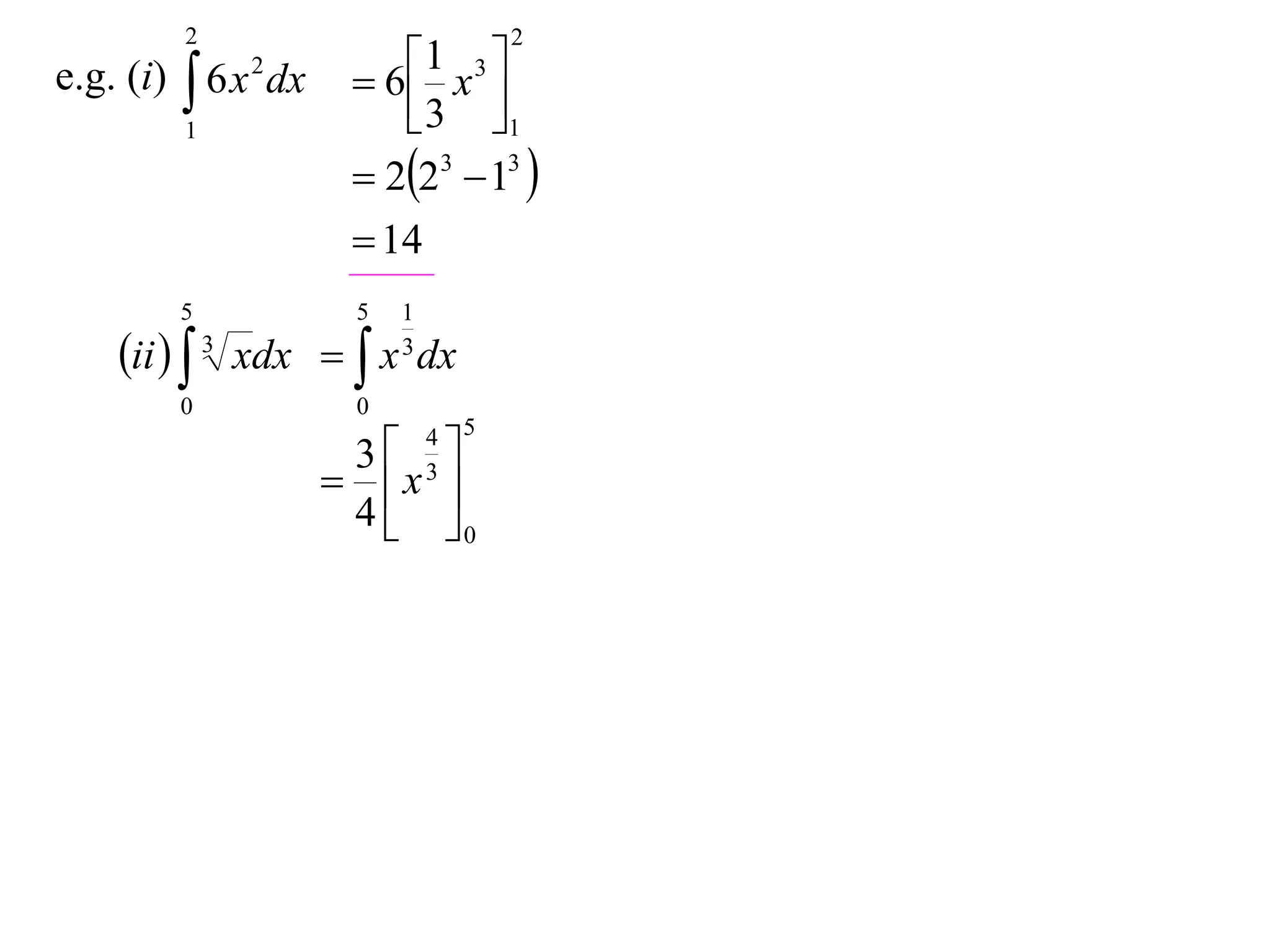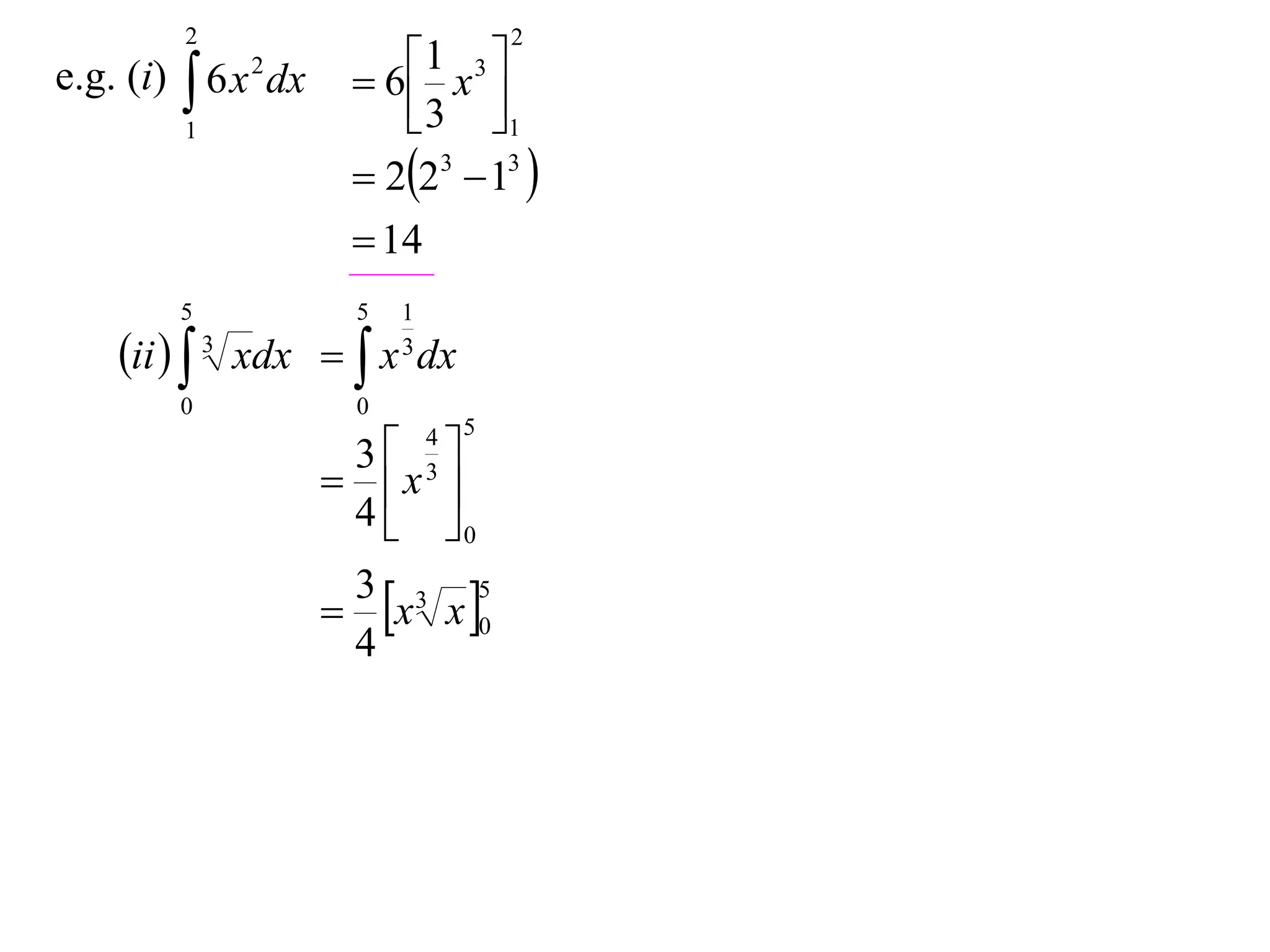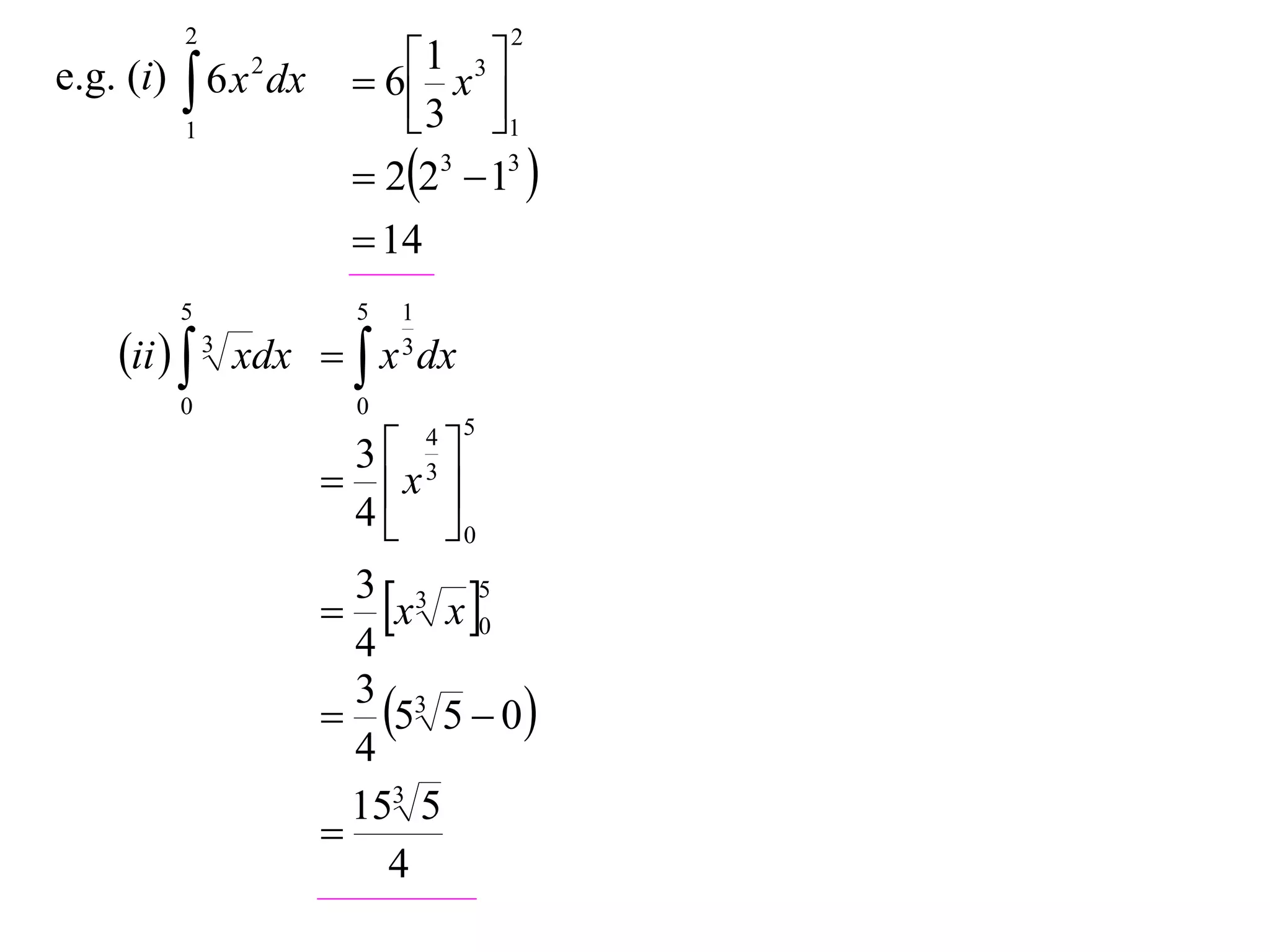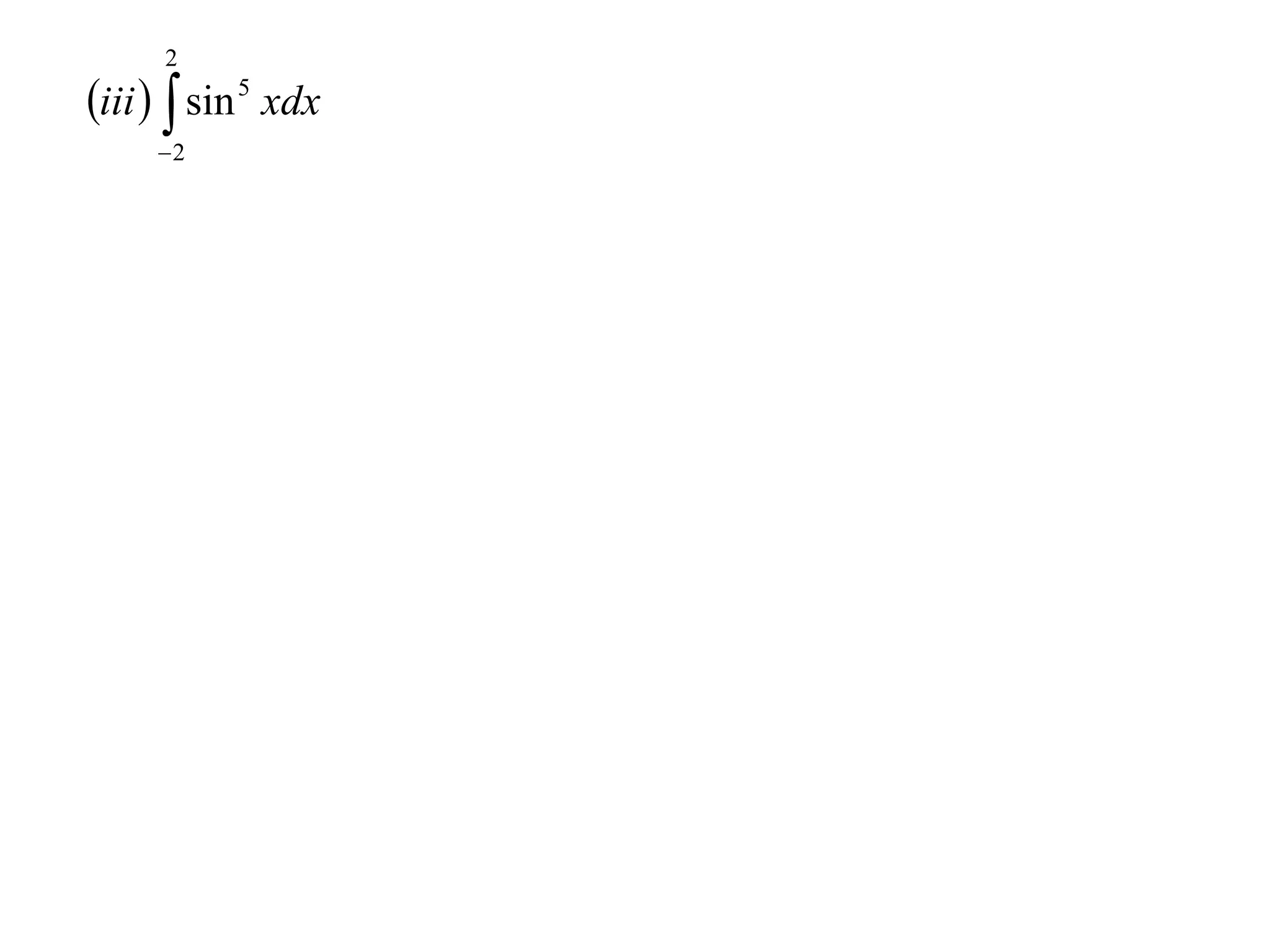The document discusses 8 properties of definite integrals: 1) Integrating polynomials results in a fraction. 2) Constants can be factored out of integrals. 3) Integrals of sums are equal to the sum of integrals. 4) Splitting an integral range results in the sum of the integrals. 5) Integrals of positive functions over a range are positive, and negative if the function is negative. 6) Integrals can be compared based on the relative values of the integrands. 7) Changing the limits of integration flips the sign of the integral. 8) Integrals of odd functions over a symmetric range are zero, and integrals of even functions are twice the integral over

1. Properties Of
Definite Integral

2. Properties Of
Definite Integral
1 a
b
n 1
b
x 
x dx  
n  1 a


n

3. Properties Of
Definite Integral
1 a
b
n 1
b
x 
x dx  
n  1 a


n
2 a kf  x dx k a f  x dx
b
b
can only factorise constants 

4. Properties Of
Definite Integral
1 a
b
n 1
b
x 
x dx  
n  1 a


n
2 a kf  x dx k a f  x dx
b
b
can only factorise constants 
3 a  f  x   g  x dx  a f  x dx  a g  x dx
b
b
b

5. Properties Of
Definite Integral
1 a
b
n 1
b
x 
x dx  
n  1 a


n
can only factorise constants 
2 a kf  x dx k a f  x dx
b
b
3 a  f  x   g  x dx  a f  x dx  a g  x dx
b
b
b
4 a f  x dx  a f  x dx  c f  x dx
b
c
b

6. 5 a x n dx  0
b

7. 5 a x n dx  0
b
, if f  x   0 for a  x  b

8. 5 a x n dx  0
b
0
, if f  x   0 for a  x  b
, if f  x   0 for a  x  b

9. 5 a x n dx  0
b
, if f  x   0 for a  x  b
, if f  x   0 for a  x  b
0
6 a f  x dx  a g  x dx
b
b

10. 5 a x n dx  0
b
, if f  x   0 for a  x  b
, if f  x   0 for a  x  b
0
6 a f  x dx  a g  x dx
b
b
, if f  x   g  x  for a  x  b

11. 5 a x n dx  0
b
, if f  x   0 for a  x  b
, if f  x   0 for a  x  b
0
6 a f  x dx  a g  x dx
b
b
7 a f  x dx   b f  x dx
b
a
, if f  x   g  x  for a  x  b

12. 5 a x n dx  0
b
, if f  x   0 for a  x  b
, if f  x   0 for a  x  b
0
6 a f  x dx  a g  x dx
b
b
, if f  x   g  x  for a  x  b
7 a f  x dx   b f  x dx
b
a
8  f  x   0 ,
a
a
if f  x  is odd

13. 5 a x n dx  0
b
, if f  x   0 for a  x  b
, if f  x   0 for a  x  b
0
6 a f  x dx  a g  x dx
b
b
, if f  x   g  x  for a  x  b
7 a f  x dx   b f  x dx
b
a
a
8  f  x   0 ,
a
a
a
a
0
if f  x  is odd
9  f  x   2 f  x  ,
if f  x  is even

14. 5 a x n dx  0
b
, if f  x   0 for a  x  b
, if f  x   0 for a  x  b
0
6 a f  x dx  a g  x dx
b
b
, if f  x   g  x  for a  x  b
7 a f  x dx   b f  x dx
b
a
a
8  f  x   0 ,
a
a
a
a
0
if f  x  is odd
9  f  x   2 f  x  ,
if f  x  is even
NOTE :
odd  odd  even
odd  even  odd
even  even  even

15. 2
e.g. (i)  6 x 2 dx
1

16. 2
e.g. (i)  6 x 2 dx
1
2
1 x 3 
 6
 3 1


17. 2
e.g. (i)  6 x 2 dx
1
2
1 x 3 
 6
 3 1

 223  13 
 14

18. 2
e.g. (i)  6 x 2 dx
1
5
ii   3 xdx
0
2
1 x 3 
 6
 3 1

 223  13 
 14

19. 2
e.g. (i)  6 x 2 dx
1
2
1 x 3 
 6
 3 1

 223  13 
 14
5
5
0
0
1
3
ii   3 xdx   x dx

20. 2
e.g. (i)  6 x 2 dx
1
2
1 x 3 
 6
 3 1

 223  13 
 14
5
5
0
0
1
3
ii   3 xdx   x dx
5
3 
 x 
4  0
4
3

21. 2
e.g. (i)  6 x 2 dx
1
2
1 x 3 
 6
 3 1

 223  13 
 14
5
5
0
0
1
3
ii   3 xdx   x dx
5
3 
 x 
4  0
3 3 5
 x x 0
4
4
3

22. 2
e.g. (i)  6 x 2 dx
1
2
1 x 3 
 6
 3 1

 223  13 
 14
5
5
0
0
1
3
ii   3 xdx   x dx
5
3 
 x 
4  0
3 3 5
 x x 0
4
3 3
 5 5  0 
4
153 5

4
4
3

23. 2
iii   sin 5 xdx
2

24. 2
iii   sin 5 xdx  0
2
odd function 5  odd function

25. 2
iii   sin 5 xdx  0
2
1
iv  x 3  2 x 2  x  1dx
1
odd function 5  odd function

26. 2
iii   sin 5 xdx  0
odd function 5  odd function
2
1
1
1
0
iv  x 3  2 x 2  x  1dx  2 2 x 2  1dx

27. 2
iii   sin 5 xdx  0
odd function 5  odd function
2
1
1
1
0
iv  x 3  2 x 2  x  1dx  2 2 x 2  1dx
1
 2 x3  x
 2
0
3


28. 2
iii   sin 5 xdx  0
odd function 5  odd function
2
1
1
1
0
iv  x 3  2 x 2  x  1dx  2 2 x 2  1dx
1
 2 x3  x
 2
0
3

 2 1 3  1  0
 2  

3

10

3

29. 2
iii   sin 5 xdx  0
odd function 5  odd function
2
1
1
1
0
iv  x 3  2 x 2  x  1dx  2 2 x 2  1dx
1
 2 x3  x
 2
0
3

 2 1 3  1  0
 2  

3

10

3
Exercise 11C; 1bce, 2adf, 3ab (i, iii), 4bcf, 5, 6ac, 7df, 8b,
12b, 13*