The document discusses approximations of areas under curves using the trapezoidal rule. It shows the general trapezoidal rule formula for approximating the area under a curve between two points by dividing the area into trapezoids. An example is provided to demonstrate applying the trapezoidal rule with 4 intervals to estimate the area under the curve y = (4 - x)^(1/2) from x = 0 to x = 2, giving an answer of 2.996 units^2 correct to 3 decimal places.

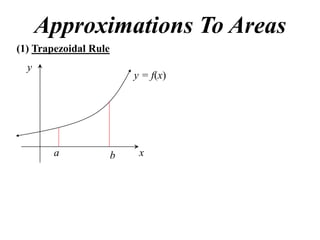
1. Approximations To Areas
(1) Trapezoidal Rule
y
y = f(x)
a b x

2. Approximations To Areas
(1) Trapezoidal Rule
y
y = f(x)
a b x

3. Approximations To Areas
(1) Trapezoidal Rule
y
y = f(x) ba
A  f a   f b 
2
a b x

4. Approximations To Areas
(1) Trapezoidal Rule
y
y = f(x) ba
A  f a   f b 
2
y y = f(x)
a b x
a b x

5. Approximations To Areas
(1) Trapezoidal Rule
y
y = f(x) ba
A  f a   f b 
2
y y = f(x)
a b x
a c b x

6. Approximations To Areas
(1) Trapezoidal Rule
y
y = f(x) ba
A  f a   f b 
2
y y = f(x)
a b x
ca bc
A  f a   f c    f c   f b 
2 2
a c b x

7. Approximations To Areas
(1) Trapezoidal Rule
y
y = f(x) ba
A  f a   f b 
2
y y = f(x)
a b x
ca bc
A  f a   f c    f c   f b 
2 2
ca
  f a   2 f c   f b 
2
a c b x

8. y
y = f(x)
a b x

9. y
y = f(x)
a c d b x

10. y
y = f(x)
ca d c
A  f a   f c    f c   f d 
2 2
bd
  f d   f b 
2
a c d b x

11. y
y = f(x)
ca d c
A  f a   f c    f c   f d 
2 2
bd
  f d   f b 
2
a c d b x  c  a  f a   2 f c   2 f d   f b 
2

12. y
y = f(x)
ca d c
A  f a   f c    f c   f d 
2 2
bd
  f d   f b 
2
a c d b x  c  a  f a   2 f c   2 f d   f b 
2
In general;

13. y
y = f(x)
ca d c
A  f a   f c    f c   f d 
2 2
bd
  f d   f b 
2
a c d b x  c  a  f a   2 f c   2 f d   f b 
2
In general; b
Area   f  x dx
a

14. y
y = f(x)
ca d c
A  f a   f c    f c   f d 
2 2
bd
  f d   f b 
2
a c d b x  c  a  f a   2 f c   2 f d   f b 
2
In general; b
Area   f  x dx
a
h
 y0  2 yothers  yn 
2

15. y
y = f(x)
ca d c
A  f a   f c    f c   f d 
2 2
bd
  f d   f b 
2
a c d b x  c  a  f a   2 f c   2 f d   f b 
2
In general; b
Area   f  x dx
a
h
 y0  2 yothers  yn 
2
ba
where h 
n
n  number of trapeziums

16. y
y = f(x)
ca d c
A  f a   f c    f c   f d 
2 2
bd
  f d   f b 
2
a c d b x  c  a  f a   2 f c   2 f d   f b 
2
In general; b
Area   f  x dx
a
h
 y0  2 yothers  yn  NOTE: there is
2
ba always one more
where h  function value
n
than interval
n  number of trapeziums

17. e.g. Use the Trapezoida l Rule with 4 intervals to estimate the
area under the curve y  4  x  , between x  0 and x  2
1
2 2
correct to 3 decimal points 

18. e.g. Use the Trapezoida l Rule with 4 intervals to estimate the
area under the curve y  4  x  , between x  0 and x  2
1
2 2
correct to 3 decimal points 
ba
h
n
20

4
 0.5

19. e.g. Use the Trapezoida l Rule with 4 intervals to estimate the
area under the curve y  4  x  , between x  0 and x  2
1
2 2
correct to 3 decimal points 
ba
h
n x 0 0.5 1 1.5 2
20 y 2 1.9365 1.7321 1.3229 0

4
 0.5

20. e.g. Use the Trapezoida l Rule with 4 intervals to estimate the
area under the curve y  4  x  , between x  0 and x  2
1
2 2
correct to 3 decimal points 
ba
h
n x 0 0.5 1 1.5 2
20 y 2 1.9365 1.7321 1.3229 0
 h
4 Area  y0  2 yothers  yn 
 0.5 2

21. e.g. Use the Trapezoida l Rule with 4 intervals to estimate the
area under the curve y  4  x  , between x  0 and x  2
1
2 2
correct to 3 decimal points 
ba 1 1
h
n x 0 0.5 1 1.5 2
20 y 2 1.9365 1.7321 1.3229 0
 h
4 Area  y0  2 yothers  yn 
 0.5 2

22. e.g. Use the Trapezoida l Rule with 4 intervals to estimate the
area under the curve y  4  x  , between x  0 and x  2
1
2 2
correct to 3 decimal points 
ba 1 2 2 2 1
h
n x 0 0.5 1 1.5 2
20 y 2 1.9365 1.7321 1.3229 0
 h
4 Area  y0  2 yothers  yn 
 0.5 2

23. e.g. Use the Trapezoida l Rule with 4 intervals to estimate the
area under the curve y  4  x  , between x  0 and x  2
1
2 2
correct to 3 decimal points 
ba 1 2 2 2 1
h
n x 0 0.5 1 1.5 2
20 y 2 1.9365 1.7321 1.3229 0
 h
4 Area  y0  2 yothers  yn 
 0.5 2
0.5
 2  21.9365  1.7321  1.3229  0
2
 2.996 units 2

24. e.g. Use the Trapezoida l Rule with 4 intervals to estimate the
area under the curve y  4  x  , between x  0 and x  2
1
2 2
correct to 3 decimal points 
ba 1 2 2 2 1
h
n x 0 0.5 1 1.5 2
20 y 2 1.9365 1.7321 1.3229 0
 h
4 Area  y0  2 yothers  yn 
 0.5 2
0.5
 2  21.9365  1.7321  1.3229  0
2
 2.996 units 2 exact value  π 

25. e.g. Use the Trapezoida l Rule with 4 intervals to estimate the
area under the curve y  4  x  , between x  0 and x  2
1
2 2
correct to 3 decimal points 
ba 1 2 2 2 1
h
n x 0 0.5 1 1.5 2
20 y 2 1.9365 1.7321 1.3229 0
 h
4 Area  y0  2 yothers  yn 
 0.5 2
0.5
 2  21.9365  1.7321  1.3229  0
2
 2.996 units 2 exact value  π 
3.142  2.996
% error  100
3.142
 4.6%

26. (2) Simpson’s Rule

27. (2) Simpson’s Rule
b
Area   f  x dx
a

28. (2) Simpson’s Rule
b
Area   f  x dx
a
h
 y0  4 yodd  2 yeven  yn 
3

29. (2) Simpson’s Rule
b
Area   f  x dx
a
h
 y0  4 yodd  2 yeven  yn 
3
ba
where h 
n
n  number of intervals

30. (2) Simpson’s Rule
b
Area   f  x dx
a
h
 y0  4 yodd  2 yeven  yn 
3
ba
where h 
n
n  number of intervals
e.g.
x 0 0.5 1 1.5 2
y 2 1.9365 1.7321 1.3229 0

31. (2) Simpson’s Rule
b
Area   f  x dx
a
h
 y0  4 yodd  2 yeven  yn 
3
ba
where h 
n
n  number of intervals
e.g.
x 0 0.5 1 1.5 2
y 2 1.9365 1.7321 1.3229 0
h
Area  y0  4 yodd  2 yeven  yn 
3

32. (2) Simpson’s Rule
b
Area   f  x dx
a
h
 y0  4 yodd  2 yeven  yn 
3
ba
where h 
n
n  number of intervals
e.g. 1 1
x 0 0.5 1 1.5 2
y 2 1.9365 1.7321 1.3229 0
h
Area  y0  4 yodd  2 yeven  yn 
3

33. (2) Simpson’s Rule
b
Area   f  x dx
a
h
 y0  4 yodd  2 yeven  yn 
3
ba
where h 
n
n  number of intervals
e.g. 1 4 4 1
x 0 0.5 1 1.5 2
y 2 1.9365 1.7321 1.3229 0
h
Area  y0  4 yodd  2 yeven  yn 
3

34. (2) Simpson’s Rule
b
Area   f  x dx
a
h
 y0  4 yodd  2 yeven  yn 
3
ba
where h 
n
n  number of intervals
e.g. 1 4 2 4 1
x 0 0.5 1 1.5 2
y 2 1.9365 1.7321 1.3229 0
h
Area  y0  4 yodd  2 yeven  yn 
3

35. (2) Simpson’s Rule
b
Area   f  x dx
a
h
 y0  4 yodd  2 yeven  yn 
3
ba
where h 
n
n  number of intervals
e.g. 1 4 2 4 1
x 0 0.5 1 1.5 2
y 2 1.9365 1.7321 1.3229 0
h
Area  y0  4 yodd  2 yeven  yn 
3
0.5
 2  41.9365  1.3229  21.7321  0
3
 3.084 units 2

36. (2) Simpson’s Rule
b
Area   f  x dx
a
h
 y0  4 yodd  2 yeven  yn 
3
ba
where h 
n
n  number of intervals
e.g. 1 4 2 4 1
x 0 0.5 1 1.5 2
y 2 1.9365 1.7321 1.3229 0
h
Area  y0  4 yodd  2 yeven  yn 
3
0.5
 2  41.9365  1.3229  21.7321  0 3.142  3.084
3 % error  100
 3.084 units 2 3.142
 1.8%

37. Alternative working out!!!
(1) Trapezoidal Rule

38. Alternative working out!!!
(1) Trapezoidal Rule
1 2 2 2 1
x 0 0.5 1 1.5 2
y 2 1.9365 1.7321 1.3229 0

39. Alternative working out!!!
(1) Trapezoidal Rule
1 2 2 2 1
x 0 0.5 1 1.5 2
y 2 1.9365 1.7321 1.3229 0
2  2 1.9365  1.7321  1.3229   0
Area    2  0
1 2  2  2 1
 2.996 units 2

40. (2) Simpson’s Rule
1 4 2 4 1
x 0 0.5 1 1.5 2
y 2 1.9365 1.7321 1.3229 0

41. (2) Simpson’s Rule
1 4 2 4 1
x 0 0.5 1 1.5 2
y 2 1.9365 1.7321 1.3229 0
2  4 1.9365  1.3229   2 1.7321  0
Area    2  0
1 4  2  4 1
 3.084 units 2

42. (2) Simpson’s Rule
1 4 2 4 1
x 0 0.5 1 1.5 2
y 2 1.9365 1.7321 1.3229 0
2  4 1.9365  1.3229   2 1.7321  0
Area    2  0
1 4  2  4 1
 3.084 units 2
Exercise 11I; odds
Exercise 11J; evens