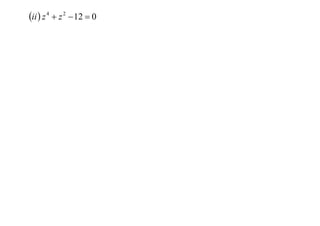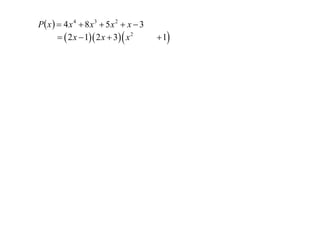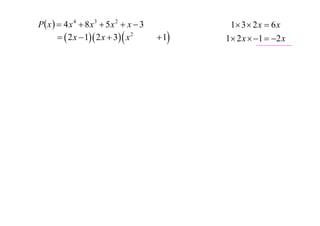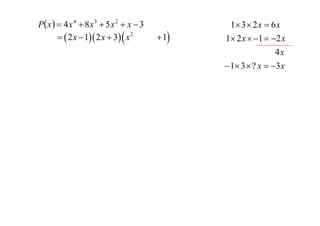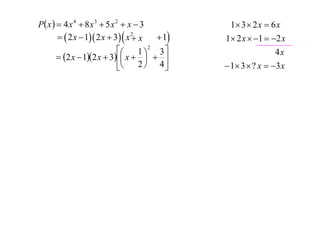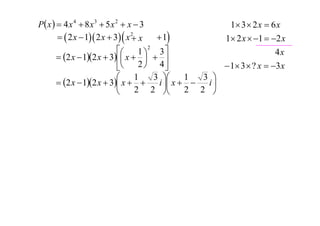The document discusses factorizing complex expressions. The main points are: - If a polynomial's coefficients are real, its roots will appear in complex conjugate pairs. - Any polynomial of degree n can be factorized into a mixture of quadratic and linear factors over real numbers, or into n linear factors over complex numbers. - Odd degree polynomials must have at least one real root. - Examples of factorizing polynomials over both real and complex numbers are provided.

1. Factorising Complex
Expressions

2. Factorising Complex
Expressions
If a polynomial’s coefficients are all real then the roots will appear
in complex conjugate pairs.

3. Factorising Complex
Expressions
If a polynomial’s coefficients are all real then the roots will appear
in complex conjugate pairs.
Every polynomial of degree n can be;
• factorised as a mixture of quadratic and linear factors over the
real field

4. Factorising Complex
Expressions
If a polynomial’s coefficients are all real then the roots will appear
in complex conjugate pairs.
Every polynomial of degree n can be;
• factorised as a mixture of quadratic and linear factors over the
real field
• factorised to n linear factors over the complex field

5. Factorising Complex
Expressions
If a polynomial’s coefficients are all real then the roots will appear
in complex conjugate pairs.
Every polynomial of degree n can be;
• factorised as a mixture of quadratic and linear factors over the
real field
• factorised to n linear factors over the complex field
NOTE: odd ordered polynomials must have a real root

6. Factorising Complex
Expressions
If a polynomial’s coefficients are all real then the roots will appear
in complex conjugate pairs.
Every polynomial of degree n can be;
• factorised as a mixture of quadratic and linear factors over the
real field
• factorised to n linear factors over the complex field
NOTE: odd ordered polynomials must have a real root
e.g . i  x 2  2 x  2

7. Factorising Complex
Expressions
If a polynomial’s coefficients are all real then the roots will appear
in complex conjugate pairs.
Every polynomial of degree n can be;
• factorised as a mixture of quadratic and linear factors over the
real field
• factorised to n linear factors over the complex field
NOTE: odd ordered polynomials must have a real root
e.g . i  x 2  2 x  2   x  12  1

8. Factorising Complex
Expressions
If a polynomial’s coefficients are all real then the roots will appear
in complex conjugate pairs.
Every polynomial of degree n can be;
• factorised as a mixture of quadratic and linear factors over the
real field
• factorised to n linear factors over the complex field
NOTE: odd ordered polynomials must have a real root
e.g . i  x 2  2 x  2   x  12  1
  x  1  i  x  1  i 

9. ii  z 4  z 2  12  0

10. ii  z 4  z 2  12  0
z
2
 3z 2  4   0

11. ii  z 4  z 2  12  0
z  3z  4  0
z  3 z  3z  4  0
2
2
2
factorised over Real numbers

12. ii  z 4  z 2  12  0
z  3z  4  0
factorised over Real numbers
z  3 z  3z  4  0
z  3 z  3 z  2i  z  2i   0 factorised over Complex numbers
2
2
2

13. ii  z 4  z 2  12  0
z  3z  4  0
factorised over Real numbers
z  3 z  3z  4  0
z  3 z  3 z  2i  z  2i   0 factorised over Complex numbers
2
2
2
z   3 or z  2i

14. ii  z 4  z 2  12  0
z  3z  4  0
factorised over Real numbers
z  3 z  3z  4  0
z  3 z  3 z  2i  z  2i   0 factorised over Complex numbers
2
2
2
z   3 or z  2i
If (x – a) is a factor of P(x), then P(a) = 0
b
If (ax – b) is a factor of P(x), then P  = 0
a

15. ii  z 4  z 2  12  0
z  3z  4  0
factorised over Real numbers
z  3 z  3z  4  0
z  3 z  3 z  2i  z  2i   0 factorised over Complex numbers
2
2
2
z   3 or z  2i
If (x – a) is a factor of P(x), then P(a) = 0
b
If (ax – b) is a factor of P(x), then P  = 0
a
iii  Factorise 2 x 3  3x 2  8 x  5

16. ii  z 4  z 2  12  0
z  3z  4  0
factorised over Real numbers
z  3 z  3z  4  0
z  3 z  3 z  2i  z  2i   0 factorised over Complex numbers
2
2
2
z   3 or z  2i
If (x – a) is a factor of P(x), then P(a) = 0
b
If (ax – b) is a factor of P(x), then P  = 0
a
iii  Factorise 2 x 3  3x 2  8 x  5
as it is a cubic it must have a real factor

17. ii  z 4  z 2  12  0
z  3z  4  0
factorised over Real numbers
z  3 z  3z  4  0
z  3 z  3 z  2i  z  2i   0 factorised over Complex numbers
2
2
2
z   3 or z  2i
If (x – a) is a factor of P(x), then P(a) = 0
b
If (ax – b) is a factor of P(x), then P  = 0
a
iii  Factorise 2 x 3  3x 2  8 x  5
as it is a cubic it must have a real factor
3
2
1  1
1


 1 5
P   2    3   8 
 2  2
 2
 2
1 3
   45
4 4
0

18. ii  z 4  z 2  12  0
z  3z  4  0
factorised over Real numbers
z  3 z  3z  4  0
z  3 z  3 z  2i  z  2i   0 factorised over Complex numbers
2
2
2
z   3 or z  2i
If (x – a) is a factor of P(x), then P(a) = 0
b
If (ax – b) is a factor of P(x), then P  = 0
a
iii  Factorise 2 x 3  3x 2  8 x  5
as it is a cubic it must have a real factor
3
2
1  1
1


 1 5
 2 x3  3x 2  8 x  5
P   2    3   8 
 2  2
 2
 2
  2 x  1  x 2  2 x  5 
1 3
   45
4 4
0

19. ii  z 4  z 2  12  0
z  3z  4  0
factorised over Real numbers
z  3 z  3z  4  0
z  3 z  3 z  2i  z  2i   0 factorised over Complex numbers
2
2
2
z   3 or z  2i
If (x – a) is a factor of P(x), then P(a) = 0
b
If (ax – b) is a factor of P(x), then P  = 0
a
iii  Factorise 2 x 3  3x 2  8 x  5
as it is a cubic it must have a real factor
3
2
1  1
1


 1 5
 2 x3  3x 2  8 x  5
P   2    3   8 
 2  2
 2
 2
  2 x  1  x 2  2 x  5 
1 3
   45
2
 2 x  1  x  1  4
4 4
0



20. ii  z 4  z 2  12  0
z  3z  4  0
factorised over Real numbers
z  3 z  3z  4  0
z  3 z  3 z  2i  z  2i   0 factorised over Complex numbers
2
2
2
z   3 or z  2i
If (x – a) is a factor of P(x), then P(a) = 0
b
If (ax – b) is a factor of P(x), then P  = 0
a
iii  Factorise 2 x 3  3x 2  8 x  5
as it is a cubic it must have a real factor
3
2
1  1
1


 1 5
 2 x3  3x 2  8 x  5
P   2    3   8 
 2  2
 2
 2
  2 x  1  x 2  2 x  5 
1 3
   45
2
 2 x  1  x  1  4
4 4
 2 x  1 x  1  2i  x  1  2i 
0



21. (iv) Given that P x   4 x 4  8 x 3  5 x 2  x  3 has two rational zeros,
find these zeros and factorise P(x) over the complex field.

22. (iv) Given that P x   4 x 4  8 x 3  5 x 2  x  3 has two rational zeros,
find these zeros and factorise P(x) over the complex field.
 1   4 1   8 1   5 1   1  3
P       
 2   16   8   4  2
0
 2 x  1 is a factor

23. (iv) Given that P x   4 x 4  8 x 3  5 x 2  x  3 has two rational zeros,
find these zeros and factorise P(x) over the complex field.
 1   4 1   8 1   5 1   1  3
P       
 2   16   8   4  2
0
 2 x  1 is a factor
P x   2 x  12 x 3
 3

24. (iv) Given that P x   4 x 4  8 x 3  5 x 2  x  3 has two rational zeros,
find these zeros and factorise P(x) over the complex field.
 1   4 1   8 1   5 1   1  3
P       
 2   16   8   4  2
0
 2 x  1 is a factor
P x   2 x  12 x 3
 5 x  3

25. (iv) Given that P x   4 x 4  8 x 3  5 x 2  x  3 has two rational zeros,
find these zeros and factorise P(x) over the complex field.
 1   4 1   8 1   5 1   1  3
P       
 2   16   8   4  2
0
 2 x  1 is a factor
P x   2 x  12 x 3 5x 2  5 x  3

26. (iv) Given that P x   4 x 4  8 x 3  5 x 2  x  3 has two rational zeros,
find these zeros and factorise P(x) over the complex field.
 1   4 1   8 1   5 1   1  3
P       
 2   16   8   4  2
0
 2 x  1 is a factor
P x   2 x  12 x 3 5x 2  5 x  3
 3    27   9   3 
P    2
  5   5    3
 2  8   4  2
0

27. (iv) Given that P x   4 x 4  8 x 3  5 x 2  x  3 has two rational zeros,
find these zeros and factorise P(x) over the complex field.
 1   4 1   8 1   5 1   1  3
P       
 2   16   8   4  2
0
 2 x  1 is a factor
P x   2 x  12 x 3 5x 2  5 x  3
 3    27   9   3 
P    2
  5   5    3
 2  8   4  2
0
 2 x  3 is a factor
3
1
 rational zeros are and 2
2

28. P x   4 x 4  8 x 3  5 x 2  x  3

29. P x   4 x 4  8 x 3  5 x 2  x  3
  2 x  1 2 x  3  x 2
 1

30. P x   4 x 4  8 x 3  5 x 2  x  3
  2 x  1 2 x  3  x 2
 1
1 3  2 x  6 x
1 2 x  1  2 x

31. P x   4 x 4  8 x 3  5 x 2  x  3
  2 x  1 2 x  3  x 2
 1
1 3  2 x  6 x
1 2 x  1  2 x
4x
 1 3  ? x  3 x

32. P x   4 x 4  8 x 3  5 x 2  x  3
  2 x  1 2 x  3  x 2 x
 1
1 3  2 x  6 x
1 2 x  1  2 x
4x
 1 3  ? x  3 x

33. P x   4 x 4  8 x 3  5 x 2  x  3
  2 x  1 2 x  3  x 2 x
 1
2

1  3
 2 x  12 x  3 x    
2  4

1 3  2 x  6 x
1 2 x  1  2 x
4x
 1 3  ? x  3 x

34. P x   4 x 4  8 x 3  5 x 2  x  3
1 3  2 x  6 x
  2 x  1 2 x  3  x 2 x
 1
1 2 x  1  2 x
2

1  3
4x
 2 x  12 x  3 x    
2  4
 1 3  ? x  3 x

1
3 
1
3 

 2 x  12 x  3 x  
i  x  
i
2 2 
2 2 


35. P x   4 x 4  8 x 3  5 x 2  x  3
1 3  2 x  6 x
  2 x  1 2 x  3  x 2 x
 1
1 2 x  1  2 x
2

1  3
4x
 2 x  12 x  3 x    
2  4
 1 3  ? x  3 x

1
3 
1
3 

 2 x  12 x  3 x  
i  x  
i
2 2 
2 2 

Cambridge: Exercise 5A; 1b, 2, 3, 5, 6, 7b, 8, 9, 10, 12 to 15