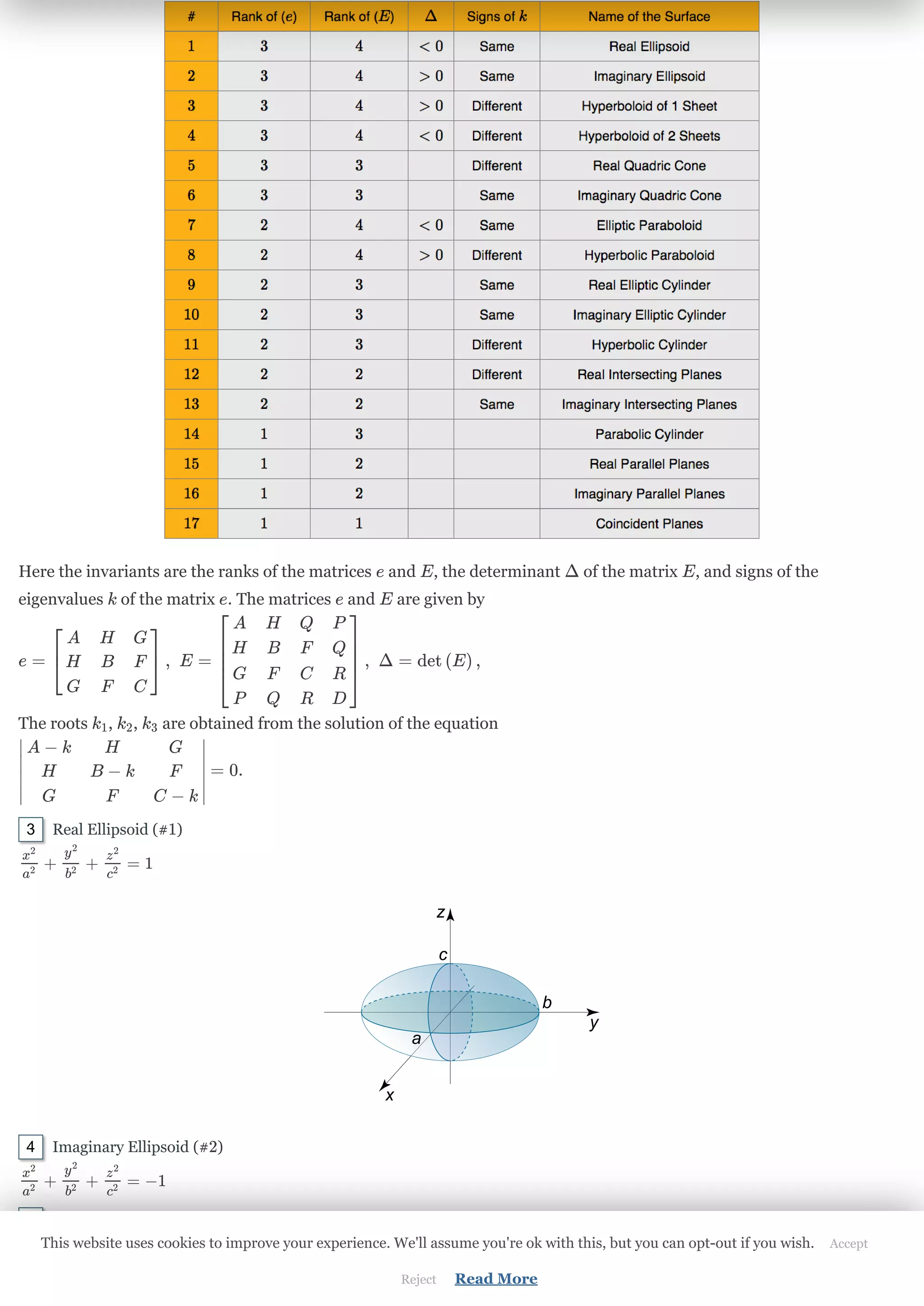
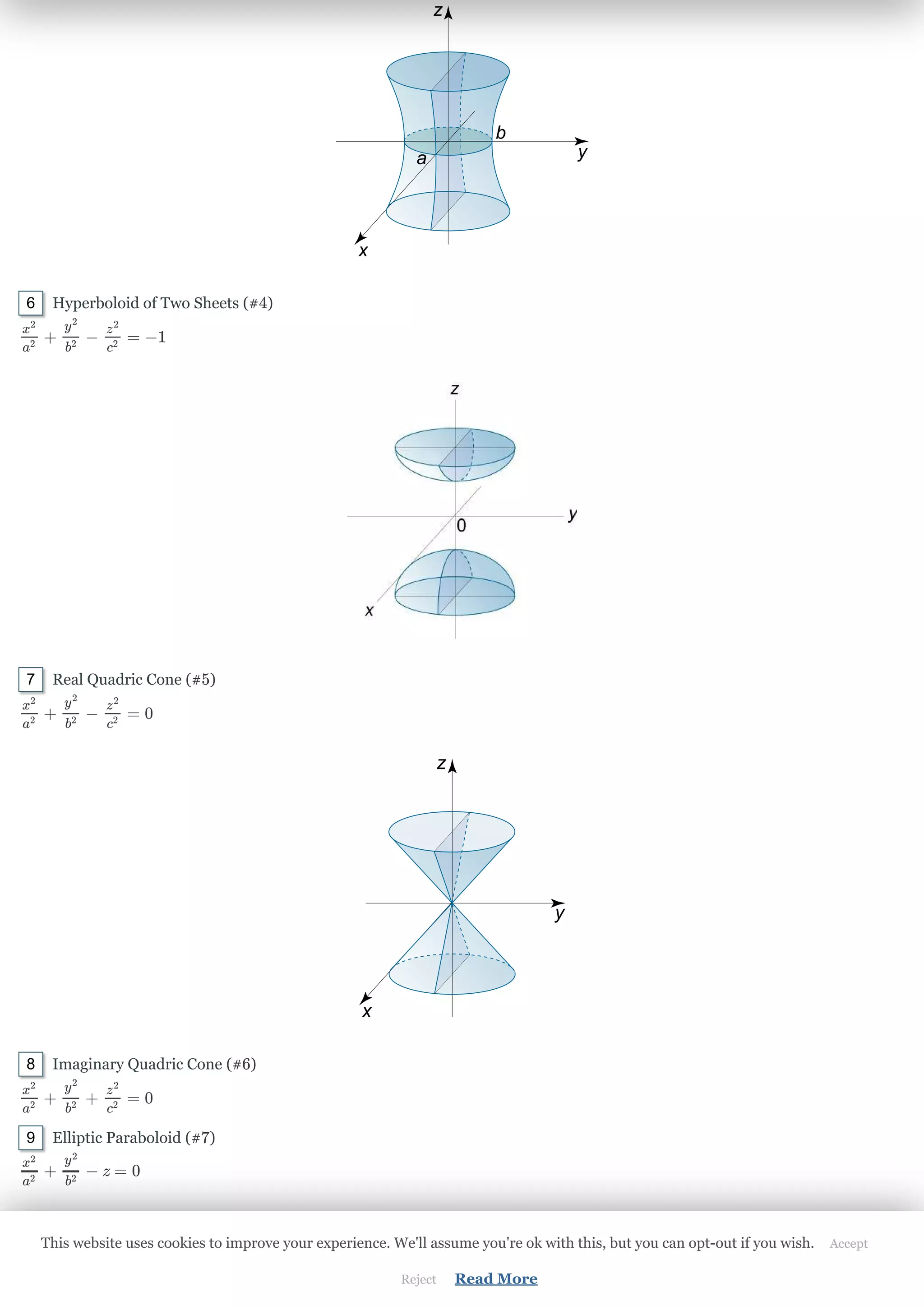
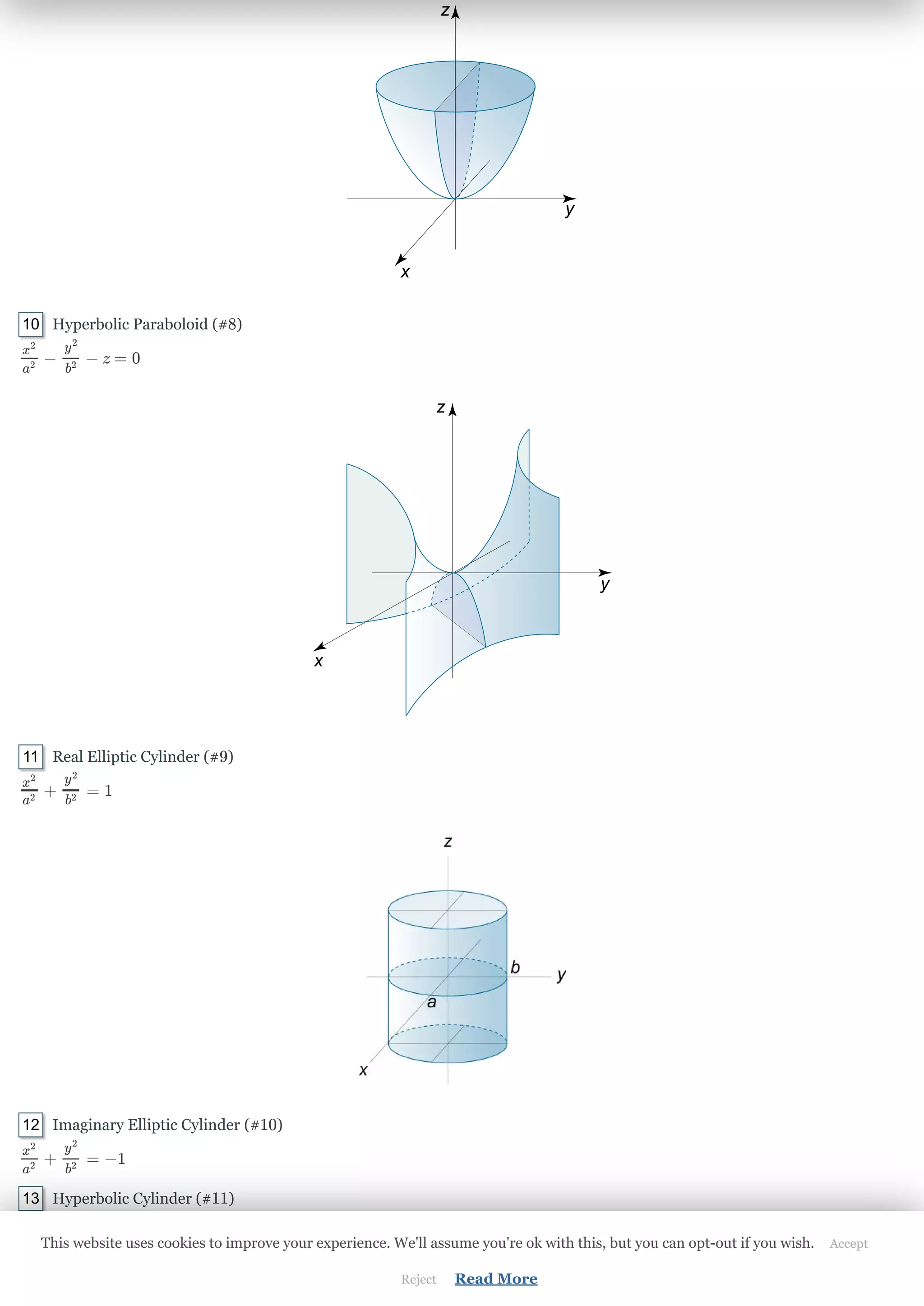
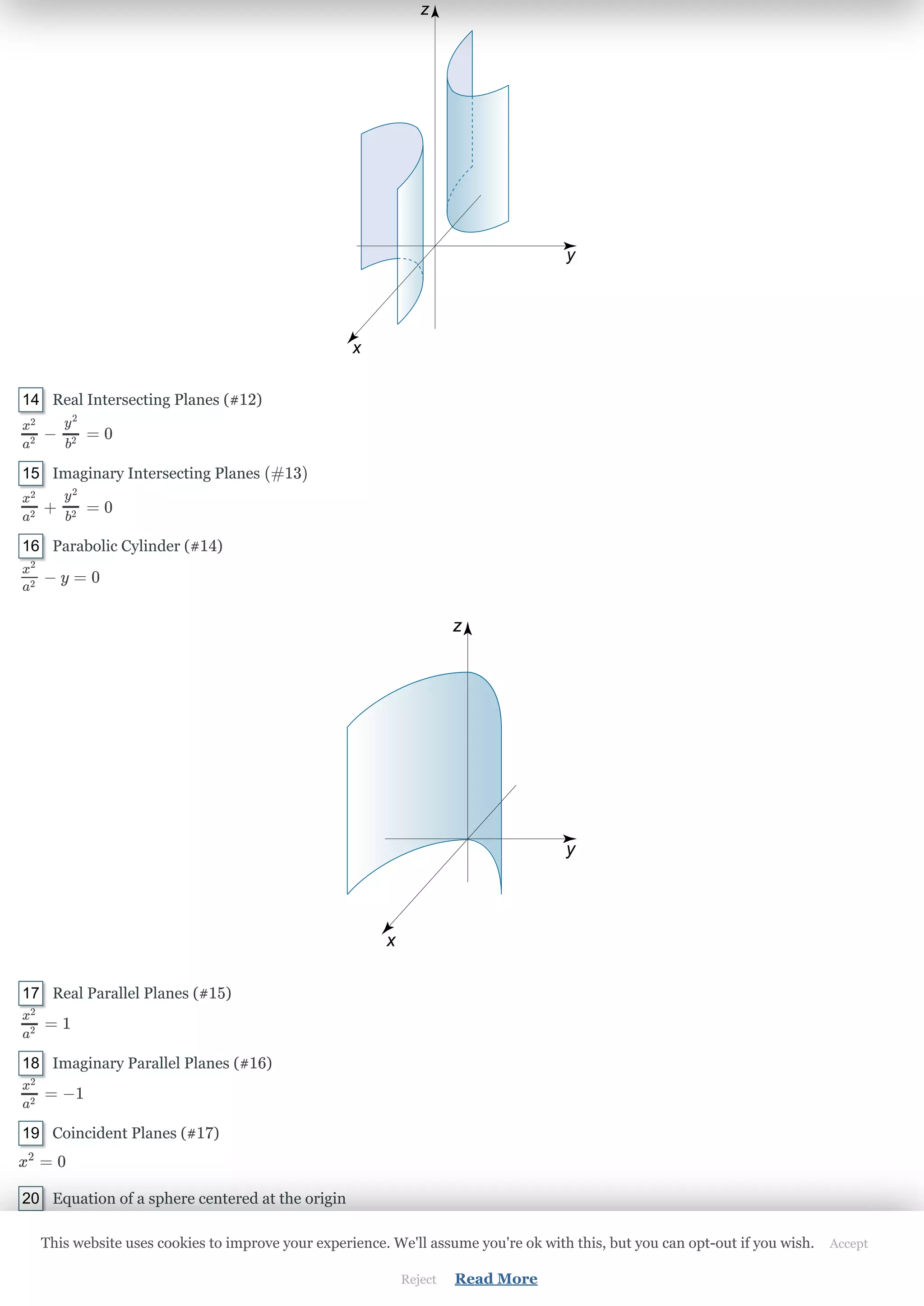
The document discusses quadric surfaces and spheres. It provides the general equation for quadric surfaces using Cartesian coordinates and coefficients. It describes how quadric surfaces are classified based on invariants including the ranks of matrices e and E and the determinant of E. Several specific types of quadric surfaces are defined by their invariants, including ellipsoids, hyperboloids, paraboloids, cylinders, cones, and planes. It also provides equations for spheres in standard, diameter, and four point forms, and describes how to derive the center and radius from the general quadratic equation of a sphere.

1. Point coordinates of the quadric surfaces: x,
y, z, x1, y1, z1, …
Real numbers: A, B, C, … , a, b, c, k1, k2, k3
Invariants: e, E, Δ
Radius of a sphere: R
Center of a sphere: (a, b, c)
FormulasFormulas
Analytic Geometry
Quadric Surfaces
1 General equation of a quadric surface
Ax
2
+ By
2
+ Cz
2
+ 2F yz + 2Gzx + 2Hxy + 2P x + 2Qy + 2Rz + D = 0,
where x, y, z are the Cartesian coordinates of the points of the surface, A, B, C, … are real numbers.
2 Classification of quadric surfaces
This classification is based on invariants of the quadric surfaces. Invariants are special expressions composed of the coefficients
of the general equation which do not change under parallel translation or rotation of the coordinate system. In total, there are 17
different (canonical) classes of the quadric surfaces.
Math24
 Menu
Arc-Flash Case Studies
Protect Your Workforce And Equipment With Fast Arc-
Flash Protection.
OPEN

This website uses cookies to improve your experience. We'll assume you're ok with this, but you can opt-out if you wish.
Read More
Accept
Reject

2. Here the invariants are the ranks of the matrices e and E, the determinant Δ of the matrix E, and signs of the
eigenvalues k of the matrix e. The matrices e and E are given by
e =
⎡
⎢
⎣
A H G
H B F
G F C
⎤
⎥
⎦
, E =
⎡
⎢
⎢
⎢
⎢
⎣
A H Q P
H B F Q
G F C R
P Q R D
⎤
⎥
⎥
⎥
⎥
⎦
, Δ = det (E) ,
The roots k1, k2, k3 are obtained from the solution of the equation
∣
∣
∣
∣
A − k H G
H B − k F
G F C − k
∣
∣
∣
∣
= 0.
3 Real Ellipsoid (#1)
+ + = 1
4 Imaginary Ellipsoid (#2)
+ + = −1
5 Hyperboloid of One Sheet (#3)
+ − = 1
x
2
a
2
y
2
b
2
z
2
c
2
x
2
a
2
y
2
b
2
z
2
c
2
x
2
a
2
y
2
b
2
z
2
c
2
This website uses cookies to improve your experience. We'll assume you're ok with this, but you can opt-out if you wish.
Read More
Accept
Reject

3. 6 Hyperboloid of Two Sheets (#4)
+ − = −1
7 Real Quadric Cone (#5)
+ − = 0
8 Imaginary Quadric Cone (#6)
+ + = 0
9 Elliptic Paraboloid (#7)
+ − z = 0
x
2
a
2
y
2
b
2
z
2
c
2
x
2
a
2
y
2
b
2
z
2
c
2
x
2
a
2
y
2
b
2
z
2
c
2
x
2
a
2
y
2
b
2
This website uses cookies to improve your experience. We'll assume you're ok with this, but you can opt-out if you wish.
Read More
Accept
Reject

4. 10 Hyperbolic Paraboloid (#8)
− − z = 0
11 Real Elliptic Cylinder (#9)
+ = 1
12 Imaginary Elliptic Cylinder (#10)
+ = −1
13 Hyperbolic Cylinder (#11)
− = 1
x
2
a
2
y
2
b
2
x
2
a
2
y
2
b
2
x
2
a
2
y
2
b
2
x
2
a
2
y
2
b
2
This website uses cookies to improve your experience. We'll assume you're ok with this, but you can opt-out if you wish.
Read More
Accept
Reject

5. 14 Real Intersecting Planes (#12)
− = 0
15 Imaginary Intersecting Planes (#13)
+ = 0
16 Parabolic Cylinder (#14)
− y = 0
17 Real Parallel Planes (#15)
= 1
18 Imaginary Parallel Planes (#16)
= −1
19 Coincident Planes (#17)
x
2
= 0
20 Equation of a sphere centered at the origin
A sphere is a special case of an ellipsoid when the three semi-axes are the same and equal to the radius of the sphere. The
equation of a sphere of radius R centered at the origin is given by
x
2
+ y
2
+ z
2
= R
2
.
x
2
a
2
y
2
b
2
x
2
a
2
y
2
b
2
x
2
a
2
x
2
a
2
x
2
a
2
This website uses cookies to improve your experience. We'll assume you're ok with this, but you can opt-out if you wish.
Read More
Accept
Reject

6. 21 Equation of a sphere centered at any point
(x − a)
2
+ (y − b)
2
+ (z − c)
2
= R
2
,
where (a, b, c) are the coordinates of the center of the sphere.
22 Diameter form of the equation of a sphere
(x − x1) (x − x2) + (y − y1) (y − y2) + (z − z1) (z − z2) = 0,
where P1 (x1, y1, z1) , P2 (x2, y2, z2) are the endpoints of a diameter.
23 Four points form of the equation of a sphere
∣
∣
∣
∣
∣
∣
∣
∣
x
2
+ y
2
+ z
2
x y z 1
x
2
1
+ y
2
1
+ z
2
1
x1 y1 z1 1
x
2
2
+ y
2
2
+ z
2
2
x2 y2 z2 1
x
2
3
+ y
2
3
+ z
2
3
x3 y3 z3 1
x
2
4
+ y
2
4
+ z
2
4
x4 y4 z4 1
∣
∣
∣
∣
∣
∣
∣
∣
= 0.
The points P1 (x1, y1, z1) , P2 (x2, y2, z2) , P3 (x3, y3, z3) , P4 (x4, y4, z4) belong to the given sphere.
24 General equation of a sphere
Ax
2
+ Ay
2
+ Az
2
+ Dx + Ey + F z + M = 0, (A ≠ 0)
The center of the sphere has the coordinates (a, b, c) where
a = − , b = − , c = − .
The radius of the sphere is given by
R = .
Recommended Pages
D
2A
E
2A
F
2A
√D
2
+E
2
+F
2
−4A
2
M
2A
Two-Dimensional Coordinate System
Straight Line in Plane
Circle and Ellipse
Hyperbola and Parabola
Plane
Straight Line in Space
Quadric Surfaces
This website uses cookies to improve your experience. We'll assume you're ok with this, but you can opt-out if you wish.
Read More
Accept
Reject