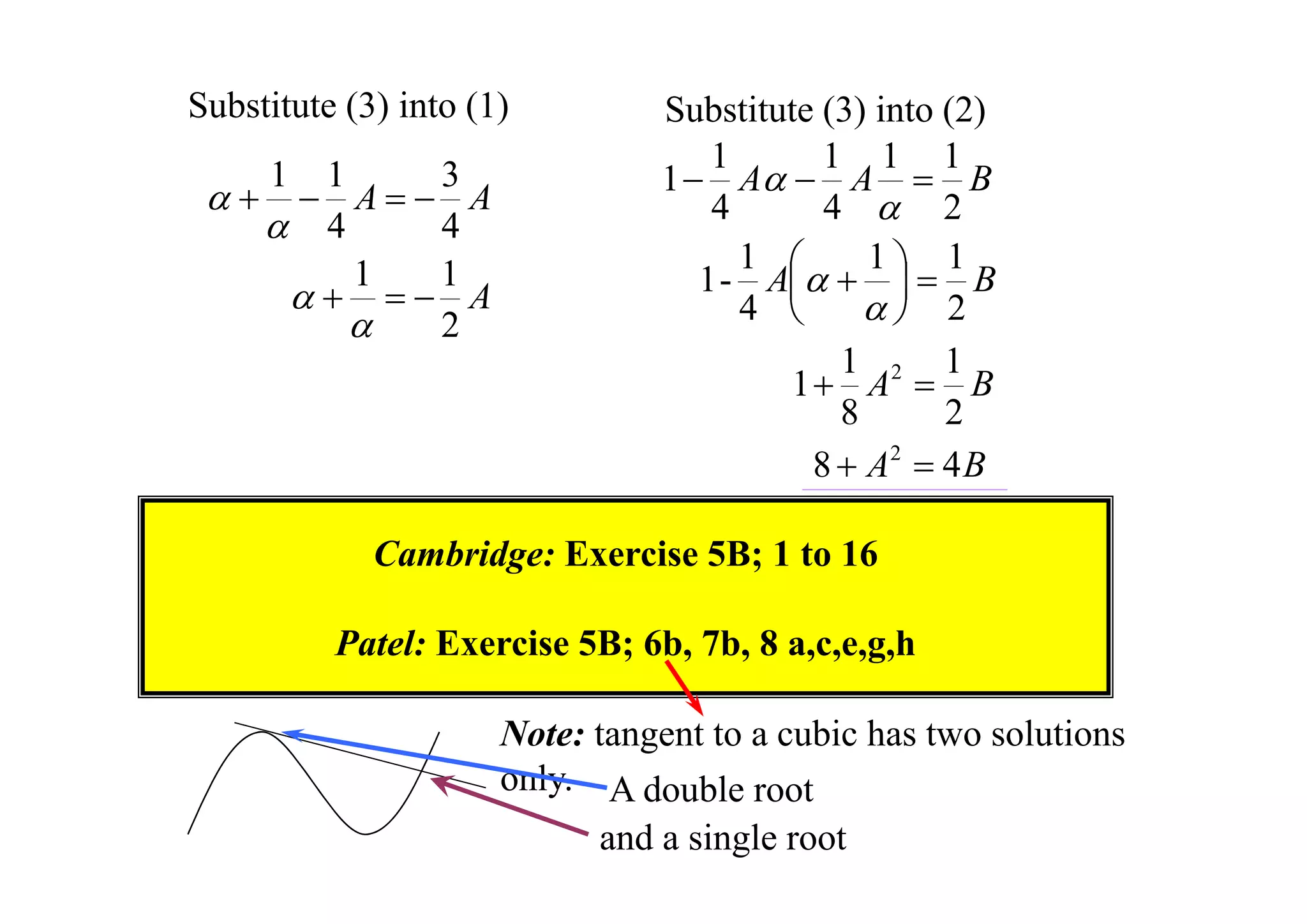
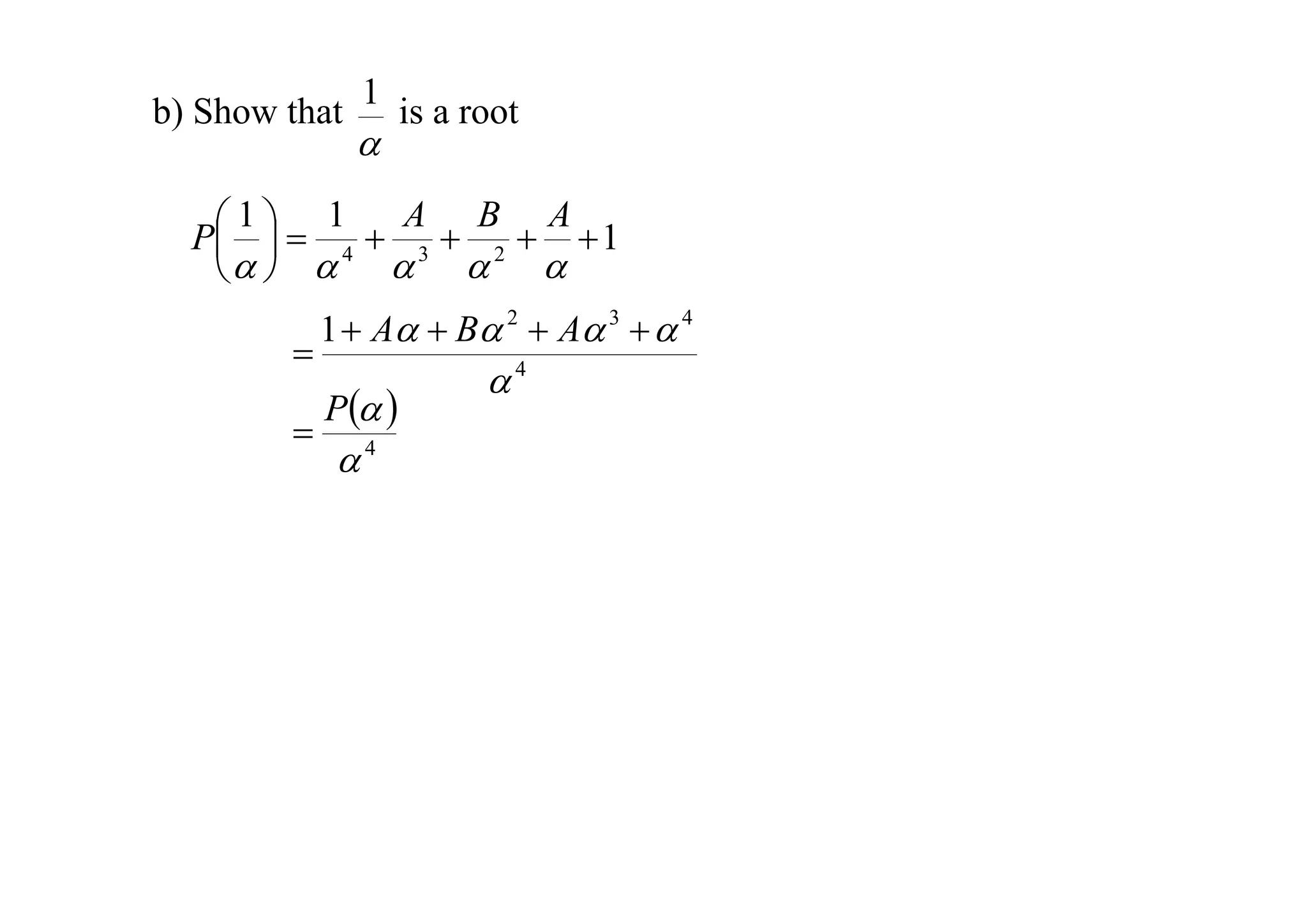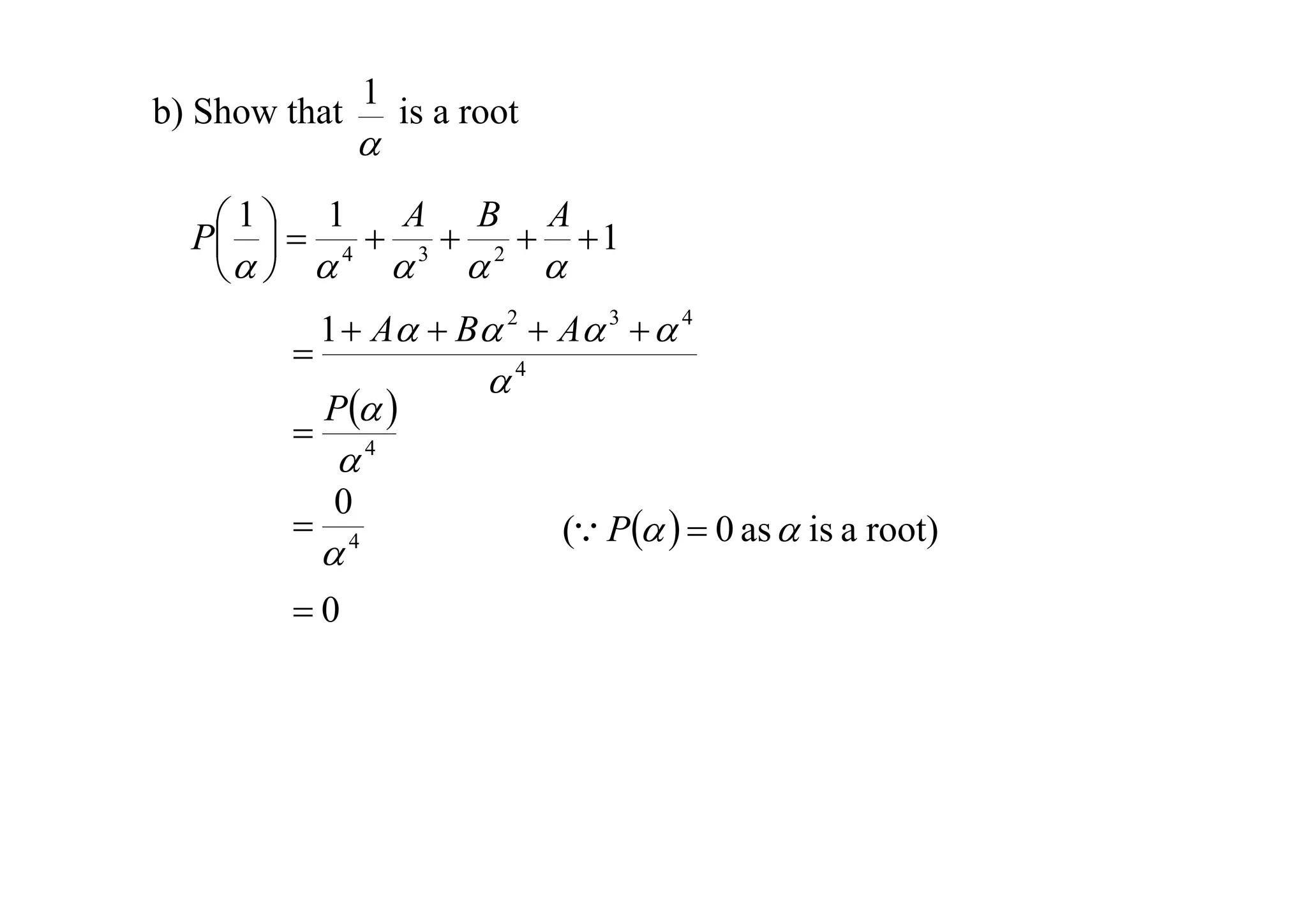P  4 3 2       The document discusses properties of polynomials with multiple roots. It first proves that if a polynomial P(x) has a root x = a of multiplicity m, then the derivative of P(x), P'(x), will have a root x = a of multiplicity m-1. It then provides an example of solving a cubic equation given it has a double root. Finally, it examines a quartic polynomial and shows that its root α cannot be 0, 1, or -1, and that 1/

1. Multiple Roots

2. Multiple Roots
If P(x), has a root, x = a, of multiplicity m,
then P’(x) has a root, x = a, of multiplicity m - 1

3. Multiple Roots
If P(x), has a root, x = a, of multiplicity m,
then P’(x) has a root, x = a, of multiplicity m - 1
Proof:
P x    x  a  Q x 
m
(m > 1, x = a is not a root of Q(x))

4. Multiple Roots
If P(x), has a root, x = a, of multiplicity m,
then P’(x) has a root, x = a, of multiplicity m - 1
Proof:
P x    x  a  Q x 
m
(m > 1, x = a is not a root of Q(x))
P x    x  a  Q x   Q x m x  a 
1
m 1
  x  a   x  a Q x   mQ x 
m
m 1

5. Multiple Roots
If P(x), has a root, x = a, of multiplicity m,
then P’(x) has a root, x = a, of multiplicity m - 1
Proof:
P x    x  a  Q x 
m
(m > 1, x = a is not a root of Q(x))
P x    x  a  Q x   Q x m x  a 
1
m 1
  x  a   x  a Q x   mQ x 
m1
  x  a  R x 
(where x = a is not a root of R(x))
m
m 1

6. Multiple Roots
If P(x), has a root, x = a, of multiplicity m,
then P’(x) has a root, x = a, of multiplicity m - 1
Proof:
P x    x  a  Q x 
m
(m > 1, x = a is not a root of Q(x))
P x    x  a  Q x   Q x m x  a 
1
m 1
  x  a   x  a Q x   mQ x 
m1
  x  a  R x 
(where x = a is not a root of R(x))
m
m 1
 P’(x) has a root, x = a, of multiplicity m - 1

7. e.g. (i) Solve the equation x 3  4 x 2  3 x  18  0 , given that it has a
double root

8. e.g. (i) Solve the equation x 3  4 x 2  3 x  18  0 , given that it has a
double root
P x   x 3  4 x 2  3 x  18
P x   3 x 2  8 x  3

9. e.g. (i) Solve the equation x 3  4 x 2  3 x  18  0 , given that it has a
double root
P x   x 3  4 x 2  3 x  18
P x   3 x 2  8 x  3
 3 x  1 x  3
1
x   or x  3
double root is
3

10. e.g. (i) Solve the equation x 3  4 x 2  3 x  18  0 , given that it has a
double root
P x   x 3  4 x 2  3 x  18
P x   3 x 2  8 x  3
 3 x  1 x  3
1
x   or x  3
double root is
3
NOT POSSIBLE
As (3x + 1) is not a factor

11. e.g. (i) Solve the equation x 3  4 x 2  3 x  18  0 , given that it has a
double root
P x   x 3  4 x 2  3 x  18
P x   3 x 2  8 x  3
 3 x  1 x  3
1
x   or x  3
double root is
3
NOT POSSIBLE
As (3x + 1) is not a factor
x 3  4 x 2  3 x  18  0
 x  32  x  2  0

12. e.g. (i) Solve the equation x 3  4 x 2  3 x  18  0 , given that it has a
double root
P x   x 3  4 x 2  3 x  18
P x   3 x 2  8 x  3
 3 x  1 x  3
1
x   or x  3
double root is
3
NOT POSSIBLE
As (3x + 1) is not a factor
x 3  4 x 2  3 x  18  0
 x  32  x  2  0
x  2 or x  3

13. (ii) (1991)
Let x   be a root of the quartic polynomial;
P x   x 4  Ax 3  Bx 2  Ax  1
where 2  B 2  4 A2
a) show that  cannot be 0, 1 or -1

14. (ii) (1991)
Let x   be a root of the quartic polynomial;
P x   x 4  Ax 3  Bx 2  Ax  1
where 2  B 2  4 A2
a) show that  cannot be 0, 1 or -1
P0   1  0,   0

15. (ii) (1991)
Let x   be a root of the quartic polynomial;
P x   x 4  Ax 3  Bx 2  Ax  1
where 2  B 2  4 A2
a) show that  cannot be 0, 1 or -1
P0   1  0,   0
P1  1  A  B  A  1
 2A  B  2

16. (ii) (1991)
Let x   be a root of the quartic polynomial;
P x   x 4  Ax 3  Bx 2  Ax  1
where 2  B 2  4 A2
a) show that  cannot be 0, 1 or -1
P0   1  0,   0
P1  1  A  B  A  1
 2A  B  2
P 1  1  A  B  A  1
 2 A  B  2

17. (ii) (1991)
Let x   be a root of the quartic polynomial;
P x   x 4  Ax 3  Bx 2  Ax  1
where 2  B 2  4 A2
a) show that  cannot be 0, 1 or -1
P0   1  0,   0
P1  1  A  B  A  1
 2A  B  2
BUT
2  B 2  4 A2
P 1  1  A  B  A  1
 2 A  B  2

18. (ii) (1991)
Let x   be a root of the quartic polynomial;
P x   x 4  Ax 3  Bx 2  Ax  1
where 2  B 2  4 A2
a) show that  cannot be 0, 1 or -1
P0   1  0,   0
P1  1  A  B  A  1
 2A  B  2
BUT
2  B 2  4 A2
2  B  2 A
 2A  B  2  0
P 1  1  A  B  A  1
 2 A  B  2

19. (ii) (1991)
Let x   be a root of the quartic polynomial;
P x   x 4  Ax 3  Bx 2  Ax  1
where 2  B 2  4 A2
a) show that  cannot be 0, 1 or -1
P0   1  0,   0
P1  1  A  B  A  1
 2A  B  2
BUT
2  B 2  4 A2
2  B  2 A
 2A  B  2  0
 P1  0, P 1  0
hence   1
P 1  1  A  B  A  1
 2 A  B  2

20. b) Show that
1

is a root

21. b) Show that
1

is a root
 1   1  A  B  A 1
P 
4
3
2
     

22. b) Show that
1

is a root
 1   1  A  B  A 1
P 
4
3
2
     

1  A  B 2  A 3   4
4

23. b) Show that
1

is a root
 1   1  A  B  A 1
P 
4
3
2
     


1  A  B 2  A 3   4
P 
4
4

24. b) Show that
1

is a root
 1   1  A  B  A 1
P 
4
3
2
     



1  A  B 2  A 3   4
P 
4
4
0
4
0
( P   0 as  is a root)

25. b) Show that
1

is a root
 1   1  A  B  A 1
P 
4
3
2
     



1  A  B 2  A 3   4
P 
4
4
0
4
0
1
 is a root of P x 

( P   0 as  is a root)

26. c) Deduce that if  is a multiple root, then its multiplicity is 2 and
4 B  8  A2

27. c) Deduce that if  is a multiple root, then its multiplicity is 2 and
4 B  8  A2
1
If  is a double root of P x , then so is , which accounts for 4 roots


28. c) Deduce that if  is a multiple root, then its multiplicity is 2 and
4 B  8  A2
1
If  is a double root of P x , then so is , which accounts for 4 roots

However P(x) is a quartic which has a maximum of 4 roots

29. c) Deduce that if  is a multiple root, then its multiplicity is 2 and
4 B  8  A2
1
If  is a double root of P x , then so is , which accounts for 4 roots

However P(x) is a quartic which has a maximum of 4 roots
Thus no roots can have a multiplicity > 2

30. c) Deduce that if  is a multiple root, then its multiplicity is 2 and
4 B  8  A2
1
If  is a double root of P x , then so is , which accounts for 4 roots

However P(x) is a quartic which has a maximum of 4 roots
Thus no roots can have a multiplicity > 2
P x   4 x  3 Ax  2 Bx  A
3
2
let the roots be  ,
1

and 

31. c) Deduce that if  is a multiple root, then its multiplicity is 2 and
4 B  8  A2
1
If  is a double root of P x , then so is , which accounts for 4 roots

However P(x) is a quartic which has a maximum of 4 roots
Thus no roots can have a multiplicity > 2
P x   4 x  3 Ax  2 Bx  A
1
3
   A
4

 1
1     B
 2
1
  A
4
3
2
let the roots be  ,
1

sum of roots  (1)
   (2)
   (3)
and 

32. Substitute (3) into (1)

33. Substitute (3) into (1)

1
1
3
 A A
 4
4
1
1
  A

2

34. Substitute (3) into (1)

1
1
3
 A A
 4
4
1
1
  A

2
Substitute (3) into (2)

35. Substitute (3) into (1)

1
1
3
 A A
 4
4
1
1
  A

2
Substitute (3) into (2)
1
1 1 1
1  A  A  B
4
4  2
1
1
1
1 - A    B


4 
 2
1
1
1  A2  B
8
2
8  A2  4 B

36. Substitute (3) into (1)

1
1
3
 A A
 4
4
1
1
  A

2
Substitute (3) into (2)
1
1 1 1
1  A  A  B
4
4  2
1
1
1
1 - A    B


4 
 2
1
1
1  A2  B
8
2
8  A2  4 B
Cambridge: Exercise 5B; 1 to 16
Patel: Exercise 5B; 6b, 7b, 8 a,c,e,g,h

37. Substitute (3) into (1)

1
1
3
 A A
 4
4
1
1
  A

2
Substitute (3) into (2)
1
1 1 1
1  A  A  B
4
4  2
1
1
1
1 - A    B


4 
 2
1
1
1  A2  B
8
2
8  A2  4 B
Cambridge: Exercise 5B; 1 to 16
Patel: Exercise 5B; 6b, 7b, 8 a,c,e,g,h
Note: tangent to a cubic has two solutions
only. A double root
and a single root