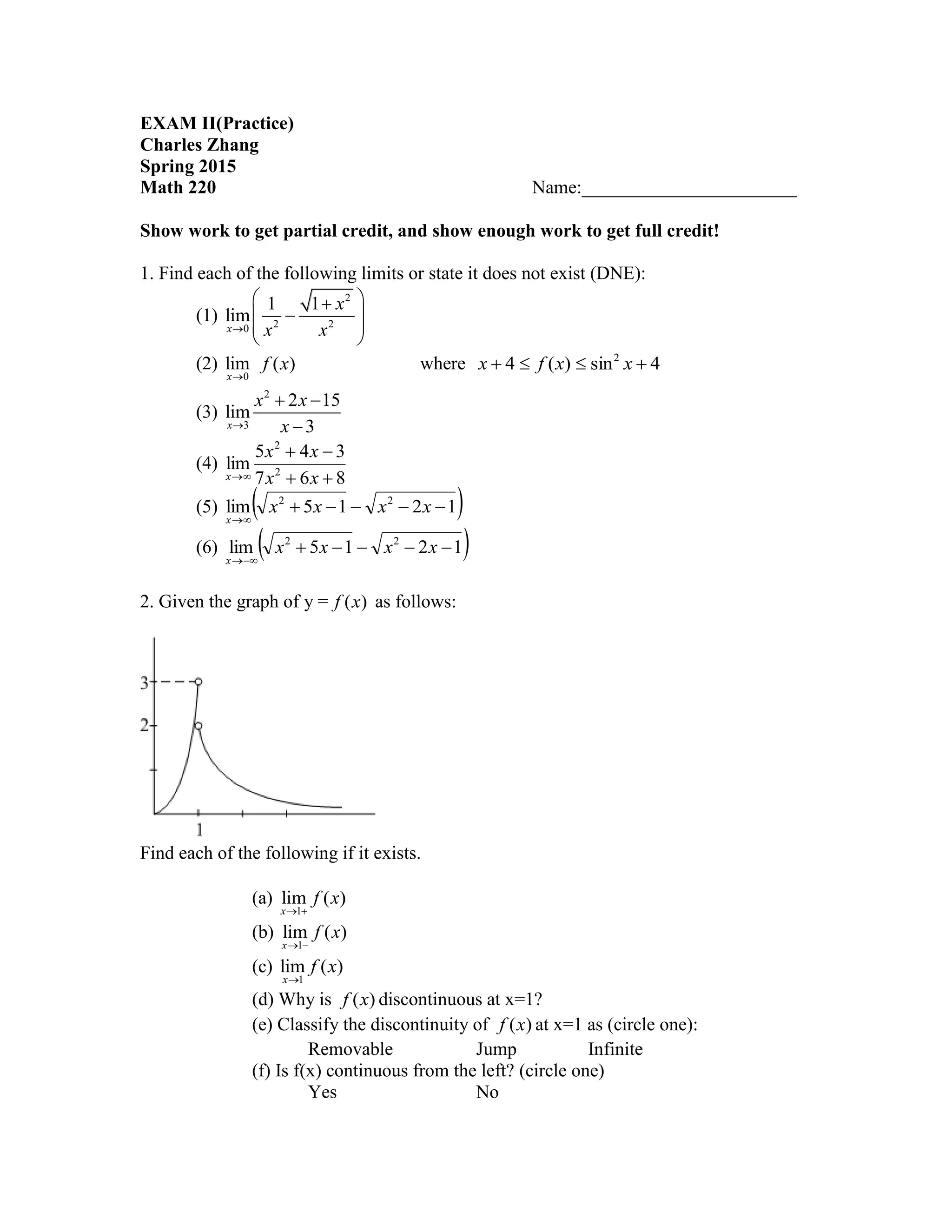
The document is a practice exam for Math 220 that contains 10 problems: 1) Find limits or state if they do not exist. 2) Find limits based on a graph of a function. 3) Find the intervals of continuity for several functions. 4) Solve limit problems related to epsilon-delta definitions of limits. 5) Use the Intermediate Value Theorem to show an equation has a solution. 6) Evaluate a limit involving a constant. 7) Find function values to make a piecewise function continuous. 8) Find a limit as a variable approaches 2π. 9) Find derivatives of several functions by definition. 10) Find a value to make a piecewise function

1. EXAM II(Practice)
Charles Zhang
Spring 2015
Math 220 Name:_______________________
Show work to get partial credit, and show enough work to get full credit!
1. Find each of the following limits or state it does not exist (DNE):
(1)
2
2 20
1 1
lim
x
x
x x
 
 
 
 
(2)
0
lim
x
( )f x where 4sin)(4 2
 xxfx
(3)
2
3
2 15
lim
3x
x x
x
 

(4)
867
345
lim 2
2


 xx
xx
x
(5)  1215lim 22


xxxx
x
(6)  1215lim 22


xxxx
x
2. Given the graph of y = ( )f x as follows:
Find each of the following if it exists.
(a)
1
lim ( )
x
f x
 
(b)
1
lim ( )
x
f x
 
(c)
1
lim ( )
x
f x

(d) Why is ( )f x discontinuous at x=1?
(e) Classify the discontinuity of ( )f x at x=1 as (circle one):
Removable Jump Infinite
(f) Is f(x) continuous from the left? (circle one)
Yes No

2. (g) Is f(x) continuous from the right? (circle one)
Yes No
3. Find the interval over which each of the following function is continuous:
(a) ln( 2)y x 
(b) 2
sin( 2)y x 
(c)
1
2
y
x


4. (a) How close to 3 do we have to take x so that 7x - 6 is within a distance of 0.001
from 15? The equivalent problem is: find  such that
|(7x - 6) - 15|< 0.001 whenever |x - 3|<  .
(b) What is the related limit? (Circle one)
(1)
15
lim
x
(7x - 6) = 3
(2)
3
lim
x
(7x - 6) = 15
(3)
3
lim
x
(7x - 6) does not exist
(4)
3
lim
x
(7x - 6) = .001
5. Use The Intermediate Value Theorem to show that the equation cos sin 0x x x  has
a solution in the interval
.
 2 , 3 
..
6. Evaluate the limit in terms of the constant involved:
1 1
lim , 0
h a
a h a
h a



7. Find the values of , ,a b c which make the function continuous:













xifc
xbifx
bxifxx
xifa
xf
4
43
0)8(
4
1
0
)(
8. Find the limit:








 2
sinlim
0 x
x
x


3. 9. Find each of the following derivatives by definition:
(a) )2(f  for
3
2
)(


x
xf
(b) )(ag for 1)(  ttg
(c) )(xh for 32)( 2
 xxxh
10. Find the value of a so that the following function will be continuous every where:










5
5
5
152
)(
2
xifa
xif
x
xx
xf