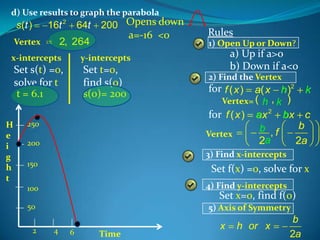
1) The function s(t) = 16t^2 - 64t + 200 models the height of a baseball thrown vertically upward from a 200-foot building. 2) The ball reaches its maximum height of 216 feet after 2 seconds. 3) It takes 4 seconds for the ball to hit the ground again. 4) The y-intercept s(0) = 200 feet represents the initial height from which the ball was thrown.

1. The Characteristics of Parabolas – Points of Interest
Opens Up
x-int
Axis of Sym
x=1
Min (-1,-3)
Axis of Sym
x=1
a) Up if a>o
b) Down if a<o
Quadratic equations in
in this form:
f ( x ) ax 2 bx c
y-int 2) Vertex
Vertex
Max (-1,5)
a) Minimum if a>o
b) Maximum if a<o
3) x-intercepts
a) Where f(x) =0
4) y-intercepts
y-int
Opens
Down
1) Open Up or Down?
a) Where x=0
5) Axis of Symmetry
x-int
a) The x-value at the
vertex
f (x)
a( x
h )2
k

2. Solving Quadratic
equations in this form:
ax
2
bx
c
0, a
1) Factoring
2) Square Root Property
2
If u
d,
then u
d
3) The Quadratic Formula
x
b
b
2
2a
4ac
0
Which
one to
use?

3. Ch 11.2 #2,6,9,18
x2
#2
8 x 15
0
a 1b
,
x
x
x
Quadratic equations in
this form:
ax 2 bx c 0, a 0
8, c 15
( 8)
2
8
1) Factoring
4 • 1 • 15
2) Square Root Property
If u 2
2 1
8
-8
then u
64 60
2
4
x
4 1
3 or
d
3) The Quadratic
Formula
2
8 2
x
2
x
4 1
x -5,-3
d,
x
4 1
5
b
b
2
2a
4ac

4. Ch 11.2 #2,6,9,18
#6
x2
5 x 10
a 1b
,
( 5)
x
5
10
2
4 • 1 • -10
1) Factoring
2) Square Root Property
If u 2
2 1
5
x
x
5,c
0
Quadratic equations in
this form:
ax 2 bx c 0, a 0
-5
25 40
2
d,
then u
3) The Quadratic
Formula
65
2
d
x
b
b
2
2a
4ac

5. Ch 11.2 #2,6,9,18
# 9 6x
6x
a
2
2x 1
2x 1 0
6, b
( -2)
x
x
2
2, c
-2
2
4
12
24
1) Factoring
2) Square Root Property
If u 2
1
4 • 6 • -1
2 6
2
Quadratic equations in
this form:
ax 2 bx c 0, a 0
2
28
12
2 2 7
12
d,
then u
d
3) The Quadratic
Formula
x
2(1
7)
2 6
b
b
2
2a
1
7
6
4ac

6. Ch 11.2 #2,6,9,18
Quadratic equations in
this form:
ax 2 bx c 0, a 0
#18 2x( x 4) 3x 3
2x 2 8 x 3 x 3
2x
a
x
x
x
2
5x 3
2, b
(5 )
0
5, c
5
2
1) Factoring
2) Square Root Property
If u 2
3
then u
4• 2 • 3
6
4
25 24
4
3
or x
2
5
5 1
4
1
4
4
4
1
d
3) The Quadratic
Formula
2 2
5
d,
x
x
3
,
2
b
b
2
2a
1
4ac

7. Ch 11.2 #42,43,46
# 42
4x-1
2
15
4 x -1
4x
x
15
1
Which one
to use?
Quadratic equations in
this form:
ax 2 bx c 0, a 0
1) Factoring
2) Square Root Property
If u 2
15
1
15
4
d,
then u
d
3) The Quadratic
Formula
x
b
b
2
2a
4ac

8. Ch 11.2 #42,43,46
1
x
# 43
3x x+2
3 x
2
1
1
3 LCD 3 x x
x 2
1
x
1
x 2
3x
3x 6 3x
x
2
1
3
4x 6
x x
x
2
0
Quadratic equations in
this form:
ax 2 bx c 0, a 0
2
1) Factoring
2) Square Root Property
If u 2
d,
then u
2
2x
d
3) The Quadratic
Formula
x
b
b
2
2a
4ac

9. Ch 11.2 #42,43,46
x
2
4x 6
a 1b
,
Which one
to use?
0
4, c
Quadratic equations in
this form:
ax 2 bx c 0, a 0
1) Factoring
2) Square Root Property
6
If u 2
# 46
7x x-2
7x2 14x
3 2 x
then u
4
3 2x 8
7x
12x 5
0 Which one
to use?
d
3) The Quadratic
Formula
x
2
d,
b
b
2
2a
4ac

10. Writing an equation when
solutions are given
Ch 11.2 #48,54
# 48
x
2,6
2 or x
Quadratic equations in
this form:
ax 2 bx c 0, a 0
1) Factoring
2) Square Root Property
6
If u 2
Work backwards
x
2
x
x
2
0 or x - 6
2 x 6
4x 12
0
0
0
d,
then u
d
3) The Quadratic
Formula
x
b
b
2
2a
4ac

11. Writing an equation when
solutions are given
Ch 11.2 #48,54
# 54
x
3, 3
3
0 or x
3
0
Quadratic equations in
this form:
ax 2 bx c 0, a 0
1) Factoring
2) Square Root Property
If u 2
Work backwards
x
3
x
3 =0
then u
x
3
0
d
3) The Quadratic
Formula
x
2
d,
b
b
2
2a
4ac

12. The Shape of the Graph of a
Quadratic Equation:
a Parabola
Quadratic equations in
in this form:
f ( x ) ax 2 bx c
f (x)
a( x
h )2
k

13. The Characteristics of Parabolas – Points of Interest
Opens Up
x-int
Axis of Sym
x= -1
Min (-1,-3)
Axis of Sym
x= -1
a) Up if a>o
b) Down if a<o
Quadratic equations in
in this form:
f ( x ) ax 2 bx c
y-int 2) Vertex
Vertex
Max (-1,5)
a) Minimum if a>o
b) Maximum if a<o
3) x-intercepts
a) Where f(x) =0
4) y-intercepts
y-int
Opens
Down
1) Open Up or Down?
a) Where x=0
5) Axis of Symmetry
x-int
a) The x-value at the
vertex
f (x)
a( x
h )2
k

14. Graphing Parabolas in form
Ch 11.3 #10,11,14,16 Find the Vertex
#10
f ( x ) -3 x - 2
h 2
vertex
k
2
12
(2,12)
12
ax 2
bx
c
a( x
Rules
h )2
k
f (x)
f (x)
1) Open Up or Down?
a) Up if a>o
b) Down if a<o
2) Find the Vertex
a( x h )2 k
Vertex= ( h , k )
for f ( x ) a 2 b
ax bx c
b
b ,f
Vertex
2a
2a
for f ( x )
3) Find x-intercepts
Set f(x) =0, solve for x
4) Find y-intercepts
Set x=0, find f(0)
5) Axis of Symmetry
x
h or x
b
2a

15. Graphing Parabolas in form
Ch 11.3 #10,11,14,16 Find the Vertex
#11 f ( x ) -2 x 1
2
1
f ( x ) -2 x ( 1)
ax 2
bx
c
a( x
Rules
h )2
k
f (x)
f (x)
1) Open Up or Down?
a) Up if a>o
b) Down if a<o
5
2
h
1 k 5
vertex
(-1,5)
5
2) Find the Vertex
for f ( x )
a( x h )2 k
Vertex= ( h , k )
for f ( x ) a 2 b
ax bx c
b
b ,f
Vertex
2a
2a
3) Find x-intercepts
Set f(x) =0, solve for x
4) Find y-intercepts
Set x=0, find f(0)
5) Axis of Symmetry
x
h or x
b
2a

16. Ch 11.3 #10,11,14,16 Find the Vertex
#14
f ( x ) 3 x 2 12 x 1
12
a 3 b
( 12)
2(3)
f ( 2)
Vertex
3 2
12
6
2
1) Open Up or Down?
a) Up if a>o
b) Down if a<o
2
12 2
b
2 ,
2a
Rules
11
f ( 2)
1 12 24 1
11
2) Find the Vertex
for f ( x )
k
for f ( x )
a 2 b
ax bx c
b
b ,f
2a
2a
a( x h )2
Vertex= ( h , k )
Vertex
3) Find x-intercepts
Set f(x) =0, solve for x
4) Find y-intercepts
Set x=0, find f(0)
5) Axis of Symmetry
x
h or x
b
2a

17. Ch 11.3 #10,11,14,16 Find the Vertex
#16
2x 2 8x 1
2 b 8
f (x)
a
(8 )
2( 2)
f ( 2)
Vertex
8
4
2 2
2
b
2 ,
2a
Rules
1) Open Up or Down?
a) Up if a>o
b) Down if a<o
2
8 2
f (7 )
2
1
8 16 1 7
2) Find the Vertex
for f ( x )
k
for f ( x )
a 2 b
ax bx c
b
b ,f
2a
2a
a( x h )2
Vertex= ( h , k )
Vertex
3) Find x-intercepts
Set f(x) =0, solve for x
4) Find y-intercepts
Set x=0, find f(0)
5) Axis of Symmetry
x
h or x
b
2a

18. Ch 11.3 #18,34 Graph Opens
2
#18
f x
x 1
2 up
a=1 >0
h 1 k
2
vertex
x-intercepts
y-intercepts
(1
2,0) (1
2,0)
f (0 )
1) Open Up or Down?
a) Up if a>o
b) Down if a<o
(1, 2)
2
x 1
2 0
2
x 1
2
x 1 ± 2
x 1± 2
Rules
2
0 1
2
2
1
2
1 2
1
(0, 1)
2) Find the Vertex
for f ( x )
a( x h )2 k
Vertex= ( h , k )
for f ( x ) a 2 b
ax bx c
b
b ,f
Vertex
2a
2a
3) Find x-intercepts
Set f(x) =0, solve for x
4) Find y-intercepts
Set x=0, find f(0)
5) Axis of Symmetry
x
x
h or x
1
b
2a

19. # 34
6 4 x x 2 Opens
x 2 4 x 6 up >0
a=1
4
a 1 b
f x
f x
Vertex
4
b
2(1)
2(a )
f ( 2)
Vertex
4
2
2
2
4 2
b
2a
2 ,
Rules
1) Open Up or Down?
a) Up if a>o
b) Down if a<o
2) Find the Vertex
2
for f ( x )
6
f (2 )
4 8 6 2
a( x h )2 k
Vertex= ( h , k )
for f ( x ) a 2 b
ax bx c
b
b ,f
Vertex
2a
2a
3) Find x-intercepts
Set f(x) =0, solve for x
4) Find y-intercepts
Set x=0, find f(0)
5) Axis of Symmetry
x
h or x
b
2a

20. 6 4 x x 2 Opens
x 2 4 x 6 up
a=1 >0
Vertex = (2,2)
# 34
f x
f x
x-intercepts
x
2
4x
6
y-intercepts
0
Use Quad. Form.
OR
Look at the graph
so far....
No x intercepts
f (0)
0
2
6
(0,6)
4(0) 6
Rules
1) Open Up or Down?
a) Up if a>o
b) Down if a<o
2) Find the Vertex
for f ( x )
a( x h )2 k
Vertex= ( h , k )
for f ( x ) a 2 b
ax bx c
b
b ,f
Vertex
2a
2a
3) Find x-intercepts
Set f(x) =0, solve for x
4) Find y-intercepts
Set x=0, find f(0)
5) Axis of Symmetry
x
x
h or x
2
b
2a

21. Finding Minimum and Maximum
Ch 11.3 #60
Definition
A person standing close to the edge
on the top of a 200-foot building
throws a baseball vertically upward.
The quadratic function
s (t )
16t 2
64t
200
If parabola opens………
a) Up (a>o)
Vertex = Min
b) Down (a<o)
Vertex = Max
models the ball’s height above the
ground, s(t), in feet, t seconds after it Rules
1) Determine what needs to
was thrown.
be maximized or
a) After how many seconds does the ball
reach max height? What is the max height?
b) How many seconds does it take until the
ball finally hits the ground?
c) Find s(0) and describe what it means
d) Use results to graph the parabola
minimized
2) Express quantity as
function
3) Rewrite in form:
f (x)
ax 2
bx c
4) Calculate Max or
Min by finding the
vertex

22. Max point…
Vertex = (t, s(t))
s (t )
16t 2
a
is the Vertex
64t
200
16 b
64
Feet from ground
at max
Seconds it took to
reach max
a) After how many seconds
does the ball reach max
height? What is the max
height?
Find the vertex to find max
time, t, and max height, s(t)
200 ft
Vertex
Vertex
b
64 , s
16)
2( a
2 sec ,
b
2a
s(2)

23. Max point…
MAX at (2 sec, s(t))feet)
Vertex = (t, 264
s (t )
16t 2
a
is the Vertex
64t
200
16 b
64
a) After how many seconds
does the ball reach max
height? What is the max
height?
Vertex
s( 2 )
s ( 2)
200 ft
s ( 2)
2 sec , 264 (2)
s feet
16( 2 )2
64( 2 ) 200
64 128 200
264 feet
It took 2 seconds to reach a
maximum height of 264 feet

24. Max point…
MAX at (2 sec, 264 feet)
16t 2
s (t )
a
is the Vertex
64t
200
16 b
64
b) How many seconds does it
take until the ball finally hits
the ground?
s(t)
16t 2
Factor out -2
8t 2
0
64t
200
32t 100
0
0
Use Quadratic Formula to slove
200 ft
What is the height , s(t) , when
the ball hits the ground?
s(t)
0

25. Max point…
MAX at (2 sec, 264 feet)
s (t )
16t 2
a
is the Vertex
64t
200
16 b
64
b) How many seconds does it
take until the ball finally hits
the ground?
8t 2 32t 100 0
32 c
a 8 b
t
( 32) ±
t
32
32
2
100
4(8)( 100)
2(8)
1024 3200
16
200 ft
What is the height , s(t) , when
the ball hits the ground?
s(t)
0

26. Max point…
MAX at (2 sec, 264 feet)
s (t )
16t 2
a
is the Vertex
64t
200
16 b
64
b) How many seconds does it
take until the ball finally hits
the ground?
8t 2 32t 100 0
32 c
a 8 b
t
( 32) ±
t
200 ft
32
2
4(8)( 100)
2(8)
32
1024 3200
16
32 64.99
16
6.1 seconds
100

27. Max point…
MAX at (2 sec, 264 feet)
s (t )
16t 2
a
is the Vertex
64t
200
16 b
64
c) Find s(0) and describe what
it means
t =0 means zero seconds
Where is the baseball at zero
seconds?
s (0 )
s (0 )
200 ft
16(0)2
64(0) 200
200 feet
The ball is in the thrower’s
hand at the top of the
building, 200 feet up.

28. d) Use results to graph the parabola
s (t )
Vertex
16t 2
64t
200 Opens down
2, 264
a=-16 <0
x-intercepts
Set t=0,
find s(0)
s(o)= 200
1) Open Up or Down?
a) Up if a>o
b) Down if a<o
y-intercepts
Set s(t) =0,
solve for t
t = 6.1
Rules
2) Find the Vertex
for f ( x )
a( x h )2 k
Vertex= ( h , k )
for f ( x ) a 2 b
ax bx c
b
b ,f
Vertex
2a
2a
3) Find x-intercepts
Set f(x) =0, solve for x
4) Find y-intercepts
Set x=0, find f(0)
5) Axis of Symmetry
x
h or x
b
2a

29. d) Use results to graph the parabola
16t 2
s (t )
64t
200 Opens down
a=-16 <0
2, 264
Vertex
x-intercepts
Set t=0,
find s(0)
s(o)= 200
1) Open Up or Down?
a) Up if a>o
b) Down if a<o
y-intercepts
Set s(t) =0,
solve for t
t = 6.1
Rules
H
e
i
g
h
t
250
200
2) Find the Vertex
for f ( x )
a( x h )2 k
Vertex= ( h , k )
for f ( x ) a 2 b
ax bx c
b
b ,f
Vertex
2a
2a
3) Find x-intercepts
150
Set f(x) =0, solve for x
4) Find y-intercepts
100
Set x=0, find f(0)
50
2
5) Axis of Symmetry
4
6
Time
x
h or x
b
2a

30. •Tonight’s Lecture portion Ch 11.2 & 11.3: •DONE
•5 points for Attendance given at:
•8:30 PM
•Homework Assignments due by 8:30PM:•Ch 11.2 & 11.3
•Tonight’s Assignments already done? :
•Turn them in BEFORE you leave
•Receive 5 points for attendance
•You may leave anytime AFTER the LECTURE portion
•Arriving late (after 6:45 pm) AND THEN leaving early:
•Receive ZERO points for attendance

31. The Characteristics of Parabolas – Points of Interest
Opens Up
x-int
Axis of Sym
x=1
Min (-1,-3)
Axis of Sym
x=1
a) Up if a>o
b) Down if a<o
Quadratic equations in
in this form:
f ( x ) ax 2 bx c
y-int 2) Vertex
Vertex
Max (-1,5)
a) Minimum if a>o
b) Maximum if a<o
3) x-intercepts
a) Where f(x) =0
4) y-intercepts
y-int
Opens
Down
1) Open Up or Down?
a) Where x=0
5) Axis of Symmetry
x-int
a) The x-value at the
vertex
f (x)
a( x
h )2
k