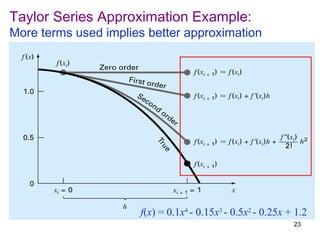
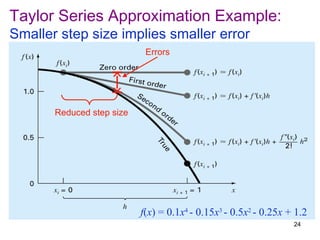
Let's analyze the remainder term R6 using the geometry series method: |tj+1| = (j+1)π-2 ≤ π-2 = k|tj| for all j ≥ 6 (where 0 < k = π-2 < 1) Then, |R6| ≤ t7(1 + k + k2 + k3 + ...) = t7/(1-k) = 7π-2/(1-π-2) So the estimated upper bound of the truncation error |R6| is 7π-2/(1-π-2)

1. Part 3
Truncation Errors
1

2. Key Concepts
• Truncation errors
• Taylor's Series
– To approximate functions
– To estimate truncation errors
• Estimating truncation errors using other
methods
– Alternating Series, Geometry series,
Integration
2

3. Introduction
How do we calculate
sin( x), cos( x), e x , x y , x , log( x), ...
on a computer using only +, -, x, ÷?
One possible way is via summation of infinite
series. e.g.,
x2 x3 xn x n +1
ex = 1 + x + + + ... + + + ...
2! 3! n! ( n + 1)!
3

4. Introduction
x2 x3 xn x n +1
e =1+ x +
x
+ + ... + + + ...
2! 3! n! ( n + 1)!
• How to derive the series for a given function?
• How many terms should we add?
or
• How good is our approximation if we only sum
up the first N terms?
4

5. A general form of approximation is in
terms of Taylor Series.
5

6. Taylor's Theorem
Taylor's Theorem: If the function f and its first n+1
derivatives are continuous on an interval containing a
and x, then the value of the function at x is given by
f " (a) f ( 3) ( a )
f ( x) = f (a) + f ' (a)( x − a ) + ( x − a) 2 + ( x − a )3 + ...
2! 3!
f ( n ) (a)
+ ( x − a ) n + Rn
n!
where the remainder Rn is defined as
x ( x − t ) n ( n +1)
Rn = ∫a n!
f (t )dt (the integral form)
6

7. Derivative or Lagrange Form of the remainder
The remainder Rn can also be expressed as
( n +1)
f (c ) (the Lagrange form)
Rn = ( x − a ) n +1
(n + 1)!
for some c between a and x
The Lagrange form of the remainder makes
analysis of truncation errors easier.
7

8. Taylor Series
f " (a ) f ( 3) ( a )
f ( x ) = f ( a ) + f ' ( a )( x − a ) + ( x − a)2 + ( x − a ) 3 + ...
2! 3!
f ( n ) (a )
+ ( x − a ) n + Rn
n!
• Taylor series provides a mean to approximate any
smooth function as a polynomial.
• Taylor series provides a mean to predict a function
value at one point x in terms of the function and its
derivatives at another point a.
• We call the series "Taylor series of f at a" or "Taylor
series of f about a".
8

9. Example – Taylor Series of ex at 0
f ( x) = e x => f ' ( x) = e x => f " ( x) = e x => f ( k ) ( x) = e x for any k ≥ 0
Thus f ( k ) (0) = 1 for any k ≥ 0.
With a = 0, the Taylor series of f at 0 becomes
f " ( 0) f ( n ) (0)
f (0) + f ' (0)( x − 0) + ( x − 0) 2 + ... + ( x − 0) n + ...
2! n!
x 2 x3 xn
= 1 + x + + + ... + + ...
2! 3! n!
Note:
Taylor series of a function f at 0 is also known as the
Maclaurin series of f.
9

10. Exercise – Taylor Series of cos(x) at 0
f ( x ) = cos( x ) => f (0) = 1 f ' ( x ) = − sin( x ) => f ' (0) = 0
f " ( x ) = − cos( x ) => f " (0) = −1 f ( 3) ( x ) = sin( x ) => f ( 3) (0) = 0
f ( 4 ) ( x ) = cos( x ) => f ( 4 ) (0) = 1 f ( 5) ( x ) = − sin( x ) => f ( 5) (0) = 0

With a = 0, the Taylor series of f at 0 becomes
f " ( 0) f ( n ) ( 0)
f (0) + f ' (0)( x − 0) + ( x − 0) + ... +
2
( x − 0) n + ...
2! n!
x2 x4 x6
=1+ 0 − +0 + +0 − + ...
2! 4! 6!
∞ 2n
n x
= ∑( −1)
n =0 ( 2n )!
10

11. Question
x2 x3 xn x n +1
ex = 1 + x + + + ... + + + ...
2! 3! n! ( n + 1)!
What will happen if we sum up only the first n+1
terms?
11

12. Truncation Errors
Truncation errors are the errors that result from
using an approximation in place of an exact
mathematical procedure.
Approximation Truncation Errors
x2 x3 xn x n +1
ex = 1 + x + + + ... + + + ...
2! 3! n! ( n + 1)!
Exact mathematical formulation
12

13. How good is our approximation?
x2 x3 xn x n +1
ex = 1 + x + + + ... + + + ...
2! 3! n! ( n + 1)!
How big is the truncation error if we only sum up
the first n+1 terms?
To answer the question, we can analyze the
remainder term of the Taylor series expansion.
f " (a) f ( 3) ( a )
f ( x) = f (a) + f ' (a)( x − a) + ( x − a) 2 + ( x − a)3 + ...
2! 3!
f ( n ) (a)
+ ( x − a) n + Rn
n!
13

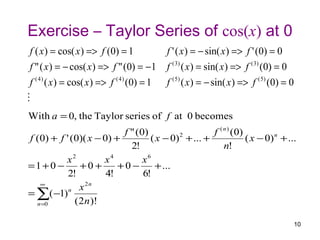
14. Analyzing the remainder term of the
Taylor series expansion of f(x)=ex at 0
The remainder Rn in the Lagrange form is
( n +1)
f (c )
Rn = ( x − a ) n +1
(n + 1)! for some c between a and x
For f(x) = ex and a = 0, we have f(n+1)(x) = ex. Thus
ec
Rn = x n +1 for some c in [0 , x]
(n + 1)!
x
e We can estimate the largest possible
≤ x n +1 truncation error through analyzing Rn.
(n + 1)!
14

15. Example
Estimate the truncation error if we calculate e as
1 1 1 1
e = 1 + + + + ... +
1! 2! 3! 7!
This is the Maclaurin series of f(x)=ex with x = 1 and
n = 7. Thus the bound of the truncation error is
ex 7 +1 e1 8 e −4
R7 ≤ x = (1) = ≈ 0.6742 × 10
(7 + 1)! 8! 8!
The actual truncation error is about 0.2786 x 10-4.
15

16. Observation
For the same problem, with n = 8, the bound of the truncation
error is e
R8 ≤ ≈ 0.7491 × 10−5
9!
With n = 10, the bound of the truncation error is
e
R10 ≤ ≈ 0.6810 × 10−7
11!
More terms used implies better approximation.
16

17. Example (Backward Analysis)
This is the Maclaurin series expansion for ex
x2 x3 xn
e x = 1 + x + + + ... + + ...
2! 3! n!
If we want to approximate e0.01 with an error
less than 10-12, at least how many terms are
needed?
17

18. With x = 0.01, 0 ≤ c ≤ 0.01, f ( x ) = e x => f ( n +1) ( x ) = e x
ec n +1 e0.01 n +1 1.1
Rn = x ≤ (0.01) < (0.01) n +1
( n + 1)! ( n + 1)! ( n + 1)!
Note:1.1100 is about 13781 > e
To find the smallest n such that Rn < 10-12, we can find
the smallest n that satisfies
1.1 n +1 −12 With the help of a computer:
(0.01) < 10
( n + 1)! n=0 Rn=1.100000e-02
n=1 Rn=5.500000e-05
n=2 Rn=1.833333e-07
n=3 Rn=4.583333e-10
So we need at least 5 terms n=4 Rn=9.166667e-13
18

19. Same problem with larger step size
With x = 0.5, 0 ≤ c ≤ 0.5, f ( x ) = e x => f ( n +1) ( x ) = e x
ec n +1 e0.5 n +1 1.7
Rn = x ≤ (0.5) < (0.5) n +1
( n + 1)! ( n + 1)! ( n + 1)!
Note:1.72 is 2.89 > e
With the help of a computer: n=5 Rn=3.689236e-05
n=0 Rn=8.500000e-01 n=6 Rn=2.635169e-06
n=1 Rn=2.125000e-01 n=7 Rn=1.646980e-07
n=2 Rn=3.541667e-02 n=8 Rn=9.149891e-09
n=3 Rn=4.427083e-03 n=9 Rn=4.574946e-10
n=4 Rn=4.427083e-04 n=10 Rn=2.079521e-11
n=11 Rn=8.664670e-13
So we need at least 12 terms
19

20. To approximate e10.5 with an error less than 10-12,
we will need at least 55 terms. (Not very efficient)
How can we speed up the calculation?
20

21. Exercise
If we want to approximate e10.5 with an error less
than 10-12 using the Taylor series for f(x)=ex at 10,
at least how many terms are needed?
The Taylor series expansion of f ( x ) at 10 is
f ' (10) f " (10) f ( n ) (10)
f ( x ) = f (10) + ( x − 10) + ( x − 10) + ... +
2
( x − 10) n + Rn
1! 2! n!
( x − 10) 2 ( x − 10) n
= e (1 + ( x − 10) +
10
+ ... + ) + Rn
2! n!
f ( n +1) ( c )
Rn = ( x − 10) n +1 for some c between 10 and x
( n + 1)!
The smallest n that satisfy Rn < 10-12 is n = 18. So we need
at least 19 terms.
21

22. Observation
• A Taylor series converges rapidly near the
point of expansion and slowly (or not at
all) at more remote points.
22

23. Taylor Series Approximation Example:
More terms used implies better approximation
f(x) = 0.1x4 - 0.15x3 - 0.5x2 - 0.25x + 1.2
23

24. Taylor Series Approximation Example:
Smaller step size implies smaller error
Errors
Reduced step size
f(x) = 0.1x4 - 0.15x3 - 0.5x2 - 0.25x + 1.2
24

25. Taylor Series (Another Form)
If we let h = x – a, we can rewrite the Taylor series
and the remainder as
(n)
f " (a) 2 f (a) n
f ( x) = f (a) + f ' (a)h + h + ... + h + Rn
2! n!
f ( n +1) (c) n +1 When h is small, hn+1 is much
Rn = h
(n + 1)! smaller.
h is called the step size.
h can be +ve or –ve.
25

26. The Remainder of the Taylor Series Expansion
f ( n +1) ( c) n +1 n +1
Rn = h = O (h )
( n + 1)!
Summary
To reduce truncation errors, we can reduce h or/and
increase n.
If we reduce h, the error will get smaller quicker (with less n).
This relationship has no implication on the magnitude of the
errors because the constant term can be huge! It only give
us an estimation on how much the truncation error would
reduce when we reduce h or increase n.
26

27. Other methods for estimating
truncation errors of a series
S = t0 + t1 + t 2 + t3 + ... + t n + t n +1 + t n + 2 + t n +3 + ...
       
Sn Rn
1. By Geometry Series
2. By Integration
3. Alternating Convergent Series Theorem
Note: Some Taylor series expansions may exhibit certain
characteristics which would allow us to use different methods
to approximate the truncation errors.
27

28. Estimation of Truncation Errors
By Geometry Series
If |tj+1| ≤ k|tj| where 0 ≤ k < 1 for all j ≥ n, then
Rn = tn +1 + tn +2 + tn +3 +...
≤ tn +1 + k tn +1 + k 2 tn +1 +...
= tn +1 (1 + k + k 2 + k 3 +...)
tn +1
=
1 −k
k tn
Rn ≤
1− k
28

29. Example (Estimation of Truncation Errors by Geometry Series)
What is |R6| for the following series expansion?
S =1 +π −2 + 2π −4 + 3π −6 +... + jπ −2 j +...
tj = jπ −2 j
Solution: t j +1 j +1π−2 j −2 1
= = 1 + π−2
Is there a k (0 ≤ k < 1) s.t. tj jπ−2 j j
|tj+1| ≤ k|tj| or |tj+1|/|tj| ≤ k t j +1 1
≤ 1 + π−2 ∀ ≥6
j
for all j ≤ n (n=6)? tj 6
< 0.11
If you can find this k, then
k = 0.11, t6 < 3 ×10 −6
k tn
Rn ≤ k tn 0.11
1− k R6 ≤ < ×3 ×10 −6
1 −k 1 −0.11
29

30. Estimation of Truncation Errors
By Integration
If we can find a function f(x) s.t. |tj| ≤ f(j) ∀j ≥ n
and f(x) is a decreasing function ∀x ≥ n, then
∞ ∞
Rn = t n +1 + t n +2 + t n +3 +... = ∑t
j =n +1
j ≤ ∑ f ( j)
j =n +1
∞
Rn ≤ ∫ f ( x )dx
n
30

31. Example (Estimation of Truncation Errors by Integration)
Estimate |Rn| for the following series expansion.
S =∑ j
t where t j = ( j 3 +1) −1
j=1
Solution:
We can pick f(x) = x–3 because it would provide a
tight bound for |tj|. That is
1 1
≥ ∀ ≥1
j
j 3
1+ j3
∞ 1 1
So Rn ≤ ∫ 3
dx =
n x 2n 2
31

32. Alternating Convergent Series
Theorem (Leibnitz Theorem)
If an infinite series satisfies the conditions
– It is strictly alternating.
– Each term is smaller in magnitude than that
term before it.
– The terms approach to 0 as a limit.
Then the series has a finite sum (i.e., converge)
and moreover if we stop adding the terms after the
nth term, the error thus produced is between 0 and
the 1st non-zero neglected term not taken.
32

33. Alternating Convergent Series Theorem
Example 1:
Maclaurin series of ln(1 + x )
∞
x2 x3 x4 xn
S = x − + − + ... = ∑ ( −1) n −1 ( −1 < x ≤ 1)
2 3 4 n =1 n
With n = 5,
1 1 1 1
S = 1 − + − + = 0.7833333340
2 3 4 5
Eerror
ln 2 = 0.693 estimated
1 using the
R = S − ln 2 ≈ 0.09 ≤ = 0.16666 althernating
6 convergent
Actual error series
theorem
33

34. Alternating Convergent Series Theorem
Example 2:
Maclaurin series of cos( x )
x2 x4 x6 ∞
x 2 n +1
S = 1 − + − + ... = ∑ ( −1) n
2! 4! 6! n =0 ( 2n + 1)!
With n = 5,
12 14 16 18
S = 1 − + − + = 0.5403025793
2! 4! 6! 8! Eerror
cos(1) = 0.5403023059 estimated
using the
−7 1 althernating
S − cos(1) = 2.73 × 10 ≤ = 2.76 × 10−7
10! convergent
series
Actual error theorem
34

35. Exercise
If the sine series is to be used to compute sin(1) with an
error less than 0.5x10-14, how many terms are needed?
13 15 17 19 111 113 115 117
sin(1) = 1 − + − + − + − + − ...
3! 5! 7! 9! 11! 13! 15! 17!
R0 R1 R2 R3 R4 R5 R6 R7
Solution:
This series satisfies the conditions of the Alternating
Convergent Series Theorem.
Solving 1 1
Rn ≤ ≤ ×10 −14
( 2n +3)! 2
for the smallest n yield n = 7 (We need 8 terms)
35

36. Exercise
π4 1 1 1
=1 + 4 + 4 + 4 +...
90 2 3 4
How many terms should be taken in order to compute
π4/90 with an error of at most 0.5x10-8?
∞
1 ∞
Rn = tn +1 +tn +2 +... = ∑ < ∫ ( x +1) −4 dx
j= +
n 1 ( j +1) 4 n
Solution −3 ∞integration):
(by −
( x +1) ( n +1)3
= =
−3 n
3
1 1
< ×10 −8 = ( n +1) ≥ 406 = n ≥ 405
> >
3( n +1) 3
2
Note: If we use f(x) = x-3 (which is easier to analyze) instead
of f(x) = (x+1)-3 to bound the error, we will get n >= 406
(just one more term). 36

37. Summary
• Understand what truncation errors are
• Taylor's Series
– Derive Taylor's series for a "smooth" function
– Understand the characteristics of Taylor's Series
approximation
– Estimate truncation errors using the remainder term
• Estimating truncation errors using other methods
– Alternating Series, Geometry series, Integration
37