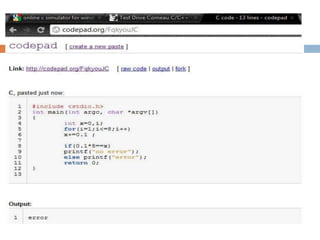
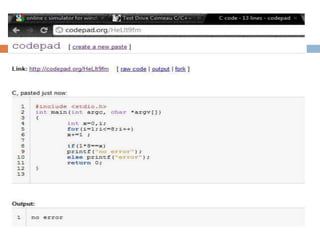
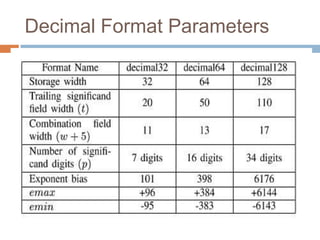
To represent a binary floating-point number as an exact fraction, the number of decimal digits needed depends on the precision of the binary floating-point format. Higher precision formats like double precision may require on the order of 15-17 decimal digits. To represent a binary floating-point number reversibly so that it can be converted back to the same binary value, the number of decimal digits needed depends on the precision as well as the desired rounding mode. For double precision numbers using round-to-nearest rounding, about 16-17 decimal digits are typically needed.

1. DECIMAL
ARITHMETIC
Peeyush Pashine

2. Contents
• Why increasing emphasis on Decimal
Arithmetic?
• Problems caused by Floating Point?
• Disaster ( Examples)
• How Floating to Decimal?
• Is Hardware supports decimal arithmetic
directly?

3. Why Decimal Arithmetic?
 Most computers today support binary floating-
point in hardware.
 But for financial, commercial, and human-
centric (such as Web) applications – NOT
suitable.
 In many commercial applications, including
financial analysis, banking, tax calculation,
currency conversions, insurance, accounting,
and e-commerce, the errors introduced by
converting between decimal and binary
numbers are unacceptable and may violate

4. What problems are caused by
using binary floating-point?
 Binary floating-point cannot exactly represent
decimal fractions.
DECIMAL BINARY
0.9 0.9
0.09 0.089999996
0.009 0.0090
0.0009 9.0E-4
0.00009 9.0E-5
0.000009 9.0E-6
9E-7 9.0000003E-7
9E-8 9.0E-8
9E-9 9.0E-9
9E-10 8.9999996E-10

5. Example
 For example, using the Java or C double datatype,
0.1 × 8 (a binary multiple) gives the result
0.800000000000000044408920985006261616945
2667236328125
 but 0.1 added to itself 8 times gives the different
answer
0.799999999999999933386618522490607574582
09991455078125.
 The two results would not compare equal, and
further, if these values are multiplied by ten and
rounded to the nearest integer below (the „floor‟
function), the result will be 8 in one case and 7 in
the other.

6.  Similarly, the result of 1.30 x 1.05 using binary is
1.3650000000000002131628207280300557613
372802734375; this would be rounded up to
$1.37. However, the result should have been
1.365 – which would be rounded down to $1.36
(using “Banker‟s rounding”).
 Taken over a million transactions of this kind, as
in the „telco‟ benchmark, these systematic errors
add up to an overcharge of more than $20. For a
large company, the million calls might be two-
minutes-worth; over a whole year the error then

7.  for (double d = 0.1; d <= 0.5; d += 0.1)
System.out.println(d);
 for (double d = 1.1; d <= 1.5; d += 0.1)
System.out.println(d);

8. FAILURES

9. The Patriot Missile Failure
 On February 25, 1991, during the Gulf War, an American Patriot Missile
battery in Dharan, Saudi Arabia, failed to track and intercept an incoming
Iraqi Scud missile.
 A report of the General Accounting office, GAO/IMTEC-92-26,
entitled Patriot Missile Defense: Software Problem Led to System Failure
at Dhahran, Saudi Arabia reported on the cause of the failure.
 The cause was an inaccurate calculation of the time since boot due to
computer arithmetic errors.
 Specifically, the time in tenths of second as
measured by the system's internal clock was
multiplied by 1/10 to produce the time in
seconds.

10. Explosion of the Ariane 5
 On June 4, 1996 an unmanned Ariane 5 rocket launched by the European
Space Agency exploded just forty seconds after lift-off (918K QuickTime
movie).
 The cause of the failure was a software error in the inertial reference
system.
 Specifically a 64 bit floating point number relating to
the horizontal velocity of the rocket with respect to the
platform was converted to a 16 bit signed integer. The
number was larger than 32,768, the largest integer
storeable in a 16 bit signed integer, and thus the conversion
failed.

11. The applications actually use
decimal data
 Airline systems, Banking, Financial Analysis,
Insurance, Inventory control, Management
reporting, Marketing services, Order entry,
Order processing, Pharmaceutical
applications, and Retail sales.

12. How much precision and range is
needed for decimal arithmetic?
 This depends, of course, on the application.

13. What rounding modes are needed
for decimal arithmetic?
 The three most important are
 Round-half-even
 Round-half-up
 Round-half-up

14. What disadvantages are there in
using decimal arithmetic?
 Decimal numbers are traditionally held in a
binary coded decimal form which uses about
20% more storage than a purely binary
representation.
 Some properties that hold for binary do not hold
for any other base. For example, (d ÷ 2) × 2
gives d in binary (unless there is an underflow),
but with base 10 it might not if d is full precision
and d ÷ 2 is Inexact.

15. The first division illustrates dividing 2.1 into 123.4 . Since we are working
with integers, this is equivalent to dividing 21 into 1234. The result is 58
and contains no decimal point. This will not give us the precision we
demand in the quotient. In the second division, by shifting the dividend to
the left by one digit (bringing in a 0 on the right), we are effectively dividing
21 into 12340, and producing a quotient of 587 which could be edited to
58.7 for printing.

16.  for (i=0.1; i<0.5; i=i+0.1) printf
("%fn",100000000*i);
 will print out:
 100000001.490116
 200000002.980232
 300000011.920929
 400000005.960464

17. for (num=1.1; num<=1.5; for (num=0.1; num<=0.5;
num=num+0.1) num=num+0.1)
printf ("%fn",num); printf ("%fn",num);
prints: prints:
1.100000 0.100000
1.200000 0.200000
1.300000 0.300000
1.400000 0.400000
0.500000

18. Why doesn’t hardware support
decimal arithmetic directly?
 Most computer architectures other than „pure
RISC‟ machines do, in fact, provide some form
of decimal arithmetic instructions or support.
 The native (hardware) decimal floating-point
arithmetic now available in the IBM Power6
processor and expected in the z6
microprocessor makes programming far
simpler and more robust, and with much better
performance than software

19. DIFFERENT WAYS
INVOLVED

22. Why is decimal arithmetic
unnormalized?
 Unnormalized arithmetic is compatible with
existing languages and applications.
 The arithmetic of all existing decimal datatypes
can be derived by constraining the
unnormalized arithmetic.
 Unnormalized arithmetic often permits
performance improvements.
 Gradual underflow is „free‟.

23. Why is decimal arithmetic
unnormalized?
 Zeros are not special cases.
 Conversions to and from existing decimal
datatypes are faster.
 Unnormalized arithmetic results match human
expectations.
 Application design is simpler.

24. How are decimal numbers
encoded?
 Plimit, the maximum precision of the coefficient. This is the
maximum length of the coefficient, in digits. Any result from an
operation which needs more digits than this will be rounded to fit.
If this rounding caused non-zero digits to be removed, the result
is Inexact.
 Elimit, the maximum encoded exponent. The encoded exponent is
a non-negative number, in the range 0 through Elimit, from which
the exponent parameter is calculated by subtracting a bias. (This
use of a bias makes it easier to compare exponents in a hardware
implementation.)

25. How is the exponent bias
chosen?
 A balanced range of exponents is defined by the parameters,
Emax and Emin, which determine the overflow threshold
(10×10Emax) and the underflow threshold (1×10Emin) respectively.
 In addition to the normal numbers, it must also be possible to
encode a further range of numbers of lower precision which are
smaller than the underflow precision. These numbers are
called subnormal numbers. The smallest subnormal number
must be 1×10Etiny, where Etiny is given by Emin - (Plimit - 1). In our
example format, the range of subnormal numbers is
1×10Etiny through 999999×10Etiny (which is

26. How is the exponent bias
chosen?(cont..)
 In a redundant encoding, more than one coefficient
(with an appropriate exponent) can be used to
represent a given numerical value (for example, the
underflow threshold could be represented as either
1000000×10Etiny or 1×10Emin).
 In a non-redundant encoding, only one coefficient is
used for a given numerical value. (The coefficient
chosen usually depends on the scale – when the scale
is 0 the smallest coefficient is preferred).

27. Decimal Format Parameters

28. Conversion
 How many decimal digits are needed to
represent a binary floating-point number as an
exact fraction?
 How many decimal digits are needed to
represent a binary floating-point number
reversibly?