SG
Uploaded byShiv Prasad Gupta
PPT, PDF11,336 views

Fourier series

This document discusses Fourier series, including definitions, properties, and applications. It describes how to derive Fourier series for various functions, the concept of periodic functions, and conditions under which a function can be expressed as a Fourier series. Additionally, it presents methods for constructing half-range Fourier sine and cosine series, along with examples and problems for further understanding.

Embed presentation

Downloaded 330 times
Contents Euler’s Formula Functions having point of discontinuity Change of interval Even and Odd functions Half Range series Harmonic analysis
FOURIER SERIES Definition of a Fourier series A Fourier series may be defined as an expansion of a function in a series of sine's and cosine’s such as (1) 0 1 ( ) ( cos sin ). 2 n n n a f x a nx b nx ∞ = = + +∑ The coefficients are related to the periodic function f(x) by definite integrals in equation 1. Henceforth we assume f satisfies the following conditions: (1) f(x) is a periodic function; (2) f(x) has only a finite number of finite discontinuities; (3) f(x) has only a finite number of extreme values, maxima and minima in the interval [0,2π]. Fourier series are named in honour of Joseph Fourier (1768-1830), who made important contributions to the study of trigonometric series, in connection with the solution of the heat equation
( ) ( )f t f t T= + where T is a constant and is called the period of the function. A function f(x) which satisfies the relation f(x) = f(x + T) for all real x and some fixed T is called Periodic function. The smallest positive number T, for which this relation holds, is called the period of f(x).  Any function that satisfies Periodic Function
Euler’s Formula The Fourier series for the function f(x) in the interval Is given by - These values of a0,an&bn are known as Euler’s Formula. παα 2+<< x { } ∫ ∫ ∫ ∑ + + + = ∞ = = = ++= πα α πα α πα α π π π 2 2 2 0 1 0 sin)( 1 cos)( 1 )( 1 sincos 2 )( nxdxxfb nxdxxfa dxxfa nxbnxa a xf n n n nn
Problems Q1.Obtain the Fourier series for f(x)=e-x in the interval 0<x<2 . Sol. We know that, π { }∑ ∞ = ++= 1 0 sincos 2 )( n nn nxbnxa a xf { } π π π π π x x x n nn x e ea ea nxbnxa a e 2 2 00 2 0 0 1 0 1 1 1 sincos 2 − − − ∞ = − − = −= = ++= ∫ ∑
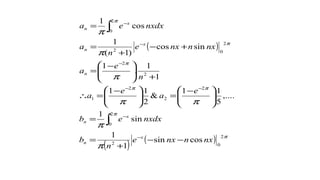
( ) ( ) ( ) π π ππ π π π π π ππ π π π 2 02 2 0 2 2 2 1 2 2 2 02 2 0 cossin 1 1 sin 1 ,.... 5 11 & 2 11 1 1 . 1 sincos )1( 1 cos 1 nxnnxe n b nxdxeb e a e a n e a nxnnxe n a nxdxea x n x n n x n x n −− + = =       − =      − =∴ +      − = +− + = = − − −− − − − ∫ ∫
....... 5 2 . 1 & 2 1 . 1 1 . 1 2 2 2 1 2 2       − =      − =∴ +      − = −− − ππ π ππ π e b e b n ne bn Putting the values of a0,an&bn in the Fourier Series Answer             ++++      ++++ − = − − .....3sin 10 3 2sin 5 2 sin 2 1 .....3cos 10 1 2cos 5 1 cos 2 1 2 11 2 xxxxxx e e x π π
Q2. Find a Fourier series to represent x-x2 from x=- to x= Sol. We know that, π π { }∑ ∞ = ++= 1 0 sincos 2 )( n nn nxbnxa a xf { }∑ ∞ = ++=− 1 02 sincos 2 n nn nxbnxa a xx ∫ ∫ − − − −= − = −= −= π π π π π π π π π π nxdxxxa a xx a dxxxa n cos)( 1 3 2 32 1 )( 1 2 2 0 32 0 2 0
( ) ( ) ( ) ( ) ( ) ( ) n b n nx n nx x n nx xxb nxdxxxb aa n a n nx n nx x n nx xxa n n n n n n n )1(2 cos )2( sin 21 cos1 sin)( 1 ....... 2 4 ; 1 4 14 sin 2 cos 21 sin1 32 2 2 2221 2 32 2 −− =             −+      − ×−−      − −= −= − ==∴ −− =             − −+      − ×−−−= − − − ∫ π π π π π π π π π
;....... 2 2 ; 1 2 21 − =∴ bb Putting this value in Fourier Series, we get Answer       +−+      +−+ − =− ..... 2 2sin 1 sin 2..... 2 2cos 1 cos 4 3 22 2 2 xxxx xx π
Functions having point of discontinuity In the interval (α, α+2π) f(x)= Φ(x), α<x<c = Ψ(x),c<x< α+2π     +=     +=     += ∫ ∫ ∫ ∫ ∫ ∫ + + + c c n c c n c c nxdxxnxdxxb nxdxxnxdxxa dxxdxxa α πα α πα α πα ψφ π ψφ π ψφ π 2 2 2 0 sin)(sin)( 1 cos)(cos)( 1 )()( 1
Problems Q1. Find the Fourier Series expansion for f(x), if f(x)=-π<x<0 x, 0<x< π. Deduce that Sol. We know Then 2 222 85 1 3 1 1 1 π =⋅⋅⋅⋅⋅+++ ∑ ∑ ∞ = ∞ = ++= 1 1 0 sincos 2 )( n n n nxdxbnnxdxa a xf ]| 2 ||[| 1 ])([ 1 0 2 0 0 0 0 π π π π π π π π x xdxdxa +−= +−= − − ∫ ∫ ---A
)1(cos 1 ] 1 cos 1 0[ 1 ] cossinsin [ 1 ]coscos)([ 1 2 ) 2 ( 1 2 22 0 2 0 0 0 2 2 −= −+= ++−= −+−= −= +−= − − − ∫ ∫ π π π π π π π π π π π π π π π π n n n n n n nx n nxx n nx nxdxxnxdxa therefore n
,....... 4 1 ,1, 2 1 ,3 )cos21( 1 ]cos)cos1([ 1 ] sincoscos [ 1 ]sinsin)([ 1 , 5 2 ,0, 3 2 ,0, 1 2 4321 0 2 0 0 0 25423221 − == − ==∴ −= −−= +−+= +−= ⋅ −== ⋅ −== ⋅ − =∴ − −∫ ∫ bbbb n n n n n n n nx n nx x n nx nxdxxnxb therefore aaaaa n π π π π π π π π π π πππ π π π π
....... 4 4sin 3 3sin3 2 2sin sin3...... 5 5cos 3 3cos cos 2 4 )( 22 +−+−+      +++−−= xxx x xx xxf π π Hence putting the values of a’s and b’s in equation –A -----B Hence this is the required result. Putting x=0 in equation B We get, -------C is discontinuous at x=0,       ∞+++−−= ...... 5 1 3 1 1 2 4 )0( 22 π π f )(xf 0)00()00( =+−=−∴ andff π 2 )]00()00([ 2 1 )0( π− =++−=∴ fff
    +++−−=− ..... 5 1 3 1 1 12 42 222 π ππ Hence C equation takes the form
Q2. Find the Fourier Series to represent the function given by for and= for Deduce that Sol. We know that, -----A )(xf xxf =)( ,0 π≤≤ x x−π2 ππ 2≤≤ x 8 .... 5 1 3 1 1 1 2 222 π =∞+++ ∑ ∑ ∞ = ∞ = ++= 1 1 0 sincos 2 )( n n n nxdxbnnxdxa a xf       −−++=     −+=∴         −+=     −+=∴ ∫ ∫ ∫∫ π π π π π π π π π π π π π π π π π π π π 2 2 0 2 0 2 2 2 0 2 2 0 0 sin )2( cossin1 cos)2(cos 1 2 2 2 1 )2( 1 n nx n nx x n nx n nxx nxdxxnxdxxa x x x dxxxdxa n
( ) ( ) ( ) 0 sin)2(sin 1 112 11111 0 2 2 2222 =∴     −+=       −− =∴         − +−        − − ∫ ∫ n n n n nn b nxdxxnxdxxb n a nnnn π π π π π π π Required Fourier Series -------B Put x=a in equation B We get, ∑ ∞ =       −− += 1 2 cos 1)1(2 2 )( n n nx n xf π π
∞+++=⇒ ∞+ − + − + − = ×− =       −− += ∑ ∞ = ...... 5 1 3 1 1 1 8 ...... 5 2 3 2 2 2 4 1)1(2 2 )0( 222 2 22 1 2 π ππ π π n n n f
Half Range Series The Fourier series which contains terms sine or cosine only is known as half range Fourier sine series or half range Fourier cosine series. The function will be defined in range of 0 to but in order to obtain half range Fourier cosine series or half range Fourier sine series we extend the range of the function f(x) or in general (-l,l). So, that the function is either converted in form of even function of even or odd function. Case-1 Half range Fourier cosine series: For the half range Fourier cosine series of the function f(x) in the range (0,l), we extend the function f(x) over the range (-l,l). So that the function become even function. π ),( ππ−
∑ ∞ = += 1 0 cos 2 )( n l xnana xf π ∫= l dxxf l a 0 0 )( 2 ∫       = l n dx l xn xf l a 0 cos)( 2 π Where, Case-2 Half range Fourier sine series: For half range fourier sine series of function f(x),in the range(0,l), we extend the function f(x) over the range (-l,l); so, that the function becomes odd function. ∫ ∑       =       = ∞ = l n n n dx l xn xf l b l xn bxf 0 1 sin)( 2 sin)( π π
Problems Q1. Find the Fourier cosine series for the function f(x)=x2 in the range . Sol. The given function f(x)=x2 is a even function. So, we apply case 1 i.e. π≤≤ x0 ∑ ∞ = += 1 0 cos 2 )( n l xnana xf π ∫       = l n dx l xn xf l a 0 cos)( 2 π [ ] 3 2 3 2 2 1 2 0 0 3 0 0 2 0 2 0 π π π π π π π π = = = = ∫ ∫− a xa dxxa dxxa
[ ] 3 2 3 2 2 1 2 0 0 3 0 0 2 0 2 0 π π π π π π π π = = = = ∫ ∫− a xa dxxa dxxa ( ) ( ) π π π π π π π 0 32 2 0 2 2 sin2cos2sin2 cos 2 cos 1       − + − −= = = ∫ ∫− n nx n nxx n nxx a nxdxxa nxdxxa n n n
∑ ∞ = − += − =     = 1 2 2 2 2 2 cos)1( 4 3 )1(4 cos22 n n n n n n nx x n a n n a π ππ π       −+−−= .......3cos 3 1 2cos 2 1 cos4 3 22 2 2 xxxx π Hence the required result is ,
Q2. Obtain the Fourier expansion of xsinx as a cosine series in (0, ). Hence deduce Sol. Let 4 2 ...... 75 1 53 1 31 1 − =∞− ⋅ + ⋅ − ⋅ π π ( ) ( ) [ ]∫ ∫ ∫ −−+= = = −−−= = π π π π π π π π 0 0 0 00 0 0 )1sin()1sin( 1 cossin 2 2 sin1cos 2 sin 2 dxxnxnxa nxdxxxa a xxxa xdxxa n n
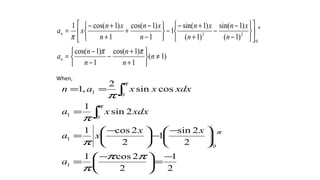
)1( 1 )1cos( 1 )1cos( )1( )1sin( )1( )1sin( 1 1 )1cos( 1 )1cos(1 0 22 ≠       + + − − − =             − − − + +− −       − − + + +− = n n n n n a n xn n xn n xn n xn xa n n ππ π π 2 1 2 2cos1 2 2sin 1 2 2cos1 2sin 1 cossin 2 ,1 1 0 1 0 1 0 1 − =     − =      − −     − = = == ∫ ∫ ππ π π π π π π π a xx xa xdxxa xdxxxan When,
      ∞− ⋅ + ⋅ − ⋅ +=       ∞− ⋅ + ⋅ − ⋅ −−= ...... 75 1 53 1 31 1 21 2 ..... 75 4cos 53 3cos 31 2cos 2cos 2 1 1sin π xxx xxx Putting x= ,then 2 π 4 2 ...... 75 1 53 1 31 1 − =∞− ⋅ + ⋅ − ⋅ π Hence,
Even and Odd Functions:-Even and Odd Functions:- Even function:- 1. The function is said to be even function if 2. The function f(x) is said to be Odd function if
• The graph of odd function is symmetric about origin. • The graph of even function is symmetric about Y-axis. • First we have to check whether the domain of the function is symmetric about the y-axis. How To Determine Whether The Function IsHow To Determine Whether The Function Is Even Or OddEven Or Odd f(x)=sin x -3π -5π/2 -2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2 3π -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 x y 2 5 2:sin π π <<− xx f(x)=sin x -3π -5π/2 -2π -3π/2 -π -π/2 π/2 π 3π/2 2π 5π/2 3π -9 -8 -7 -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 7 8 9 x y
Key Point Products of functions (even)×(even) = (even) (even)×(odd) = (odd) (odd)×(odd) = (even) Sums of functions (even) + (even) = (even) (even) + (odd) = (neither) (odd) + (odd) = (odd)
If Or then the function is even function and then the function is odd function If Function is in this form
Fourier series for even & odd function
Case1:- The Fourier series for the even function F(x) in the interval (-L,+L) is given by
Case2:- If the function f(x) is an odd function then the fourier series (-L,+L) is given by
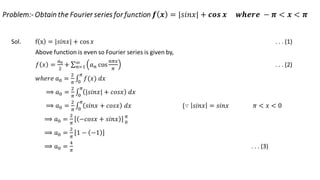
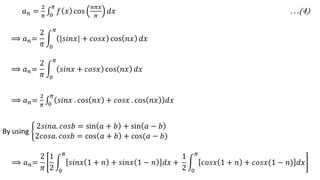
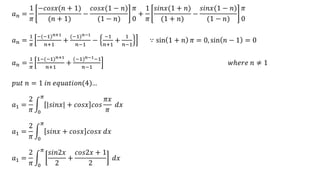
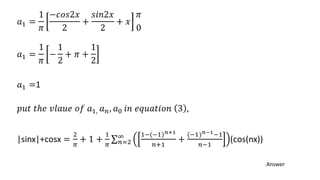
Answer
Half Range Series The Fourier series which contains terms of sine or cosine only is known as half range Fourier sine series or half range Fourier cosine series. The function will be defined in range of 0 to but in order to obtain half range Fourier cosine series or half range Fourier sine series we extend the range of the function f(x) or in general (-l,l). So, that the function is either converted in form of even function of even or odd function. Case-1 Half range Fourier cosine series: For the half range Fourier cosine series of the function f(x) in the range (0,l), we extend the function f(x) over the range (-l,l). So that the function become even function. π ),( ππ−
∑ ∞ = += 1 0 cos 2 )( n l xnana xf π ∫= l dxxf l a 0 0 )( 2 ∫       = l n dx l xn xf l a 0 cos)( 2 π Where, Case-2 Half range Fourier sine series: For half range fourier sine series of function f(x),in the range(0,l), we extend the function f(x) over the range (-l,l); so, that the function becomes odd function. ∫ ∑       =       = ∞ = l n n n dx l xn xf l b l xn bxf 0 1 sin)( 2 sin)( π π
Problems Q1. Find the Fourier cosine series for the function f(x)=x2 in the range . Sol. The given function f(x)=x2 is a even function. So, we apply case 1 i.e. π≤≤ x0 ∑ ∞ = += 1 0 cos 2 )( n l xnana xf π 3 22 0 0 3 3 2 0 0 22 0 21 0 π a πx π a π dxx π a π π dxx π a =    = ∫= ∫−=
[ ] 3 2 3 2 2 1 2 0 0 3 0 0 2 0 2 0 π π π π π π π π = = = = ∫ ∫− a xa dxxa dxxa ( ) ( ) π π π π π π π 0 32 2 0 2 2 sin2cos2sin2 cos 2 cos 1       − + − −= = = ∫ ∫− n nx n nxx n nxx a nxdxxa nxdxxa n n n and, ∫       = l n dx l xn xf l a 0 cos)( 2 π
∑ ∞ = − += − =     = 1 2 2 2 2 2 cos)1( 4 3 )1(4 cos22 n n n n n n nx x n a n n a π ππ π       −+−−= .......3cos 3 1 2cos 2 1 cos4 3 22 2 2 xxxx π Hence the required result is ,
Q2. Obtain the Fourier expansion of xsinx as a cosine series in (0, ). Hence deduce Sol. Let 4 2 ...... 75 1 53 1 31 1 − =∞− ⋅ + ⋅ − ⋅ π π ( ) ( ) [ ]∫ ∫ ∫ −−+= = = −−−= = π π π π π π π π 0 0 0 00 0 0 )1sin()1sin( 1 cossin 2 2 sin1cos 2 sin 2 dxxnxnxa nxdxxxa a xxxa xdxxa n n
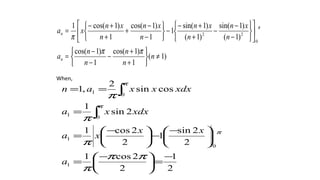
)1( 1 )1cos( 1 )1cos( )1( )1sin( )1( )1sin( 1 1 )1cos( 1 )1cos(1 0 22 ≠       + + − − − =             − − − + +− −       − − + + +− = n n n n n a n xn n xn n xn n xn xa n n ππ π π 2 1 2 2cos1 2 2sin 1 2 2cos1 2sin 1 cossin 2 ,1 1 0 1 0 1 0 1 − =     − =      − −     − = = == ∫ ∫ ππ π π π π π π π a xx xa xdxxa xdxxxan When,
      ∞− ⋅ + ⋅ − ⋅ +=       ∞− ⋅ + ⋅ − ⋅ −−= ...... 75 1 53 1 31 1 21 2 ..... 75 4cos 53 3cos 31 2cos 2cos 2 1 1sin π xxx xxx Putting x= ,then 2 π 4 2 ...... 75 1 53 1 31 1 − =∞− ⋅ + ⋅ − ⋅ π Hence,
Harmonic Analysis The process of finding the Fourier series corresponding to the function when the function by numerical values is known as harmonic analysis. The Fourier series for the function f(x) in the interval is given by- If the given function is not the explicit function of the independent variable x and the function is defined by the numerical values then the formula of a0,an and bn are given by the following relations. ∫ ∫ ∫ ∑ + + + ∞ =       =       = =             +      += c n c n c n nn dx c xn xf c b dx c xn xf c a dxxf c a c xn b c xn a a xf 2 2 2 0 1 0 sin)( 1 cos)( 1 )( 1 sincos 2 )( α α α α α α π π ππ Where, cx 2+<< αα
a0 = 2x[Mean value of f(x) in the interval ( )] an = 2x[Mean value of in the interval( )] bn = 2x[Mean value of in the interval ( )] In formula 1 the first term of expansion is known as first or fundamental harmonic. The second term is known as second harmonic and the term is known as third harmonic and so on….. c2, +αα       ⋅ c xn xf π cos)( c2, +αα       ⋅ c xn xf π sin)( c2, +αα c xb c xa n ππ sincos1 + c xb c xa ππ 2sin2cos 22 + c xb c xa ππ 3sin3cos 33 +
Problems Q1. In a machine the displacement y of a given point is given for a certain angle as follows. Find the coefficient of in the Fourier series representing the above variations. Sol. The Fourier series for the function y in the given interval 0-360o or ( ) is given by θ 0 30 60 90 120 150 180 210 240 270 300 350 7.9 8 7.2 5.6 3.6 1.7 0.5 0.2 0.9 2.5 4.7 6.8 °θ y ( ).sincos 2 1 0 ∑ ∞ = ++= n nn xnbxna a y ππ π2,0 θ2sin
Presented By :- Shiv Prasad Gupta Naveen Kumar Avinash

More Related Content

PPTX
Fourier series
byPinky Chaudhari
 
PPTX
the fourier series
bysafi al amu
 
PPTX
Fourier series
bykishor pokar
 
PPTX
Fourier series and its applications by md nazmul islam
byMd Nazmul Islam
 
PPT
Fourier series
byNaveen Sihag
 
PPTX
Fourier Series - Engineering Mathematics
byMd Sadequl Islam
 
PPTX
Fourier series
bySanthanam Krishnan
 
PPTX
Application of fourier series
byGirish Dhareshwar
 
Fourier series
byPinky Chaudhari
 
the fourier series
bysafi al amu
 
Fourier series
bykishor pokar
 
Fourier series and its applications by md nazmul islam
byMd Nazmul Islam
 
Fourier series
byNaveen Sihag
 
Fourier Series - Engineering Mathematics
byMd Sadequl Islam
 
Fourier series
bySanthanam Krishnan
 
Application of fourier series
byGirish Dhareshwar
 

What's hot

PPTX
Fourier series Introduction
byRizwan Kazi
 
PPTX
Partial differentiation B tech
byRaj verma
 
PPTX
AEM Fourier series
bySiddhi Viradiya
 
PPTX
Series solution to ordinary differential equations
byUniversity of Windsor
 
PDF
Dcs lec02 - z-transform
byAmr E. Mohamed
 
PDF
Laplace transform
byAMIE(I) Study Circle
 
PPTX
Fourier integral
byVikshit Ganjoo
 
PDF
Fourier series and transforms
byPepa Vidosa Serradilla
 
PDF
Newton's Forward/Backward Difference Interpolation
byVARUN KUMAR
 
PPT
fourier transforms
byUmang Gupta
 
PDF
Fourier Series
bySimmiRockzz
 
PPTX
Discrete Fourier Transform
byAbhishek Choksi
 
PDF
Numerical Differentiation and Integration
byMeenakshisundaram N
 
PPTX
Discrete Time Fourier Transform
byWaqas Afzal
 
PPTX
Radix-2 DIT FFT
bySarang Joshi
 
PPT
aem : Fourier series of Even and Odd Function
bySukhvinder Singh
 
PDF
fourier series
by8laddu8
 
PPTX
Laplace transform
by001Abhishek1
 
PPTX
Vector Spaces,subspaces,Span,Basis
byRavi Gelani
 
PPTX
Z transforms and their applications
byRam Kumar K R
 
Fourier series Introduction
byRizwan Kazi
 
Partial differentiation B tech
byRaj verma
 
AEM Fourier series
bySiddhi Viradiya
 
Series solution to ordinary differential equations
byUniversity of Windsor
 
Dcs lec02 - z-transform
byAmr E. Mohamed
 
Laplace transform
byAMIE(I) Study Circle
 
Fourier integral
byVikshit Ganjoo
 
Fourier series and transforms
byPepa Vidosa Serradilla
 
Newton's Forward/Backward Difference Interpolation
byVARUN KUMAR
 
fourier transforms
byUmang Gupta
 
Fourier Series
bySimmiRockzz
 
Discrete Fourier Transform
byAbhishek Choksi
 
Numerical Differentiation and Integration
byMeenakshisundaram N
 
Discrete Time Fourier Transform
byWaqas Afzal
 
Radix-2 DIT FFT
bySarang Joshi
 
aem : Fourier series of Even and Odd Function
bySukhvinder Singh
 
fourier series
by8laddu8
 
Laplace transform
by001Abhishek1
 
Vector Spaces,subspaces,Span,Basis
byRavi Gelani
 
Z transforms and their applications
byRam Kumar K R
 

Similar to Fourier series

PPTX
Fourier series and fourier integral
byashuuhsaqwe
 
PPT
1531 fourier series- integrals and trans
byDr Fereidoun Dejahang
 
PDF
Half range sine and cosine series
byChandan S
 
PPTX
senior seminar
byJose Stewart
 
PPTX
Topic: Fourier Series ( Periodic Function to change of interval)
byAbhishek Choksi
 
PDF
lecture_6_-_fourier_series_0.pdf
byHendIbrahim35
 
PDF
Math 1102-ch-3-lecture note Fourier Series.pdf
byhabtamu292245
 
DOCX
Important Questions of fourier series with theoretical study Engg. Mathem...
byMohammad Imran
 
PDF
PDF ppt fourier series and Fourier transforms .pdf
byalexander825344
 
PPTX
mukul pptx 2.pptx mathematics laplace pptx engineering mathematics 2
byMukulKumar596365
 
PPTX
half range sine and cosine series.pptx(Test for Convergence.pptx(Sequence and...
bydurgesh351287
 
PPT
Fourier series 2.ppt
byBlisterCount
 
PPTX
Fourier_Series.pptx
byAliNadeem48
 
PPTX
Mathematics basics
byVivek Kumar Sinha
 
PDF
04. Even and Odd Cases of Fourier Series.pdf
bymoshiourrahmanmohib1
 
PDF
ilovepdf_merged.pdf
byNaorinHalim
 
PPTX
PS.pptx
byraj20072
 
PPTX
FOURIER SERIES Presentation of given functions.pptx
byjyotidighole2
 
PPS
Unit vii
bymrecedu
 
PDF
Mba Ebooks ! Edhole
byEdhole.com
 
Fourier series and fourier integral
byashuuhsaqwe
 
1531 fourier series- integrals and trans
byDr Fereidoun Dejahang
 
Half range sine and cosine series
byChandan S
 
senior seminar
byJose Stewart
 
Topic: Fourier Series ( Periodic Function to change of interval)
byAbhishek Choksi
 
lecture_6_-_fourier_series_0.pdf
byHendIbrahim35
 
Math 1102-ch-3-lecture note Fourier Series.pdf
byhabtamu292245
 
Important Questions of fourier series with theoretical study Engg. Mathem...
byMohammad Imran
 
PDF ppt fourier series and Fourier transforms .pdf
byalexander825344
 
mukul pptx 2.pptx mathematics laplace pptx engineering mathematics 2
byMukulKumar596365
 
half range sine and cosine series.pptx(Test for Convergence.pptx(Sequence and...
bydurgesh351287
 
Fourier series 2.ppt
byBlisterCount
 
Fourier_Series.pptx
byAliNadeem48
 
Mathematics basics
byVivek Kumar Sinha
 
04. Even and Odd Cases of Fourier Series.pdf
bymoshiourrahmanmohib1
 
ilovepdf_merged.pdf
byNaorinHalim
 
PS.pptx
byraj20072
 
FOURIER SERIES Presentation of given functions.pptx
byjyotidighole2
 
Unit vii
bymrecedu
 
Mba Ebooks ! Edhole
byEdhole.com
 

Recently uploaded

PDF
Python Frameworks for Machine Learning Labmanuel
bygomathisankariv2
 
PDF
22PEOIT4C Artificial Intelligence unit 3 QB Final.pdf
byGuru Nanak Technical Institutions
 
PDF
22PE0IT4C_Artificial_Intelligence_Unit_1_QB_Final
byGuru Nanak Technical Institutions
 
PPTX
22PEOIT4C Unit 3 Session 18 First Order Logic.pptx
byGuru Nanak Technical Institutions
 
PDF
22PEOIT4C_Artificial_Intelligence_UNIT_III_Notes_Final
byGuru Nanak Technical Institutions
 
PDF
Performance Benchmarking Strategies for AI/HPC/EdgeAI
byDanny Jiang
 
PPTX
Operational Amplifier (op - amp), types of op amp
byVaishaliVaishali14
 
PDF
TU/e - 2025-2026 - Lecture Geotechnics 3 - Arkesteijn
byRuud Arkesteijn
 
PDF
BCS402 MICROCONTROLLERS MODULE 1
byAbhijith L Kotian
 
PDF
Operating system Introduction to System Call
bySanjay Gunjal
 
PPTX
uCOS_II_LED_Multitasking_Exp.no.2.pptx uCOS_II_LED_Multitasking_Exp.no.2.pptx
bySanjivani College of Engineering, Kopargaon, Ahmednagar, Maharashtra, India
 
PDF
Software Engineering : Process Model
byGunjalSanjay
 
PPTX
1.1 Structure of Materials_Material science.pptx
byDr. Sandip Thorat
 
PDF
Introduction : Operating-System Services
bySanjay Gunjal
 
PPTX
TechSprint Intro Session GDGOC PUSSGRC
bykashvidua39
 
PPTX
TEST presentation to see if I can share it with notes.
byFernando Benavides
 
PPTX
PEMET 413 KTU 2024 SCHEME MODULE 2 LECTURE 4.pptx
byVINAY B
 
PPTX
PEMET 413 KTU 2024 MODULE 2 LECTURE 3.pptx
byVINAY B
 
PPTX
1.2-Structure of Ceramics_ Materials Science.pptx
byDr. Sandip Thorat
 
PPTX
Starter Generator Testing – Why It Is Critical for Aerospace & Defence Platforms
byNeometrix_Engineering_Pvt_Ltd
 
Python Frameworks for Machine Learning Labmanuel
bygomathisankariv2
 
22PEOIT4C Artificial Intelligence unit 3 QB Final.pdf
byGuru Nanak Technical Institutions
 
22PE0IT4C_Artificial_Intelligence_Unit_1_QB_Final
byGuru Nanak Technical Institutions
 
22PEOIT4C Unit 3 Session 18 First Order Logic.pptx
byGuru Nanak Technical Institutions
 
22PEOIT4C_Artificial_Intelligence_UNIT_III_Notes_Final
byGuru Nanak Technical Institutions
 
Performance Benchmarking Strategies for AI/HPC/EdgeAI
byDanny Jiang
 
Operational Amplifier (op - amp), types of op amp
byVaishaliVaishali14
 
TU/e - 2025-2026 - Lecture Geotechnics 3 - Arkesteijn
byRuud Arkesteijn
 
BCS402 MICROCONTROLLERS MODULE 1
byAbhijith L Kotian
 
Operating system Introduction to System Call
bySanjay Gunjal
 
uCOS_II_LED_Multitasking_Exp.no.2.pptx uCOS_II_LED_Multitasking_Exp.no.2.pptx
bySanjivani College of Engineering, Kopargaon, Ahmednagar, Maharashtra, India
 
Software Engineering : Process Model
byGunjalSanjay
 
1.1 Structure of Materials_Material science.pptx
byDr. Sandip Thorat
 
Introduction : Operating-System Services
bySanjay Gunjal
 
TechSprint Intro Session GDGOC PUSSGRC
bykashvidua39
 
TEST presentation to see if I can share it with notes.
byFernando Benavides
 
PEMET 413 KTU 2024 SCHEME MODULE 2 LECTURE 4.pptx
byVINAY B
 
PEMET 413 KTU 2024 MODULE 2 LECTURE 3.pptx
byVINAY B
 
1.2-Structure of Ceramics_ Materials Science.pptx
byDr. Sandip Thorat
 
Starter Generator Testing – Why It Is Critical for Aerospace & Defence Platforms
byNeometrix_Engineering_Pvt_Ltd
 

Fourier series