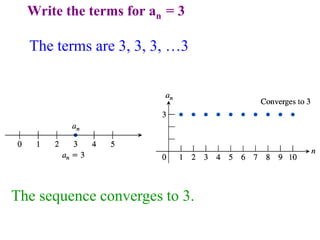
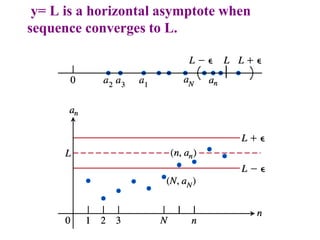
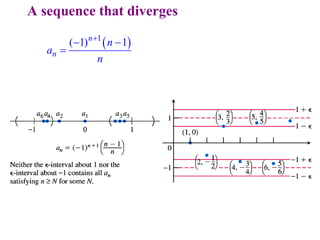
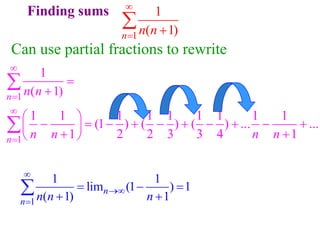
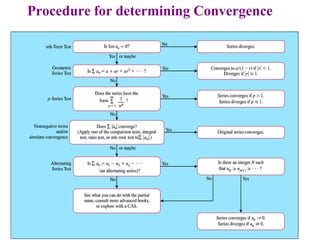
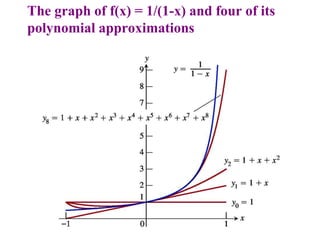
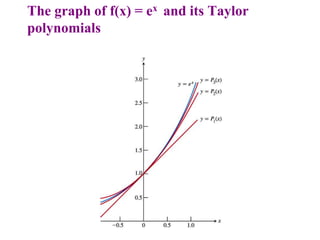
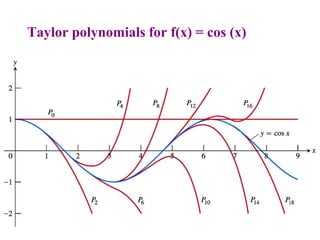
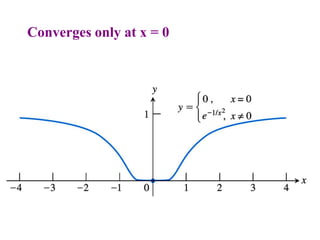
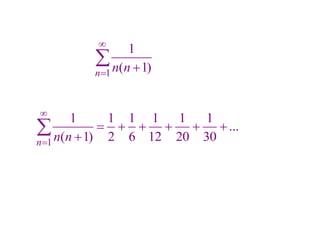This document discusses convergence of sequences and series. It defines a sequence as an ordered list of objects and describes how to write the first few terms. A sequence converges if its terms get closer to a single value, while a divergent sequence does not. Infinite series represent the sum of the terms in a sequence. A series converges if the partial sums converge to a finite limit. Geometric series have a common ratio between terms and their sums can be determined based on this ratio. The integral test can be used to determine if a series converges by comparing it to a corresponding integral.

1. CONVERGENCE OF A SEQUENCE

2. 12. 1 A sequence is…
(a) an ordered list of objects.
(b) A function whose domain is a set of integers.
Domain: 1, 2, 3, 4, …,n…
Range a1, a2, a3, a4, … an…
1 1 1 1
1, , , , ...
2 4 8 16
{(1, 1), (2, ½), (3, ¼), (4, 1/8) ….}

3. Finding patterns
Describe a pattern for each sequence. Write
a formula for the nth term
1 1 1 1
1, , , , ...
2 4 8 16
1 1 1 1
1, , , , ...
2 6 24 120
1 4 9 16 25
, , , , ...
4 9 16 25 36
1
1
2n
1
!
n
2
2
( 1)
n
n 

4. Write the first 5 terms for
1 2 3 4 1
0, , , , ... ...
2 3 4 5
n
n

The terms in this sequence get closer and closer
to 1. The sequence CONVERGES to 1.
On a number line As a function
1
n
n
a
n



5. Write the first 5 terms
1 2 3 4 1
0, , , , . ... ...
2 3 4 5
n
n

    
The terms in this sequence do not get close to
Any single value. The sequence Diverges
 
1
( 1) 1
n
n
n
a
n

 


6. Write the terms for an = 3
The terms are 3, 3, 3, …3
The sequence converges to 3.

7. y= L is a horizontal asymptote when
sequence converges to L.

8. A sequence that diverges
 
1
( 1) 1
n
n
n
a
n

 


9. Sequences
Write the first 5 terms of the sequence.
Does the sequence converge? If so, find the value.
1
( 1)
2 1
n
n
a
n




1 1 1 1
1, , , ,
3 5 7 9
 
1
( 1)
lim 0
2 1
n
n
n





1 1
( 1) 1
n
n
a
n
  
  
 
 
1 2 3 4
0, , , ,
2 3 4 5
  
1
lim ( 1) 1
n
n does not exist
n

 
 
 
 
The sequence converges to 0.
The sequence diverges.

10. 12.2 Infinite Series
1
1 1 1 1 1
...
2 4 8 16
2n
n


    

1
1 1 1 1 1 ...
n


    

The series diverges because sn = n. Note that the
Sequence {1} converges.
Represents the sum of the terms in a sequence.
We want to know if the series converges to
a single value i.e. there is a finite sum.

11. 1
1
( 1)
n n n

 

1
1 1 1 1 1 1
...
( 1) 2 6 12 20 30
n n n


     



12. Partial sums of
1
1
1
1
2
2
s  

2
2
3
1 1
1 2 2 3
s   
 
3
1 1 1
1 2 2 4
4
3
3 3
s    
  
1 1 1 1
...
1 2 2 3 3 4 ( 1 1
)
n
n
s
n n
n
    
   

If the sequence of partial sums converges,
the series converges
and
1 2 3 4 5
, , , , ... ...
2 3 4 5 6 1
n
n 
Converges to 1 so series converges.
1
1 1 1 1 1 1
...
( 1) 2 6 12 20 30
n n n


     



13. Finding sums
1
1
( 1)
n n n

 

1
1
1
( 1)
1 1 1 1 1 1 1 1 1
(1 ) ( ) ( ) ... ...
1 2 2 3 3 4 1
n
n
n n
n n n n






 
         
 
 
 


Can use partial fractions to rewrite
1
1 1
lim (1 ) 1
( 1) 1
n
n n n n



  
 


14. .
The partial sums of the series
1
1
( 1)
n n n

 

Limit

15. Geometric Series
1
1 1 1 1 1
...
2 4 8 16
2n
n


    

Each term is obtained from the preceding
number by multiplying by the same number r.
1 1 1 1
...
5 25 125 625
   
2 4 8 16
...
3 3 3 3
   
Find r (the common ratio)

16. Is a Geometric Series
1 1 1 1
...
2 4 8 16
   
3 12 48 192
...
5 25 125 625
   
2 4 8 16
...
3 3 3 3
   
1
1
n
n
ar



 Where a = first term and r=common ratio
Write using series notation
1
1
1 1
2 2
n
n



 
 
 

1
1
3 4
5 5
n
n



 

 
 

  1
1
2
2
3
n
n





17. The sum of a geometric series
2 3
... n
n
rs ar ar ar ar
   
2 3 1
... n
n
s a ar ar ar ar 
    
n
n n
s rs a ar
  
(
1
1
1
,
)
1
n
n
n
a ar
s
a r
r
r
r



  

1 .
| 0
| , n
r as n
if r 
  
| | 1
1
,
n
a
s r
r
 

Geometric series converges to
If r>1 the geometric series diverges.
Multiply each term by r
Sum of n terms
subtract

18. Find the sum of a Geometric Series
1
1
, | | 1
1
n
n
a
ar r
r



 


Where a = first term and r=common ratio
1
1
1 1
2 2
n
n



 
 
 

1
1
3 4
5 5
n
n



 

 
 

  1
1
2
2
3
n
n



 The series diverges.
1
2 1
1
1
2

 3
3 1
5
4 9 3
1
5
 


19. Repeating decimals-Geometric Series
2 4 6 8
8 8 8 8
0.080808 ...
10 10 10 10
    
2
1
1
2
8
8
10
1
1 99
1
10
n
n
a
ar
r



  
 

The repeating decimal is equivalent to 8/99.
2 2
8 1
10 10
a and r
 
1
1
2 2
1 1
8 1
10 10
n
n
n n
ar

 

 
 
  
 
 

20. Series known to converge or diverge
1. A geometric series with | r | <1 converges
2. A repeating decimal converges
3. Telescoping series converge
A necessary condition for convergence:
Limit as n goes to infinity for nth term
in sequence is 0.
nth term test for divergence:
If the limit as n goes to infinity for the nth
term is not 0, the series DIVERGES!

21. Convergence or Divergence?
1
10
10 1
n
n
n





1
1 1
2
n n n





 
1
1.075
n
n


 1
4
2n
n




22. A series of non-negative terms converges
If its partial sums are bounded from above.
A sequence in which each term is less than or
equal to the one before it is called a monotonic
non-increasing sequence. If each term is greater
than or equal to the one before it, it is called
monotonic non-decreasing.
A monotonic sequence that is bounded
Is convergent.

23. 12. 3 The Integral Test
Let {an} be a sequence of positive terms.
Suppose that an = f(n) where f is a continuous
positive, decreasing function of x for all xN.
Then the series and the corresponding integral
shown both converge of both diverge.
n
n N
a


 ( )
N
f x dx


f(n) f(x)

24. The series and the integral both converge or both diverge
Exact area under curve is between
If area under curve is finite, so is area in rectangles
If area under curve is infinite, so is area in rectangles
Area in rectangle corresponds to term in sequence

25. Using the Integral test
2
1 1
n
n
n

 

2
2 2 1
1 1
2
1 2
lim lim ln( 1)
2
1 1
lim (ln( 1) ln2)
b b
b b
b
x x
dx dx x
x x
b

 

 
  
 
 
   
 
Thus the series diverges
2
( )
1
n
n
a f n
n


 2
(
1
)
x
f
x
x 

The improper integral diverges

26. Using the Integral test
2
1
1
1
n n

 

 
2 2 1
1 1
1 1
lim lim arctan
1 1
lim (arctan arctan1)
2 4 4
b
b
b b
b
dx dx x
x x
b
  

 

 
 
   
 
Thus the series converges
2
( )
1
1
n
a f n
n
 

2
1
( )
1
f x
x


The improper integral converges

27. Harmonic series and p-series
1
1
p
n n


 Is called a p-series
A p-series converges if p > 1 and diverges
If p < 1 or p = 1.
1
1 1 1 1 1 1
1 .... ....
2 3 4 5
n n n


      

Is called the harmonic series and it
diverges since p =1.

28. 1
1 3
1
n
n



Identify which series converge and which diverge.
1
1
n n



1 3
1
n
n




1
1
n n



2
1
100
n n



1
1
3 4
5 5
n
n



 

 
 


29. 12. 4Direct Comparison test
Let
1
n
n
a


 be a series with no negative terms
1
n
n
a


 Converges if there is a series
Where the terms of an are less than or equal to
the terms of cn for all n>N.
1
n
n
c



1
n
n
a


 Diverges if there is a series
Where the terms of an are greater than or equal
to the terms of dn for all n>N.
1
n
n
d




30. Limit Comparison test
both converge or both diverge:
Limit Comparison test
lim , 0
n
x
n
a
c c
b
    
Then the following series
1
n
n
a


 1
n
n
b



and
lim 0
n
x
n
a
b
 
Amd
1
n
n
b


 Converges then
1
n
n
a


 Converges
lim n
x
n
a
b
  
1
n
n
b


 Diverges then 1
n
n
a


 Diverges
and
and

31. Convergence or divergence?
1
1
2 3n
n

 

2
1 1
n
n
n

 

1
1
3 2
n n

 


32. Alternating Series
A series in which terms alternate in sign
1
( 1)n
n
n
a



 1
1
( 1)n
n
n
a





or
1
1
1 1 1 1 1
( 1) ...
2 4 8 16
2
n
n
n



     

1
1 1 1 1
( 1) 1 ...
2 3 4
n
n n


     


33. Alternating Series Test
1
1 2 3 4
1
( 1) ...
n
n
n
a a a a a



     

Converges if:
an is always positive
an an+1 for all n  N for some integer N.
an0
If any one of the conditions is not met, the
Series diverges.

34. Absolute and Conditional Convergence
• A series is absolutely convergent if the
corresponding series of absolute values
converges.
• A series that converges but does not converge
absolutely, converges conditionally.
• Every absolutely convergent series converges.
(Converse is false!!!)
n
n N
a



n
n N
a




35. Is the given series convergent or divergent? If it is
convergent, its it absolutely convergent or
conditionally convergent?
( 1) / 2
1
( 1)
3
n n
n
n




 1
( 1)
ln( 1)
n
n n





1
( 1)n
n n




1
1
( 1) ( 1)
n
n
n
n



 


36. a) Is the given series convergent or divergent? If
it is convergent, its it absolutely convergent or
conditionally convergent?
( 1) / 2
1
( 1) 1 1 1 1
...
3 9 27 81
3
n n
n
n




     

This is not an alternating series, but since
( 1) / 2
1 1
( 1) 1
3 3
n n
n n
n n

 
 


 
Is a convergent geometric series, then the given
Series is absolutely convergent.

37. b) Is the given series convergent or divergent? If
it is convergent, its it absolutely convergent or
conditionally convergent?
1
( 1) 1 1 1
......
ln( 1) ln 2 ln3 ln 4
n
n n



    


Diverges with direct comparison with the harmonic
Series. The given series is conditionally convergent.
1
( 1) 1 1 1
......
ln( 1) ln 2 ln3 ln 4
n
n n



   


Converges by the Alternating series test.

38. c) Is the given series convergent or divergent? If
it is convergent, its it absolutely convergent or
conditionally convergent?
1
1
( 1) ( 1) 2 3 4 5
1 2 3 4
n
n
n
n



 
    

By the nth term test for divergence, the series
Diverges.

39. d) Is the given series convergent or divergent? If
it is convergent, its it absolutely convergent or
conditionally convergent?
1
( 1) 1 1 1 1
1 2 3 4
n
n n



    

Converges by the alternating series test.
1
( 1) 1 1 1 1
1 2 3 4
n
n n



   

Diverges since it is a p-series with p <1. The
Given series is conditionally convergent.

40. The Ratio Test
Let be a series with positive terms and
n
n N
a



1
lim n
n
n
a
a


 
Then
• The series converges if ρ < 1
• The series diverges if ρ > 1
• The test is inconclusive if ρ = 1.

41. The Root Test
Let be a series with non-zero terms and
n
n N
a



lim | |
n
n n
a L
 
Then
• The series converges if L< 1
• The series diverges if L > 1 or is infinite
• The test is inconclusive if L= 1.

42. 1
2
!
n
n n



2 1
1
3
2
n
n
n n




Convergence or divergence?
2
1
n
n
n
e
n




43. . Procedure for determining Convergence

44. Power Series (infinite polynomial in x)
2
0 1 2
0
..... ...
n n
n n
n
c x c c x c x c x


   

2
0 1 2
0
( ) ( ) ( ) ..... ( ) ...
n n
n n
n
c x a c c x a c x a c x a


       

Is a power series centered at x = 0.
Is a power series centered at x = a.
and

45. Examples of Power Series
2 3
0
1 ...
! 2 3!
n
n
x x x
x
n


    

2
0
( 1) 1 1 1
( 1) 1 ( 1) ( 1) ..... ( 1) ...
3 9
3 3
n
n n
n n
n
x x x x



       

Is a power series centered at x = 0.
Is a power series centered at x = -1.
and

46. Geometric Power Series
2 3 4
0
1 ...
n n
n
x x x x x x


     

1
, 1
1 1
1
a
S x
r x
a and r x
 
  
 
1
2
2
2 3
3
1
1
1
P x
P x x
P x x x
 
  
   

47. . The graph of f(x) = 1/(1-x) and four of its
polynomial approximations

48. Convergence of a Power Series
There are three possibilities
1)There is a positive number R such that the
series diverges for |x-a|>R but converges for
|x-a|<R. The series may or may not converge
at the endpoints, x = a - R and x = a + R.
2)The series converges for every x. (R = .)
3)The series converges at x = a and diverges
elsewhere. (R = 0)

49. What is the interval of convergence?
0
( 1)n
n




Since r = x, the series converges |x| <1, or
-1 < x < 1. In interval notation (-1,1).
Test endpoints of –1 and 1.
0
(1)n
n



Series diverges
Series diverges
2 3 4
0
1 ...
n n
n
x x x x x x


     


50. Geometric Power Series
1 3 3
1 3 ( 1) 4
1
1
1 ( 1)
3
1
( 1)
3
a and r x
x
a
S
r x x
  
   


   

2
0
( 1) 1 1 1
( 1) 1 ( 1) ( 1) ..... ( 1) ...
3 9
3 3
n
n n
n n
n
x x x x



       

1
( 1
3
1
1 1
)
( )
3
r x
x
  
 

Find the function
Find the radius of convergence
2 4
x
  

51. Geometric Power Series
0
( 1)
( 1)
3
n
n
n
n
x





Find the radius of convergence
Find the interval of convergence
For x = -2,
0 0 0
( 1) ( 1) ( 1) 1
( 2 1)
3 3 3
n n n
n
n n n
n n n
  
  
  
   
  
Geometric series with r < 1, converges
0 0 0 0
( 1) ( 1) ( 3) 3
( 4 1) 1
3 3 3
n n n n
n
n n n
n n n n
   
   
  
    
   
By nth term test, the series diverges.
For x = 4
2 4
x
  
Interval of convergence

52. Finding interval of convergence
1
x 
Use the ratio test:
1
1
1
n n
n n
x x
u and u
n n


 

1
1
lim lim
1
n
n
n n n
n
u x n
x
u n x


 
 

R=1
For x = 1 For x = -1
0
n
n
x
n



(-1, 1)
0
1
n n


 0
( 1)n
n n




Harmonic series
diverges
Alternating Harmonic series
converges
1
1
lim lim
1
n
n
n n n
n
u x n
x
u n x


 
 

[-1, 1)
Interval of convergence

53. Differentiation and Integration of Power Series
2
0 1 2
0
( ) ( ) ( ) ..... ( ) ...
n n
n n
n
c x a c c x a c x a c x a


       

If the function is given by the series
Has a radius of convergence R>0, the on the
interval (c-R, c+R) the function is continuous,
Differentiable and integrable where:
1
0
( ) ( )n
n
n
f x nc x a



  

0
( )
( )
1
n
n
n
x a
f x dx C c
n



 



The radius of convergence is the same but the
interval of convergence may differ at the endpoints.

54. Constructing Power Series
If a power series exists has a radius of convergence = R
It can be differentiated
2
0 1 2
( ) ( ) ( ) ..... ( ) ...
n
n
f x c c x a c x a c x a
      
2 1
1 2 3
( ) 2 ( ) 3 ( ) ..... ( ) ...
n
n
f x c c x a c x a nc x a 
      
2
2 3
( ) 2 2*3 ( ) 3* 4( ) ....
f x c c x a x a
     
2
3 4
( ) 1* 2*3 2*3* 4 ( ) 3* 4*5( ) ...
f x c c x a x a
      
( )
( ) ! ( )
n
n
f x n c terms with factor of x a
  
So the nth derivative is

55. ( )
( ) ! ( )
n
n
f x n c terms with factor of x a
  
All derivatives for f(x) must equal the series
Derivatives at x = a.
1
2
3
( )
( ) 1* 2
( ) 1* 2 *3
f a c
f a c
f a c
 
 
 
( )
( ) !
n
n
f a n c

( )
( )
!
n
n
f a
c
n

Finding the coefficients for a Power Series

56. ( )
2 3
0
( )
( ) ( ) ( )
( ) ( ) ( ) ( ) ...
! 2! 3!
( )
...
!
k
k
n
n
f a f a f a
f a f x a x a x a
k
f a
x
n


 

      
 

If f has a series representation centered at x=a, the
series must be
If f has a series representation centered at x=0, the
series must be
( )
2 3
0
( )
(0) (0) (0)
( ) (0) ( ) ( ) ...
! 2! 3!
(0)
...
!
k
k
n
n
f f f
f a f x a x a
k
f
x
n


 

     
 


57. Form a Taylor Polynomial of order 3 for
sin x at a =
n f(n)(x) f(n)(a) f(n)(a)/n!
0 sin x
1 cos x
2 -sin x
3 -cos x
2
2
2
2
2
2

2
2

2
2
2
2
2
2 * 2!

2
2 *3!

4


58. The graph of f(x) = ex and its Taylor
polynomials

59. 2 3 4
0
1 ...
! 2 3! 4!
n
n
x x x x
x
n


     

Find the derivative and the integral
  2 1 3 5 7
0
1
...
(2 1)! 3! 5! 7!
n n
n
x x x x
x
n




   



60. Taylor polynomials for f(x) = cos (x)

61. Converges only at x = 0