This document contains information about a Laplace transform topic presentation including: - The names and enrollment numbers of 8 students working on the topic. - The definition of the Laplace transform and some elementary functions transformed. - Theorems on shifting, differentiation, integration, and multiplication of Laplace transforms. - Examples of using Laplace transforms to evaluate integrals and find derivatives. - The application of Laplace transforms to differential equations.

1. HUMANITIES AND SCIENCE DEPARTMENT.
SARDAR PATEL COLLEGE OF
ENGINEERING,BAKROL

2. TOPIC NAME: LAPLACE TRANSFORM
ELECTRICAL DEPARTMENT
STUDENT’S NAME ENROLLMENT NUMBER
ANUJ VERMA 141240109003
KARNVEER CHAUHAN 141240109011
MACHHI NIRAV 141240109012
MALEK MUAJHIDHUSEN 141240109013
DHARIYA PARMAR 141240109014
JAYEN PARMAR 141240109015
PARTH YADAV 141240109016
HARSH PATEL 14124010901
Guided by: ASHISH DHOKIYA and NIKHIL PARMAR

3. Definition of Laplace Transform
• Let f(t) be a given function of t defined for all
then the Laplace Transform ot f(t) denoted by L{f(t)}
or F(s) or is defined as
provided the integral exists, where s is a parameter real or
complex.
0t
)(sf )(s
dttfessFsftfL st
)()()()()}({
0



 

4. Laplace Transform of some
Elementary Functions
asif
a-s
1
)(
e.)e(
Definition-By:Proof
a-s
1
)L(e(2)
)0(,
s
1
1.)1(
Definition-By:Proof
s
1
L(1)(1)
0
)(
0
)(
0
atat
at
00
























 



as
e
dtedteL
s
s
e
dteL
tas
tasst
st
st

5. |a|s,
a-s
s
at]L[coshly,(5)Similar
|a|s,
a-s
a
11
2
1
)]()([
2
1
2
e
Lat)L(sinh
definitionBy
2
e
atcoshand
2
e
atsinhhave-We:Proof
a-s
a
at]L[sinh(4)
-as,
1
]L[e3)(
22
22
at
atat
22
at-

















 












asas
eLeL
e
ee
as
atat
at
atat

6. 0s,
as
s
at](7)L[cosand
as
a
at]L[sin
getweparts,imaginaryandrealEquating
as
a
i
as
s
as
ias
1
)L(e1
]e[]sin[cos
sincose
Formula]s[Euler'sincosethatknow-We:Proof
0s,
as
s
at]L[cosand
as
a
at]L[sin(6)
2222
222222
at
iat
iat
ix
2222































as
ias
LatiatL
atiat
xix


7.    n!1n0,1,2...n
n!
)(or
0,n-1n,
1
)(
1
ust,.)-L(:Proof
n!
or
1
)()8(
1
0
1
1
0
1)1(
1
0
0
11







































n
n
nx
n
n
nu
n
n
u
nstn
nn
n
S
tL
ndxxe
S
n
tL
duue
S
s
du
s
u
e
puttingdttet
SS
n
tL

8. Example

9. First Shifting Theorem
)(f]f(t)L[e,
)(f]f(t)L[e
)(f)(f
ra-swhere)(e
)(e
)(ef(t)]L[e
DefinitionByProof
)(f]f(t)L[ethen,(s)fL[f(t)]If
shifting-stheorem,shiftingFirst-Theorem
at-
at
0
rt-
0
a)t-(s-
0
st-at
at
asSimilarly
as
asr
dttf
dttf
dttfe
as
at















10. 22)-(s
2-s
)4cosL(e
2s
s
L(cosh2t)
)2coshL(e(2)
43)(s
3s
)4cosL(e
4s
s
L(cos4t)
)4cosL(e(1)
:
22
2t
22
2t
22
3t-
22
3t-










t
t
t
t
EXAMPLE

11. Second Shifting Theorem
a))L(f(tea))-u(tL(f(t)-Corr.
L(f(t))e
(s)fea))-u(ta)-L(f(t
then(s)fL(f(t))If
as-
as
as-






12.  
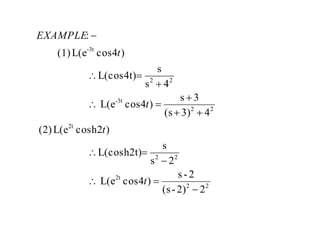
)(cos)2(
)2(cos)2()2(L
)()()(L
theroemshiftingsecondBy
(ii)L
33
1
}{.
}{)]2(L[e
2,ef(t)
)]2((i)L[e
22
1
22
2
1-
1-
22
2
1-
)3(2
)62(
362
)2(323t-
3t-
-3t
ttu
ttu
s
s
Ltu
s
se
atuatfsfe
s
se
s
e
s
e
eLee
eLetu
a
tuExample
s
as
s
s
s
ts
ts













































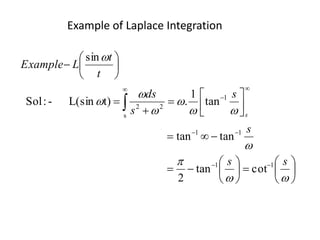
13. Differentiation & Integration of
Laplace Transform











0
n
n
nn
ds(s)f
t
f(t)
Lthen
,transformLaplacehas
t
f(t)
and(s)fL{f(t)}If
TransformsLaplaceofnIntegratio
1,2,3,...nwhere,(s)]f[
ds
d
(-1)f(t)]L[tthen(s)fL{f(t)}If
TranformLaplaceofationDifferenti

14. 3
2
2
2
2at2
at2
)(
2
)(
1
1
)1()e(-:Sol
)e(:
as
asds
d
asds
d
tL
tLExample




















Example of Laplace multiplication

15. 










































ss
s
s
s
ds
t
t
LExample
s
11
11
1
s
22
cottan
2
tantan
tan
1
.t)L(sin-:Sol
sin
Example of Laplace Integration

16. Evaluation of Integrals By Laplace
Transform






















1
)1()cos(
1
)(cos
cos)cos(
cos)(3
)()}({
cos-:Example
2
2
0
0
0
3
s
s
ds
d
ttL
s
s
tL
tdttettL
tttfs
dttfetfL
tdtte
st
st
t
25
2
100
8
)19(
19
cos
cos
)1(
1
)cos(
)1(
2)1(
1
2
0
3
0
22
2
22
22























tdtte
tdtte
s
s
ttL
s
ss
t
st

17. Laplace Transform of Derivatives &
Integral
 
f(u)du(s)f
1
LAlso
(s)f
1
f(u)duLthen(s),fL{f(t)}If
f(t)ofnintegratiotheoftransformLaplace
(0)(0)....ffs-f(0)s-(s)fs(t)}L{f
f(0)-(s)fsf(0)-sL{f(t)}(t)}fL{
and0f(t)elimprovidedexists,(t)}fL{then
continous,piecewiseis(t)fand0tallforcontinousisf(t)If
f(t)ofderivativetheoftransformLaplace
t
0
1-
t
0
1-n2-n1-nnn
st
t





















s
s

18. 22
2
22
3
22
2n
s
a
at)L(sin
at)L(sins
s
a-
a-at)L(sinssinat}L{-a
thisfroma(0)f0,f(0)Also
sinat-a(t)fandatcosa(t)fsinat thenf(t)Let:Sol
atsinoftransformlaplaceDeriveExample
a
a
a








)1(
1
)(
1
cos
cosf(u)-Here:Sol
cos
2
0
0


















ss
sf
s
uduL
u
uduLEg
t
t

19. Application to Differential Equations in
Laplace
04L(y))yL(
sidebothontranformLaplaceTaking
.
.
(0)y-(0)ys-y(0)s-Y(s)s(t))yL(
(0)y-sy(0)-Y(s)s(t))yL(
y(0)-sY(s)(t))yL(
Y(s)L(y(t))
6(0)y1y(0)04yy:
23
2





Example

20. tt
s
s
2sin
2
3
2cos
4s
6
4s
Y(s)
transformlaplaceinverseTaking
4s
6
Y(s)
06-s-4)Y(s)(s
04(Y(s))(0)y-sy(0)-Y(s)s
22
2
2
2











21. Laplace Transform of Periodic
Functions
 



p
0
st
0)(sf(t)dte
e-1
1
L{f(t)}
ispperiodwith
f(t)functionperiodiccontinouspiecewiseaoftransformlaplaceThe
0tallforf(t)p)f(t
if0)p(
periodithfunction wperiodicbetosaidisf(t)Afunction-Definition
ps-

22. 





























































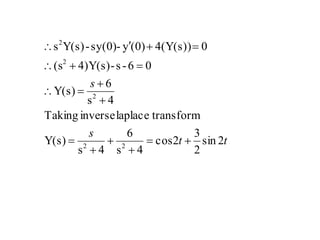
2w
sπ
hcot
ws
w
e
e
.
e1
e1
.
ws
w
e1
ws
w
.
e1
1
L[F(t)]
e1
ws
w
wcoswt)ssinwt(
ws
e
sinwtdteNow
tallforf(t)
w
π
tfand
w
π
t0forsinwtf(t)
0t|sinwt|f(t)
oftransformlaplacetheFind
22
2w
sπ
2w
sπ
w
sπ
w
sπ
22
w
sπ
22
w
sπ
w
sπ
22
2
w
π
0
w
π
0
22
st
st

23. Unit Step Function
s
1
L{u(t)}
0aif
e
s
1
s
e
(1)dte(0)dte
a)dt-u(tea)}-L{u(t
at1,
at0,a)-u(t
as-
a
st-
a
st-
a
0
st-
0
st-




















24. Express the following function in the terms of unit step
function and also find it’s Laplace transform
Example

25. Direct Delta function
1))((
))((
0
1
0lim
0







tL
eatL
tε, a
εat, a
ε
at, -a)δ(t
as
ε



26. Find the Laplace transform by direct delta method
Example

27. Inverse Laplace Transform
)()}({L
bydenotedisand(s)foftransformlaplaceinverse
thecalledisf(t)then(s),fL[f(t)]If-Definition
1-
tfsf 

Some standard Laplace inverse are:

28. Example of Laplace inverse
Example

29. =
=

30. Laplace inverse by partial differential form
2
1
2
1
12
1
)2(
2
1
)1(
1
2
1
C
than0s
2
1
B
than-2s
-1A
than-1s
2)1)(sc(s1)(s)B(s2)(s)A(s1
)2()1())(2)(1(
1
:
2)(s)1)(s(s
1
LExample
21
1
1




































tt
ee
sss
L
If
If
If
s
C
s
B
s
A
sss
LSolution

31. Convolution Theorem
g(t)*f(t)
g*fu)-g(tf(u)(s)}g(s)f{L
theng(t)(s)}g{Landf(t)(s)}f{LIf
t
0
1-
-1-1





32.  
)1(e
e
.e
.
)1(
1
)1(
1
.
1
)1(
1
n theoremconvolutioby
)(
1
1
(s)gand)(
1
(s)fhavewe:
)1(
1
:
t
0
t
0
t
0
2
1
1
2
1
2
2
1












































t
eue
dueu
dueu
ss
L
ss
L
ss
L
eL
s
tL
s
HereSol
ss
LExample
tuu
t
u
t
ut
t
Example of convolution theorem in Inverse Laplace

33. Example of convolution theorem

34. Thank You