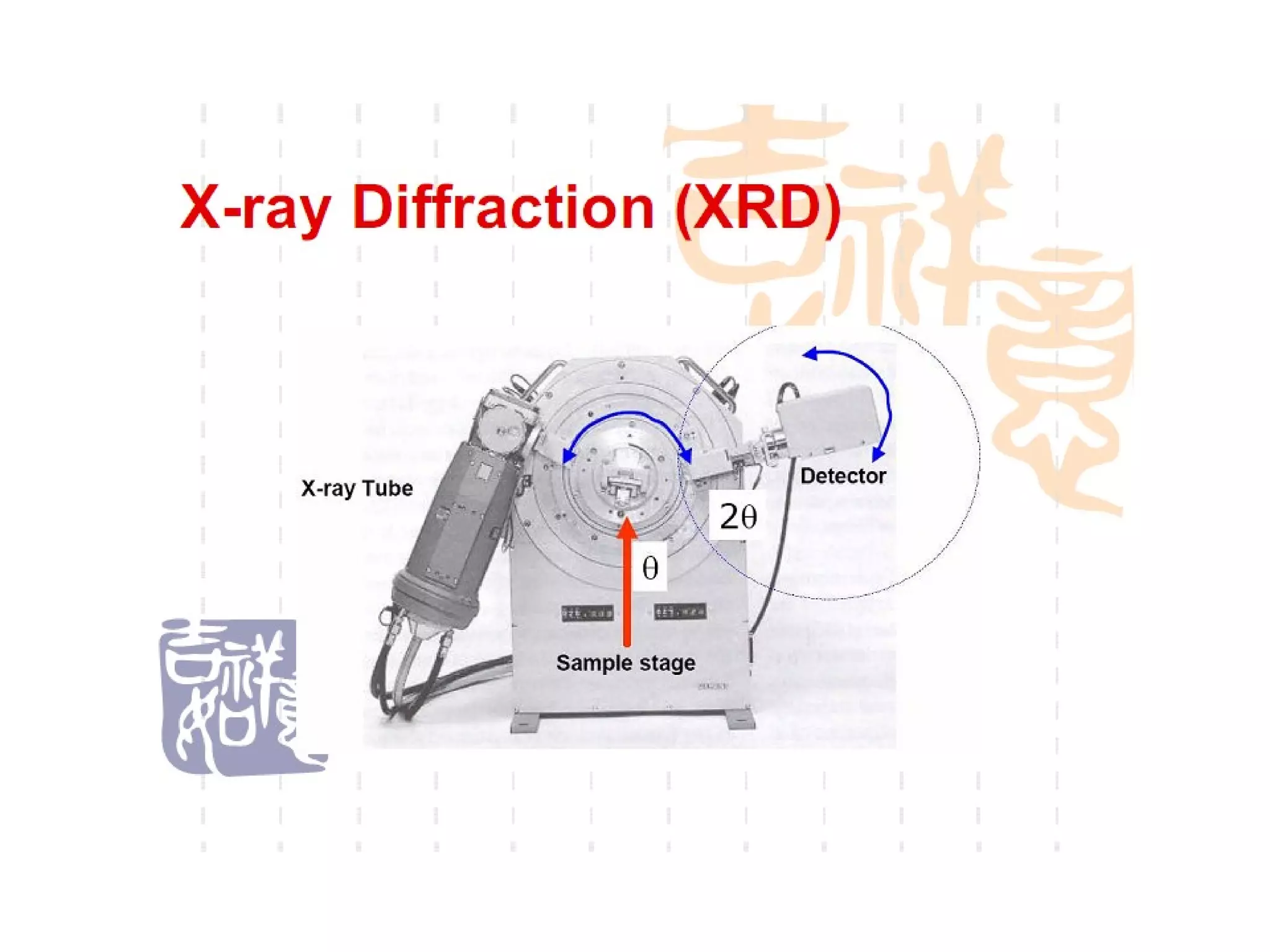
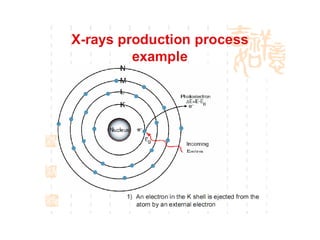
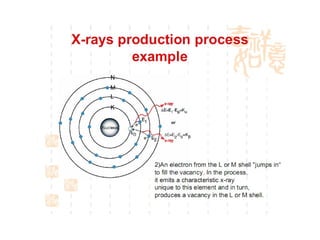
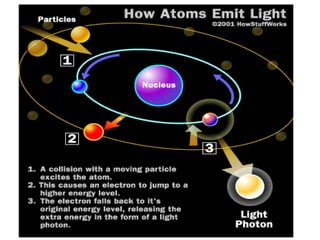
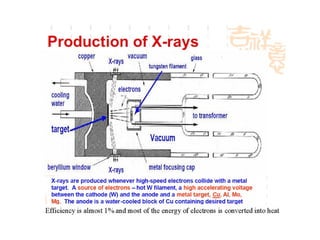
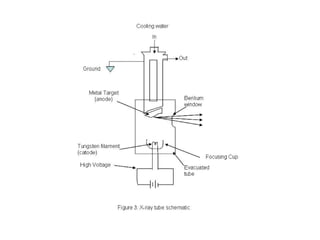
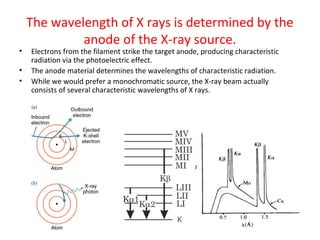
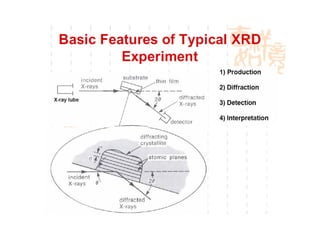
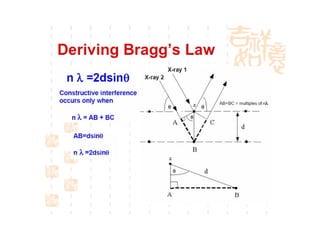
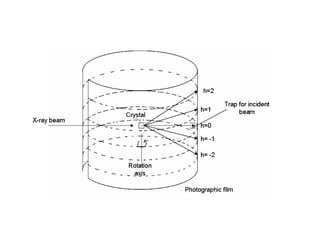
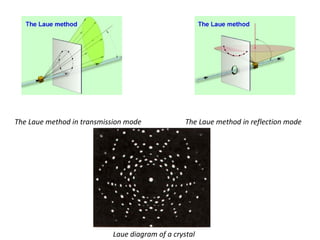
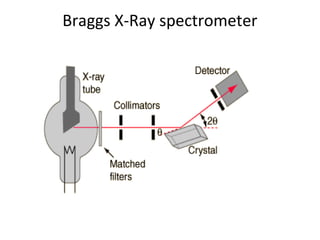
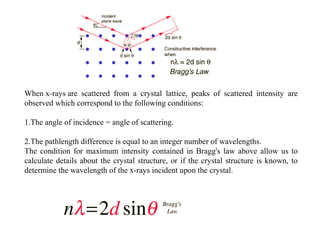
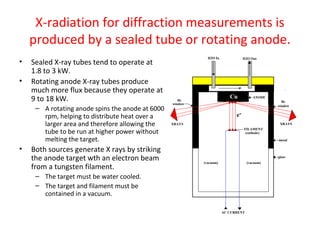
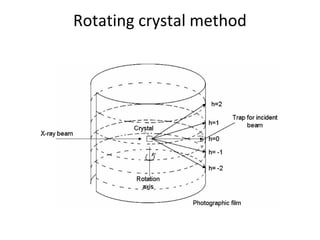
The document discusses the key components and functioning of a diffractometer used in X-ray crystallography. It describes the X-ray tube, optics, goniometer, sample holder, detector and how they are used to produce and analyze diffracted X-rays. It also explains Bragg's law which governs X-ray diffraction from crystal planes and is important for analyzing diffraction patterns. Different X-ray diffraction methods including Laue, rotating crystal and powder methods are also summarized.

11. Essential Parts of the Diffractometer
• X-ray Tube: the source of X Rays
• Incident-beam optics: condition the X-ray beam
before it hits the sample
• The goniometer: the platform that holds and
moves the sample, optics, detector, and/or tube
• The sample & sample holder
• Receiving-side optics: condition the X-ray beam
after it has encountered the sample
• Detector: count the number of X Rays scattered
by the sample

12. Instrumentation
• Production of X-Rays
• Collimator
• Monochromator
 Filter
 Crystal monochromator
• Detector
 Photographic methods
 Counter methods

13. The wavelength of X rays is determined by the
anode of the X-ray source.
• Electrons from the filament strike the target anode, producing characteristic
radiation via the photoelectric effect.
• The anode material determines the wavelengths of characteristic radiation.
• While we would prefer a monochromatic source, the X-ray beam actually
consists of several characteristic wavelengths of X rays.
K
L
M

18. Bragg’s law is a simplistic model to understand what
conditions are required for diffraction.
λ = 2d hkl sin θ θ θ
d hkl d hkl
• For parallel planes of atoms, with a space dhkl between the planes, constructive
interference only occurs when Bragg’s law is satisfied.
– In our diffractometers, the X-ray wavelength λ is fixed.
– Consequently, a family of planes produces a diffraction peak only at a specific angle θ.
– Additionally, the plane normal must be parallel to the diffraction vector
• Plane normal: the direction perpendicular to a plane of atoms
• Diffraction vector: the vector that bisects the angle between the incident and diffracted beam
• The space between diffracting planes of atoms determines peak positions.
• The peak intensity is determined by what atoms are in the diffracting plane.

23. XRD-Methods
• Laue photographic method
• Braggs X-Ray spectrometer
• Rotating crystal method
• Powder method

24. Laue photographic method
• In his first experiments, Max von Laue (Nobel Prize in Physics in 1914)
used continuous radiation (with all possible wavelengths) to impact on a
stationary crystal. With this procedure the crystal generates a set of
diffracted beams that show the internal symmetry of the crystal. In these
circumstances, and taking into account Bragg's Law, the experimental
constants are the interplanar spacings d and the crystal position referred
to the incident beam. The variables are the wavelength λ and the integer
number n:
n λ = 2 dhkl sin θnh,nk,nl
• Thus, the diffraction pattern will contain (for the same spacing d) the
diffracted beams corresponding to the first order of diffraction (n=1) of a
certain wavelength, the second order (n=2) of half the wavelength (λ/2),
the third order (n=3) with wavelength λ/3, etc. Therefore, the Laue
diagram is simply a stereographic projection of the crystal

26. The Laue method in transmission mode The Laue method in reflection mode
Laue diagram of a crystal

27. Braggs X-Ray spectrometer

28. When x-rays are scattered from a crystal lattice, peaks of scattered intensity are
observed which correspond to the following conditions:
1.The angle of incidence = angle of scattering.
2.The pathlength difference is equal to an integer number of wavelengths.
The condition for maximum intensity contained in Bragg's law above allow us to
calculate details about the crystal structure, or if the crystal structure is known, to
determine the wavelength of the x-rays incident upon the crystal.

29. X-radiation for diffraction measurements is
produced by a sealed tube or rotating anode.
H2O In H2O Out
• Sealed X-ray tubes tend to operate at
1.8 to 3 kW.
• Rotating anode X-ray tubes produce
much more flux because they operate at
9 to 18 kW. Be
Cu ANODE
Be
window
– A rotating anode spins the anode at 6000 window
rpm, helping to distribute heat over a e-
larger area and therefore allowing the XRAYS XRAYS
tube to be run at higher power without FILAMENT
(cathode)
melting the target. metal
• Both sources generate X rays by striking
the anode target wth an electron beam (vacuum) (vacuum)
glass
from a tungsten filament.
– The target must be water cooled.
– The target and filament must be
contained in a vacuum.
AC CURRENT

30. Rotating crystal method

31. Most of our powder diffractometers use the
Bragg-Brentano parafocusing geometry.
• A point detector and sample are
moved so that the detector is always
at 2θ and the sample surface is
always at θ to the incident X-ray
beam.
• In the parafocusing arrangement, the
incident- and diffracted-beam slits
move on a circle that is centered on
the sample. Divergent X rays from
the source hit the sample at different
points on its surface. During the
diffraction process the X rays are
refocused at the detector slit. F: the X-ray source
• This arrangement provides the best DS: the incident-beam divergence-limiting slit
SS: the Soller slit assembly
combination of intensity, peak shape, S: the sample
and angular resolution for the widest RS: the diffracted-beam receiving slit
number of samples. C: the monochromator crystal
AS: the anti-scatter slit

33. What is X-ray Powder Diffraction (XRD)
X-ray powder diffraction (XRD) is a rapid analytical
technique primarily used for phase identification of a
crystalline material and can provide information on unit
cell dimensions.
The analyzed material is finely ground, homogenized,
and average bulk composition is determined.

34. Fundamental Principles of X-ray Powder Diffraction (XRD)
 Max von Laue, in 1912, discovered that crystalline substances act
as three-dimensional diffraction gratings for X-ray wavelengths
similar to the spacing of planes in a crystal lattice.
 X-ray diffraction is now a common technique for the study of
crystal structures and atomic spacing.
 X-ray diffraction is based on constructive interference of
monochromatic X-rays and a crystalline sample.
 These X-rays are generated by a cathode ray tube, filtered to
produce monochromatic radiation, collimated to concentrate, and
directed toward the sample. The interaction of the incident rays
with the sample produces constructive interference (and a
diffracted ray) when conditions satisfy Bragg's Law (nλ=2d sin θ).

35.  This law relates the wavelength of electromagnetic radiation to
the diffraction angle and the lattice spacing in a crystalline sample.
 These diffracted X-rays are then detected, processed and counted.
 By scanning the sample through a range of 2θangles, all possible
diffraction directions of the lattice should be attained due to the
random orientation of the powdered material.
 Conversion of the diffraction peaks to d-spacings allows
identification of the mineral because each mineral has a set of
unique d-spacings. Typically, this is achieved by comparison of d-
spacings with standard reference patterns.

36.  All diffraction methods are based on generation of X-rays in an
X-ray tube. These X-rays are directed at the sample, and the
diffracted rays are collected.
 A key component of all diffraction is the angle between the
incident and diffracted rays. Powder and single crystal diffraction
vary in instrumentation beyond this.

37. Applications of XRD
• XRD is a nondestructive technique
• To identify crystalline phases and orientation
• To determine structural properties:
• Lattice parameters (10-4Å), strain, grain size, expitaxy,
phase composition, preferred orientation (Laue) order-
disorder transformation, thermal expansion
• To measure thickness of thin films and multi-layers
• To determine atomic arrangement
• Detection limits: ~3% in a two phase mixture; can be
~0.1% with synchrotron radiation
Spatial resolution: normally none

38. Applications
•X-ray powder diffraction is most widely used for the identification
of unknown crystalline materials (e.g. minerals, inorganic
compounds). Determination of unknown solids is critical to studies
in geology, environmental science, material science, engineering
and biology. Other applications include
• characterization of crystalline materials
• identification of fine-grained minerals such as clays and mixed
layer clays that are difficult to determine optically
• determination of unit cell dimensions measurement of sample
purity

39. With specialized techniques, XRD can be used to:
• determine crystal structures using Rietveld refinement
• determine of modal amounts of minerals (quantitative analysis)
• make textural measurements, such as the orientation of grains, in a
polycrystalline sample
• characterize thin films samples by:
 determining lattice mismatch between film and substrate and to inferring
stress and strain
 determining dislocation density and quality of the film by rocking curve
measurements
 measuring superlattices in multilayered epitaxial structures
 determining the thickness, roughness and density of the film using glancing
incidence X-ray reflectivity measurements

40. Strengths and Limitations of X-ray Powder Diffraction (XRD)?
Strengths
 Powerful and rapid (< 20 min) technique for identification of an
unknown mineral
 In most cases, it provides an unambiguous mineral determination
Minimal sample preparation is required
 XRD units are widely available
 Data interpretation is relatively straight forward

41. Limitations
 Homogeneous and single phase material is best for
identification of an unknown
 Must have access to a standard reference file of inorganic
compounds (d-spacings, hkls)
 Requires tenths of a gram of material which must be
ground into a powder
 For mixed materials, detection limit is ~ 2% of sample
For unit cell determinations, indexing of patterns for non-
isometric crystal systems is complicated
 Peak overlay may occur and worsens for high angle
'reflections'

42. SHIVA.PHARMACIST@GMAIL.COM
THANK
YOU