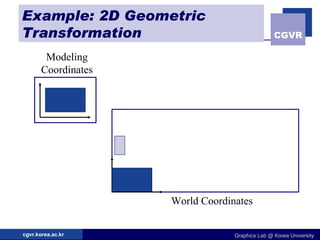
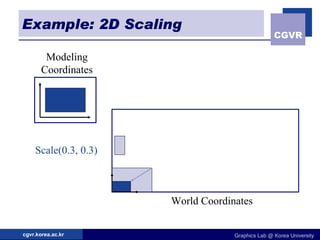
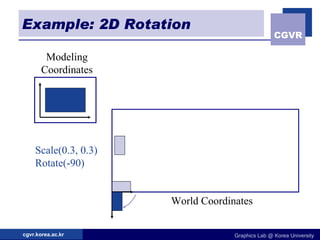
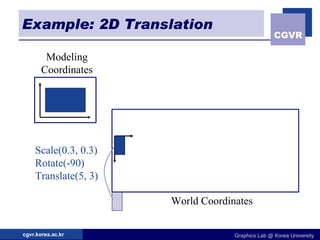
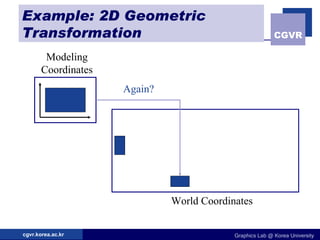
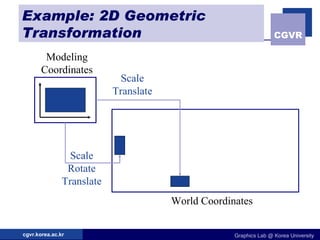
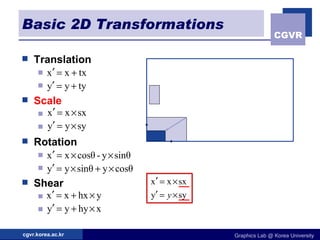
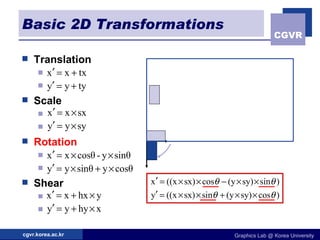
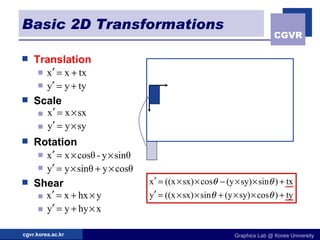
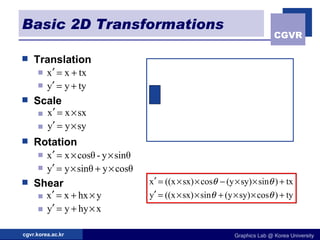
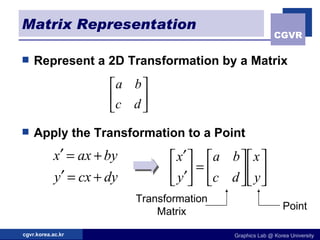
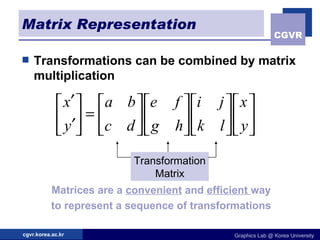
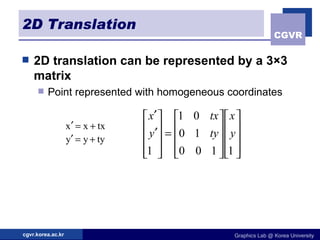
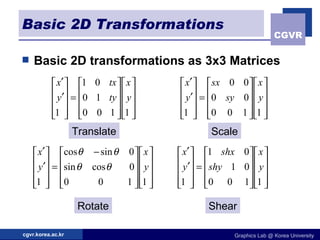
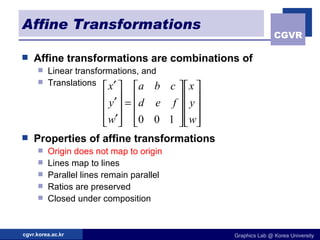
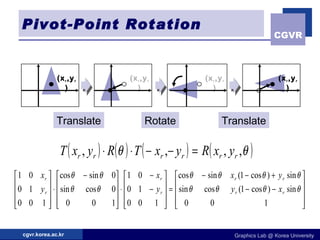
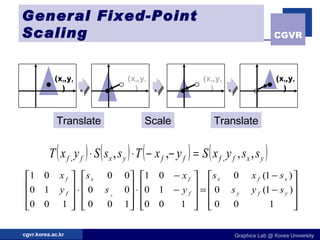
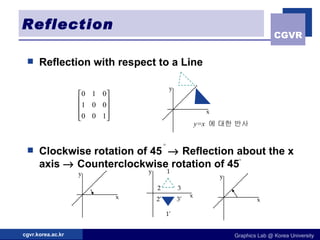
The document discusses 2D geometric transformations including translation, rotation, scaling, and their matrix representations. It explains that transformations can be combined through matrix multiplication and represented as sequences of transformations applied to modeling coordinates to obtain world coordinates. Basic transformations include translation, scaling, rotation, and shearing, which can be expressed as 3x3 matrices using homogeneous coordinates.

1. 2D Geometric Transformations 고려대학교 컴퓨터 그래픽스 연구실

2. Contents Definition & Motivation 2D Geometric Transformation Translation Rotation Scaling Matrix Representation Homogeneous Coordinates Matrix Composition Composite Transformations Pivot-Point Rotation General Fixed-Point Scaling Reflection and Shearing Transformations Between Coordinate Systems

3. Geometric Transformation Definition 물체의 좌표를 바꾸는 것 Translation, Rotation, Scaling Motivation – Why do we need geometric transformations in CG? As a viewing aid As a modeling tool As an image manipulation tool

4. Example: 2D Geometric Transformation Modeling Coordinates World Coordinates

5. Example: 2D Scaling Modeling Coordinates World Coordinates Scale(0.3, 0.3)

6. Example: 2D Rotation Modeling Coordinates Scale(0.3, 0.3) Rotate(-90) World Coordinates

7. Example: 2D Translation Modeling Coordinates Scale(0.3, 0.3) Rotate(-90) Translate(5, 3) World Coordinates

8. Example: 2D Geometric Transformation Modeling Coordinates World Coordinates Again?

9. Example: 2D Geometric Transformation Modeling Coordinates World Coordinates Scale Translate Scale Rotate Translate

10. Basic 2D Transformations Translation Scale Rotation Shear

11. Basic 2D Transformations Translation Scale Rotation Shear Transformations can be combined (with simple algebra)

12. Basic 2D Transformations Translation Scale Rotation Shear

13. Basic 2D Transformations Translation Scale Rotation Shear

14. Basic 2D Transformations Translation Scale Rotation Shear

15. Basic 2D Transformations Translation Scale Rotation Shear

16. Matrix Representation Represent a 2D Transformation by a Matrix Apply the Transformation to a Point Transformation Matrix Point

17. Matrix Representation Transformations can be combined by matrix multiplication Matrices are a convenient and efficient way to represent a sequence of transformations Transformation Matrix

18. 2×2 Matrices What types of transformations can be represented with a 2×2 matrix? 2D Identity 2D Scaling

19. 2×2 Matrices What types of transformations can be represented with a 2×2 matrix? 2D Rotation 2D Shearing

20. 2×2 Matrices What types of transformations can be represented with a 2×2 matrix? 2D Mirror over Y axis 2D Mirror over (0,0)

21. 2×2 Matrices What types of transformations can be represented with a 2×2 matrix? 2D Translation NO!! Only linear 2D transformations can be Represented with 2x2 matrix

22. 2D Translation 2D translation can be represented by a 3×3 matrix Point represented with homogeneous coordinates

23. Basic 2D Transformations Basic 2D transformations as 3x3 Matrices Translate Shear Scale Rotate

24. Homogeneous Coordinates Add a 3rd coordinate to every 2D point (x, y, w) represents a point at location (x/w, y/w) (x, y, 0) represents a point at infinity (0, 0, 0) Is not allowed 1 2 1 2 x y (2, 1, 1) or (4, 2, 2) or (6, 3, 3) Convenient Coordinate System to Represent Many Useful Transformations

25. Linear Transformations Linear transformations are combinations of … Scale Rotation Shear, and Mirror Properties of linear transformations Satisfies: Origin maps to origin Lines map to lines Parallel lines remain parallel Ratios are preserved Closed under composition

26. Affine Transformations Affine transformations are combinations of Linear transformations, and Translations Properties of affine transformations Origin does not map to origin Lines map to lines Parallel lines remain parallel Ratios are preserved Closed under composition

27. Projective Transformations Projective transformations… Affine transformations, and Projective warps Properties of projective transformations Origin does not map to origin Lines map to lines Parallel lines do not necessarily remain parallel Ratios are not preserved Closed under composition

28. Matrix Composition Transformations can be combined by matrix multiplication Efficiency with premultiplication Matrix multiplication is associative

29. Matrix Composition Rotate by  around arbitrary point (a,b) Scale by sx, sy around arbitrary point (a,b) (a,b) (a,b)

30. Pivot-Point Rotation Translate Rotate Translate (x r ,y r ) (x r ,y r ) (x r ,y r ) (x r ,y r )

31. General Fixed-Point Scaling Translate Scale Translate (x f ,y f ) (x f ,y f ) (x f ,y f ) (x f ,y f )

32. Reflection Reflection with respect to the axis • x 축에 대한 반사 • y 축에 대한 반사 • xy 축 ( 원점 ) 에 대한 y 축에 대한 반사 x 축에 대한 반사 원점에 대한 반사 x y 1 3 2 1’ 3’ 2’ x y 1 3 2 1’ 3’ 2 x y 3 1’ 3’ 2 1 2

33. Reflection Reflection with respect to a Line Clockwise rotation of 45  Reflection about the x axis  Counterclockwise rotation of 45 y=x 에 대한 반사 x y 1 3 2 1’ 3’ 2’ x y x y x y

34. Shear Converted to a parallelogram x’ = x + sh x · y, y’ = y Transformed to a shifted parallelogram (Y = Yref) x’ = x + sh x · ( y-y ref ), y’ = y x 축으로 밀림 ( Sh x =2 ) 선분에 대한 밀림 ( Sh x =1/2, y ref =-1 ) (0,0) (1,0) (1,1) (0,1) ( 0,0 ) ( 1,0 ) ( 1,1 ) (0,1) (0,0) (1,0) (3,1) (2,1) ( 1/2,0 ) ( 3/2,0 ) ( 2,1 ) ( 1,1 ) (0,-1) x y x y x y x y

35. Shear Transformed to a shifted parallelogram (X = Xref) x’ = x, y’ = sh y · ( x-x ref ) + y 선분에 대한 밀림 ( Sh y =1/2, x ref =-1 ) x y (-1,0) ( 0,0 ) ( 1,0 ) ( 1,1 ) ( 0,1 ) ( 0,1/2 ) ( 1,1 ) ( 1,2 ) ( 0,3/2 ) x y