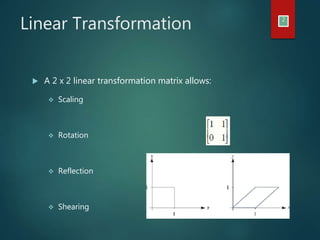
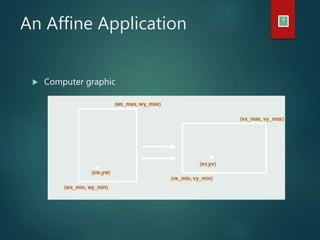
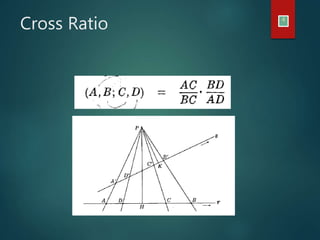
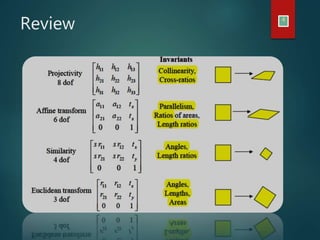
This document discusses different types of geometric transformations including linear transformations, affine transformations, and projective transformations. Linear transformations allow for scaling, rotation, reflection, and shearing using a 2x2 matrix. Affine transformations preserve parallel lines and proportional distances but not lengths and angles. Projective transformations describe how objects appear rather than how they are, distorting lengths, angles, and parallelism. Both affine and projective transformations are important applications in computer graphics and robot recognition.

1. Spatial
Transformations
BY : EHSAN HAMZEI - 810392121

2. Geometric transformations
 Geometric transformations will map points in one
space to points in another: (x',y',z') = f(x, y, z).
 These transformations can be very simple, such as
scaling each coordinate, or complex, such as nonlinear
twists and bends.
1

3. Linear Transformation
 A 2 x 2 linear transformation matrix allows:
 Scaling
 Rotation
 Reflection
 Shearing
2

4. Affine Transformation 3
 Definition:
 P(Px, Py) is transformed into Q(Qx , Qy ) as follows:
 Qx = aPx + cPy + Tx
 Qy = bPx + dPy + Ty

5. Affine Properties 4
 Preserves parallelism of lines, but not lengths and
angles.
 Lines are preserved.
 Proportional distances are preserved (Midpoints map
to midpoints).

6. An Affine Application 4
 Computer graphic

7. Projective Geometry 4
 Euclidean geometry describes shapes “as they are”.
 Projective geometry describes objects “as they
appear”. (Ex: Railroad…)
 Lengths, angles, parallelism become “distorted” when
we look at objects

8. Projective Transformation 4
 Definition:

9. Projective Properties 4
 With projective geometry, two lines always meet in a
single point, and two points always lie on a single line.
 Mapping from points in plane to points in plane
 3 aligned points are mapped to 3 aligned points
 Cross Ratio

10. Cross Ratio 4

11. A Projective Application 4
 Robot Recognition

12. Review 4

13. Thanks 26