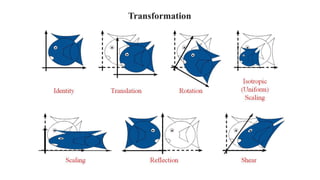
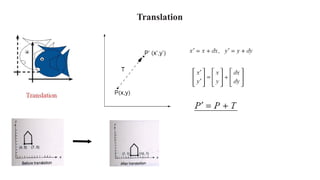
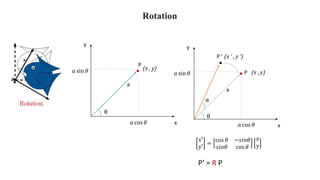
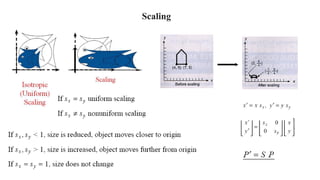
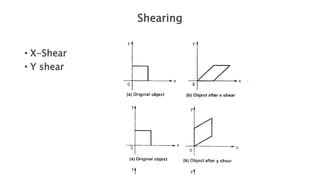
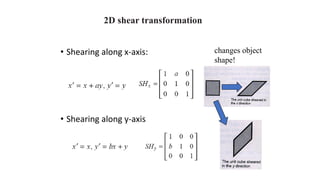
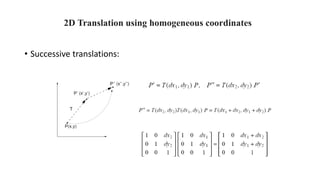
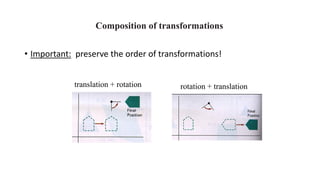
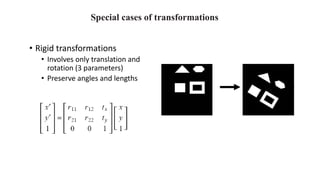
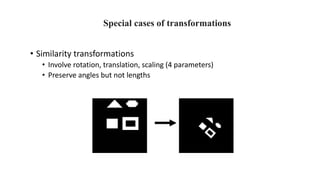
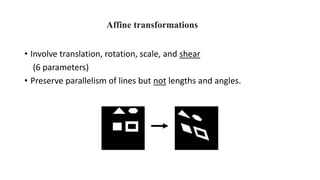
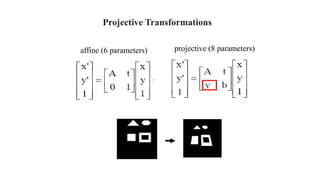
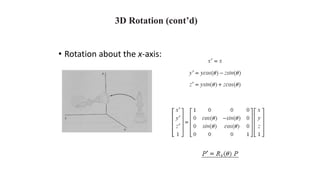
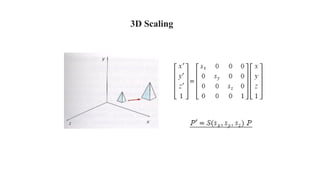
Geometric transformations change an object's position, orientation, or size. There are several types of 2D and 3D transformations, including translation, rotation, scaling, shearing, and their composition. Transformations can be represented using transformation matrices in homogeneous coordinates, where each point corresponds to a line. Special cases include rigid, similarity, and affine transformations that preserve certain properties like angles, lengths, and parallelism.

1. Transformations
Geometric transformations: Changing an object’s position (translation),
orientation (rotation) or size (scaling)

2. Geometry

3. Transformation

4. Translation

5. .
𝑎 cos 𝜃
𝑎 sin 𝜃 (x , y)
P
x
y
a
θ
.
.
𝑎 cos 𝜃
𝑎 sin 𝜃 (x , y)
P
x
y
a
θ
(x ‘ , y ‘)
P ‘
α
𝑥′
𝑦′
=
cos 𝜃 −𝑠𝑖𝑛𝜃
𝑠𝑖𝑛𝜃 cos 𝜃
𝑥
𝑦
P’ = R P
Rotation

6. Scaling

7. w=1
2D Translation using homogeneous coordinates

8. 2D Rotation using homogeneous coordinates
w=1

9. 2D Scaling using homogeneous coordinates
w=1

10. Shearing
• X-Shear
• Y shear

11. 2D shear transformation
• Shearing along x-axis:
• Shearing along y-axis
changes object
shape!

12. 2D Translation using homogeneous coordinates
• Successive translations:

13. 2D Scaling using homogeneous coordinates
• Successive scalings:

14. 2D Rotation using homogeneous coordinates
• Successive rotations:
or

15. Composition of transformations
• Important: preserve the order of transformations!
translation + rotation rotation + translation

18. General form of transformation matrix
• Representing a sequence of transformations as a single
transformation matrix is more efficient!
(only 4 multiplications and 4 additions)
translation
rotation, scale

19. Special cases of transformations
• Rigid transformations
• Involves only translation and
rotation (3 parameters)
• Preserve angles and lengths

20. Special cases of transformations
• Similarity transformations
• Involve rotation, translation, scaling (4 parameters)
• Preserve angles but not lengths

21. Affine transformations
• Involve translation, rotation, scale, and shear
(6 parameters)
• Preserve parallelism of lines but not lengths and angles.

22. Projective Transformations
affine (6 parameters) projective (8 parameters)

23. Homogeneous coordinates
• Add one more coordinate: (x,y,z) → (xh, yh, zh,w)
• Recover (x,y,z) by homogenizing (xh, yh, zh,w):
• In general, xh=xw, yh=yw, zh=zw
(x, y, z) → (xw, yw, zw, w)
• Each point (x, y, z) corresponds to a line in the 4D-space of
homogeneous coordinates.

24. Homogeneous coordinates
• (x, y) has multiple representations in homogeneous coordinates:
• w=1 (x,y) → (x,y,1)
• w=2 (x,y) → (2x,2y,2)
• All these points lie on a
line in the space of
homogeneous
coordinates !!

25. 3D Transformations

26. 3D Transformations
• Right-handed
(counter-clockwise rotations)
Positive rotation angles for right-handed systems:

27. 3D Translation

28. 3D Rotation
• Rotation about the z-axis:

29. 3D Rotation (cont’d)
• Rotation about the x-axis:

30. 3D Rotation (cont’d)
• Rotation about the y-axis

31. 3D Scaling

32. 1. Slides from CS485/685 Computer Vision, Dr. George Bebis
2. Saxena A, Sahay B. Computer aided engineering design. Springer
Science & Business Media; 2007 Dec 8.
References