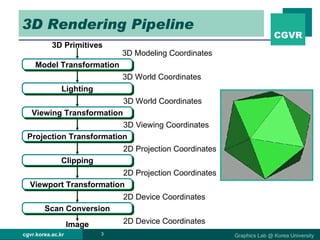
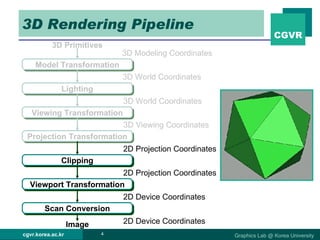
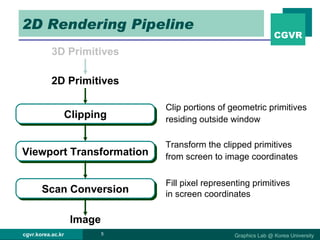
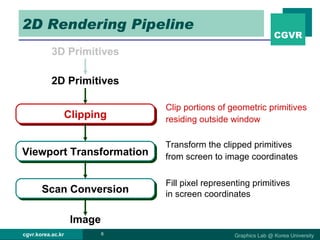
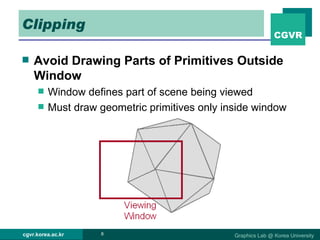
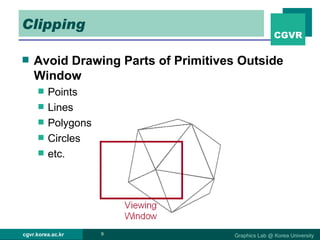
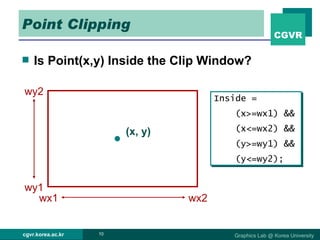
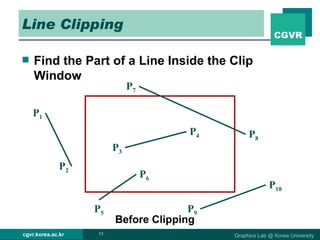
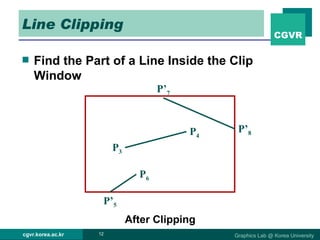
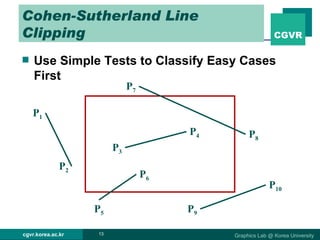
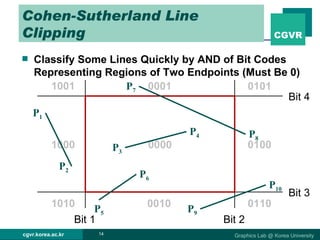
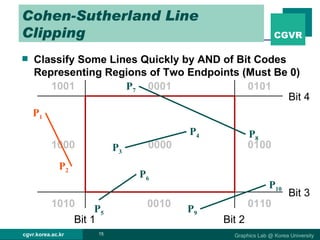
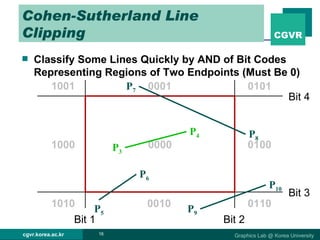
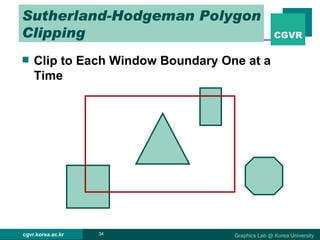
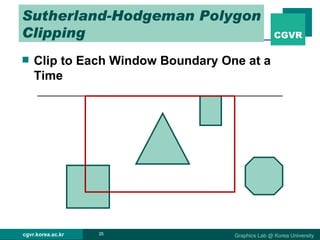
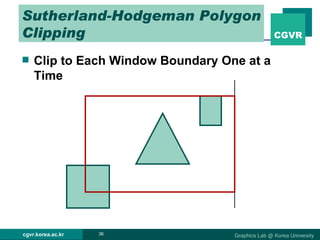
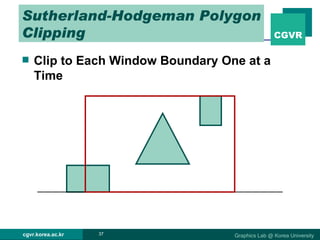
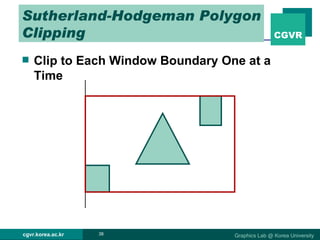
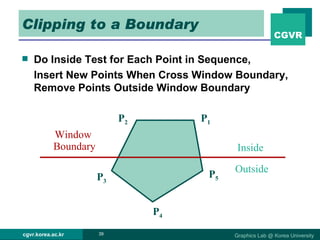
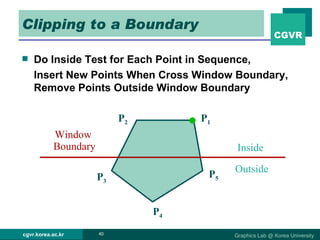
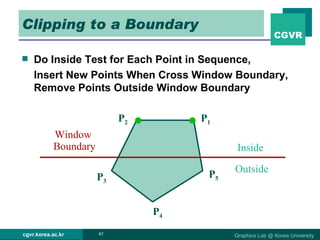
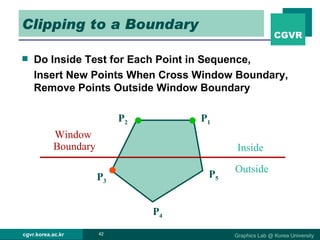
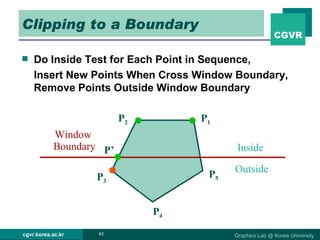
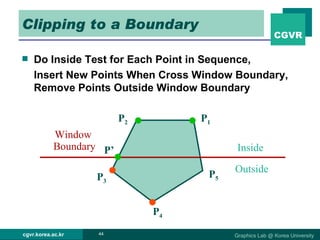
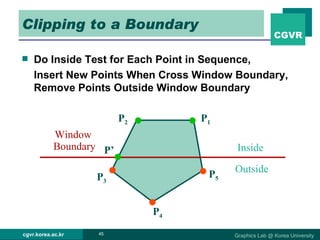
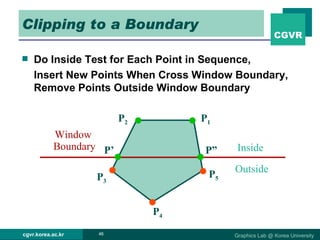
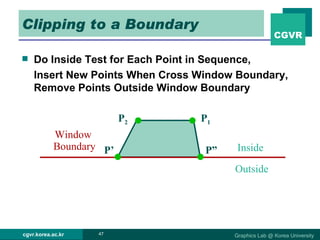
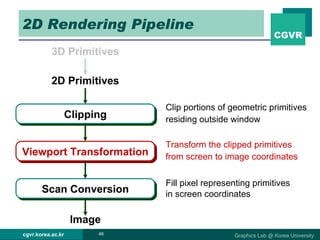
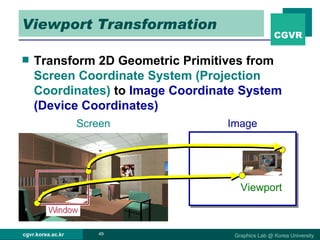
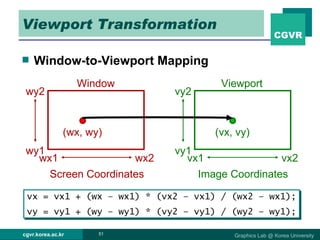
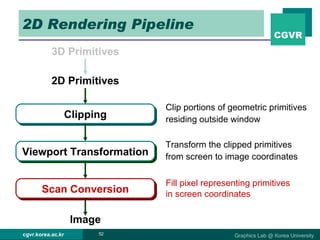
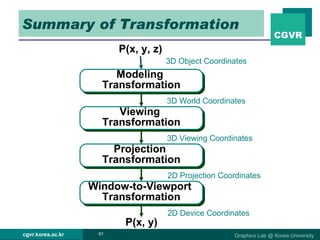
The document discusses 2D and 3D rendering pipelines. It describes techniques for clipping geometric primitives to a viewing window, including Cohen-Sutherland line clipping and Sutherland-Hodgeman polygon clipping. It also covers viewport transformation to map from screen to image coordinates, and scan conversion algorithms to determine which pixels are inside primitives like triangles and polygons.

1. 2D Viewing 고려대학교 컴퓨터 그래픽스 연구실

2. Contents 3D Rendering Pipeline 2D Rendering Pipeline Clipping Cohen-Sutherland Line Clipping Sutherland-Hodgeman Polygon Clipping Viewport Transformation Scan Conversion Summary of Transformation

3. 3D Rendering Pipeline Model Transformation Lighting Viewing Transformation Projection Transformation Clipping Viewport Transformation Scan Conversion 3D Primitives Image 3D Modeling Coordinates 3D World Coordinates 3D World Coordinates 3D Viewing Coordinates 2D Projection Coordinates 2D Projection Coordinates 2D Device Coordinates 2D Device Coordinates

4. 3D Rendering Pipeline Model Transformation Lighting Viewing Transformation Projection Transformation Clipping Viewport Transformation Scan Conversion 3D Primitives Image 3D Modeling Coordinates 3D World Coordinates 3D World Coordinates 3D Viewing Coordinates 2D Projection Coordinates 2D Projection Coordinates 2D Device Coordinates 2D Device Coordinates

5. 2D Rendering Pipeline 3D Primitives Clipping Viewport Transformation Scan Conversion Image Clip portions of geometric primitives residing outside window Transform the clipped primitives from screen to image coordinates Fill pixel representing primitives in screen coordinates 2D Primitives

6. 2D Rendering Pipeline 3D Primitives Clipping Viewport Transformation Scan Conversion Image Clip portions of geometric primitives residing outside window Transform the clipped primitives from screen to image coordinates Fill pixel representing primitives in screen coordinates 2D Primitives

7. Clipping Avoid Drawing Parts of Primitives Outside Window Window defines part of scene being viewed Must draw geometric primitives only inside window World Coordinates

8. Clipping Avoid Drawing Parts of Primitives Outside Window Window defines part of scene being viewed Must draw geometric primitives only inside window

9. Clipping Avoid Drawing Parts of Primitives Outside Window Points Lines Polygons Circles etc.

10. Point Clipping Is Point(x,y) Inside the Clip Window? (x, y) wx2 wx1 wy1 wy2 Inside = (x>=wx1) && (x<=wx2) && (y>=wy1) && (y<=wy2);

11. Line Clipping Find the Part of a Line Inside the Clip Window P 7 P 8 P 10 P 9 P 1 P 2 P 5 P 4 P 3 P 6 Before Clipping

12. Line Clipping Find the Part of a Line Inside the Clip Window After Clipping P 4 P 3 P 6 P’ 8 P’ 7 P’ 5

13. Cohen-Sutherland Line Clipping Use Simple Tests to Classify Easy Cases First P 7 P 8 P 10 P 9 P 1 P 2 P 5 P 4 P 3 P 6

14. Cohen-Sutherland Line Clipping Classify Some Lines Quickly by AND of Bit Codes Representing Regions of Two Endpoints (Must Be 0) P 10 P 5 P 6 P 9 0001 P 7 P 8 0101 0100 0110 0010 0000 1010 1000 P 1 P 2 1001 P 4 P 3 Bit 4 Bit 3 Bit 2 Bit 1

15. Cohen-Sutherland Line Clipping Classify Some Lines Quickly by AND of Bit Codes Representing Regions of Two Endpoints (Must Be 0) P 10 P 5 P 6 P 9 0001 P 7 P 8 0101 0100 0110 0010 0000 1010 1000 P 1 P 2 1001 P 4 P 3 Bit 4 Bit 3 Bit 2 Bit 1

16. Cohen-Sutherland Line Clipping Classify Some Lines Quickly by AND of Bit Codes Representing Regions of Two Endpoints (Must Be 0) P 10 P 5 P 6 P 9 0001 P 7 P 8 0101 0100 0110 0010 0000 1010 1000 1001 P 4 P 3 Bit 4 Bit 3 Bit 2 Bit 1

17. Cohen-Sutherland Line Clipping Compute Intersections with Window Boundary for Lines That Can’t be Classified Quickly P 10 P 5 P 6 P 9 0001 P 7 P 8 0101 0100 0110 0010 0000 1010 1000 1001 P 4 P 3 Bit 4 Bit 3 Bit 2 Bit 1

18. Cohen-Sutherland Line Clipping Compute Intersections with Window Boundary for Lines That Can’t be Classified Quickly P 10 P 5 P 6 P 9 0001 P 7 P 8 0101 0100 0110 0010 0000 1010 1000 1001 P 4 P 3 Bit 4 Bit 3 Bit 2 Bit 1

19. Cohen-Sutherland Line Clipping Compute Intersections with Window Boundary for Lines That Can’t be Classified Quickly P 10 P 6 P 9 0001 P 7 P 8 0101 0100 0110 0010 0000 1010 1000 1001 P 4 P 3 Bit 4 Bit 3 Bit 2 Bit 1 P’ 5

20. Cohen-Sutherland Line Clipping Compute Intersections with Window Boundary for Lines That Can’t be Classified Quickly P 10 P 6 P 9 0001 P 7 P 8 0101 0100 0110 0010 0000 1010 1000 1001 P 4 P 3 Bit 4 Bit 3 Bit 2 Bit 1 P’ 5

21. Cohen-Sutherland Line Clipping Compute Intersections with Window Boundary for Lines That Can’t be Classified Quickly P 10 P 6 P 9 0001 P 7 P 8 0101 0100 0110 0010 0000 1010 1000 1001 P 4 P 3 Bit 4 Bit 3 Bit 2 Bit 1 P’ 5

22. Cohen-Sutherland Line Clipping Compute Intersections with Window Boundary for Lines That Can’t be Classified Quickly P 10 P 6 P 9 0001 P 7 P 8 0101 0100 0110 0010 0000 1010 1000 1001 P 4 P 3 Bit 4 Bit 3 Bit 2 Bit 1 P’ 5

23. Cohen-Sutherland Line Clipping Compute Intersections with Window Boundary for Lines That Can’t be Classified Quickly P 10 P 6 P 9 0001 P 8 0101 0100 0110 0010 0000 1010 1000 1001 P 4 P 3 Bit 4 Bit 3 Bit 2 Bit 1 P’ 5 P’ 7

24. Cohen-Sutherland Line Clipping Compute Intersections with Window Boundary for Lines That Can’t be Classified Quickly P 10 P 6 P 9 0001 P 8 0101 0100 0110 0010 0000 1010 1000 1001 P 4 P 3 Bit 4 Bit 3 Bit 2 Bit 1 P’ 5 P’ 7

25. Cohen-Sutherland Line Clipping Compute Intersections with Window Boundary for Lines That Can’t be Classified Quickly P 10 P 6 P 9 0001 0101 0100 0110 0010 0000 1010 1000 1001 P 4 P 3 Bit 4 Bit 3 Bit 2 Bit 1 P’ 5 P’ 7 P’ 8

26. Cohen-Sutherland Line Clipping Compute Intersections with Window Boundary for Lines That Can’t be Classified Quickly P 10 P 6 P 9 0001 0101 0100 0110 0010 0000 1010 1000 1001 P 4 P 3 Bit 4 Bit 3 Bit 2 Bit 1 P’ 5 P’ 7 P’ 8

27. Cohen-Sutherland Line Clipping Compute Intersections with Window Boundary for Lines That Can’t be Classified Quickly P 10 P 6 P 9 0001 0101 0100 0110 0010 0000 1010 1000 1001 P 4 P 3 Bit 4 Bit 3 Bit 2 Bit 1 P’ 5 P’ 7 P’ 8

28. Cohen-Sutherland Line Clipping Compute Intersections with Window Boundary for Lines That Can’t be Classified Quickly P 10 P 6 P 9 0001 0101 0100 0110 0010 0000 1010 1000 1001 P 4 P 3 Bit 4 Bit 3 Bit 2 Bit 1 P’ 5 P’ 7 P’ 8

29. Cohen-Sutherland Line Clipping Compute Intersections with Window Boundary for Lines That Can’t be Classified Quickly P 10 P 6 0001 0101 0100 0110 0010 0000 1010 1000 1001 P 4 P 3 Bit 4 Bit 3 Bit 2 Bit 1 P’ 5 P’ 7 P’ 8 P’ 9

30. Cohen-Sutherland Line Clipping Compute Intersections with Window Boundary for Lines That Can’t be Classified Quickly P 6 0001 0101 0100 0110 0010 0000 1010 1000 1001 P 4 P 3 Bit 4 Bit 3 Bit 2 Bit 1 P’ 5 P’ 7 P’ 8 P 10 P’ 9

31. Cohen-Sutherland Line Clipping Compute Intersections with Window Boundary for Lines That Can’t be Classified Quickly P 6 0001 0101 0100 0110 0010 0000 1010 1000 1001 P 4 P 3 Bit 4 Bit 3 Bit 2 Bit 1 P’ 5 P’ 7 P’ 8

32. Polygon Clipping Find the Part of a Polygon Inside the Clip Window? Before Clipping

33. Polygon Clipping Find the Part of a Polygon Inside the Clip Window? After Clipping

34. Sutherland-Hodgeman Polygon Clipping Clip to Each Window Boundary One at a Time

35. Sutherland-Hodgeman Polygon Clipping Clip to Each Window Boundary One at a Time

36. Sutherland-Hodgeman Polygon Clipping Clip to Each Window Boundary One at a Time

37. Sutherland-Hodgeman Polygon Clipping Clip to Each Window Boundary One at a Time

38. Sutherland-Hodgeman Polygon Clipping Clip to Each Window Boundary One at a Time

39. Clipping to a Boundary Do Inside Test for Each Point in Sequence, Insert New Points When Cross Window Boundary, Remove Points Outside Window Boundary P 1 P 2 P 3 P 4 P 5 Inside Outside Window Boundary

40. Clipping to a Boundary Do Inside Test for Each Point in Sequence, Insert New Points When Cross Window Boundary, Remove Points Outside Window Boundary P 1 P 2 P 3 P 4 P 5 Inside Outside Window Boundary

41. Clipping to a Boundary Do Inside Test for Each Point in Sequence, Insert New Points When Cross Window Boundary, Remove Points Outside Window Boundary P 1 P 2 P 3 P 4 P 5 Inside Outside Window Boundary

42. Clipping to a Boundary Do Inside Test for Each Point in Sequence, Insert New Points When Cross Window Boundary, Remove Points Outside Window Boundary P 1 P 2 P 3 P 4 P 5 Inside Outside Window Boundary

43. Clipping to a Boundary Do Inside Test for Each Point in Sequence, Insert New Points When Cross Window Boundary, Remove Points Outside Window Boundary P 1 P 2 P 3 P 4 P 5 Inside Outside Window Boundary P’

44. Clipping to a Boundary Do Inside Test for Each Point in Sequence, Insert New Points When Cross Window Boundary, Remove Points Outside Window Boundary P 1 P 2 P 3 P 4 P 5 Inside Outside Window Boundary P’

45. Clipping to a Boundary Do Inside Test for Each Point in Sequence, Insert New Points When Cross Window Boundary, Remove Points Outside Window Boundary P 1 P 2 P 3 P 4 P 5 Inside Outside Window Boundary P’

46. Clipping to a Boundary Do Inside Test for Each Point in Sequence, Insert New Points When Cross Window Boundary, Remove Points Outside Window Boundary P 1 P 2 P 3 P 4 P 5 Inside Outside Window Boundary P’ P”

47. Clipping to a Boundary Do Inside Test for Each Point in Sequence, Insert New Points When Cross Window Boundary, Remove Points Outside Window Boundary P 1 P 2 Inside Outside Window Boundary P’ P”

48. 2D Rendering Pipeline 3D Primitives Clipping Viewport Transformation Scan Conversion Image Clip portions of geometric primitives residing outside window Transform the clipped primitives from screen to image coordinates Fill pixel representing primitives in screen coordinates 2D Primitives

49. Viewport Transformation Transform 2D Geometric Primitives from Screen Coordinate System (Projection Coordinates) to Image Coordinate System (Device Coordinates) Screen Image Viewport

50. Window vs. Viewport Window World-coordinate area selected for display What is to be viewed Viewport Area on the display device to which a window is mapped Where it is to be displayed

51. Viewport Transformation Window-to-Viewport Mapping (wx, wy) wx2 wx1 wy1 wy2 (vx, vy) vx2 vx1 vy1 vy2 Window Viewport Screen Coordinates Image Coordinates vx = vx1 + (wx – wx1) * (vx2 – vx1) / (wx2 – wx1); vy = vy1 + (wy – wy1) * (vy2 – vy1) / (wy2 – wy1);

52. 2D Rendering Pipeline 3D Primitives Clipping Viewport Transformation Scan Conversion Image Clip portions of geometric primitives residing outside window Transform the clipped primitives from screen to image coordinates Fill pixel representing primitives in screen coordinates 2D Primitives

53. Scan Conversion Definition Figure out which pixels to fill Example Filling the inside of a triangle P 1 P 2 P 3

54. Triangle Scan Conversion Simple Algorithm Color all pixels inside a triangle Inside triangle test A point is inside a triangle if it is in the positive halfspace of all three boundary lines L 1 L 2 L 3 P

55. Triangle Scan Conversion Triangle Sweep-Line Algorithm Take advantage of spatial coherence Compute which pixels are inside using horizontal spans Process horizontal spans in scan-line order Take advantage of edge linearity Use edge slopes to update coordinates incrementally dx dy

56. Polygon Scan Conversion Fill Pixels Inside a Polygon Triangle Quadrilateral Convex Star-Shaped Concave Self-Intersecting Holes

57. Inside Polygon Rule Need Better Test for Points Inside a Polygon “ Inside triangle test” works only for convex polygon Convex Polygon Concave Polygon L 1 L 2 L 3 L 4 L 5 L 1 L 2 L 3 L 4 L 5A L 5B

58. Inside Polygon Rule Odd-Parity Rule Any ray from P to infinity crosses odd number of edges Concave Self-Intersecting With Holes

59. Polygon Scan Conversion Polygon Line-Sweep Algorithm Incremental algorithm to find spans, and determine insideness with odd-parity rule Triangle Polygon

60. Polygon Scan Conversion Hardware Scan Conversion Convert everything into Triangles

61. Summary of Transformation P(x, y, z) Viewing Transformation Projection Transformation Window-to-Viewport Transformation P(x, y) Modeling Transformation 3D Object Coordinates 3D World Coordinates 3D Viewing Coordinates 2D Projection Coordinates 2D Device Coordinates