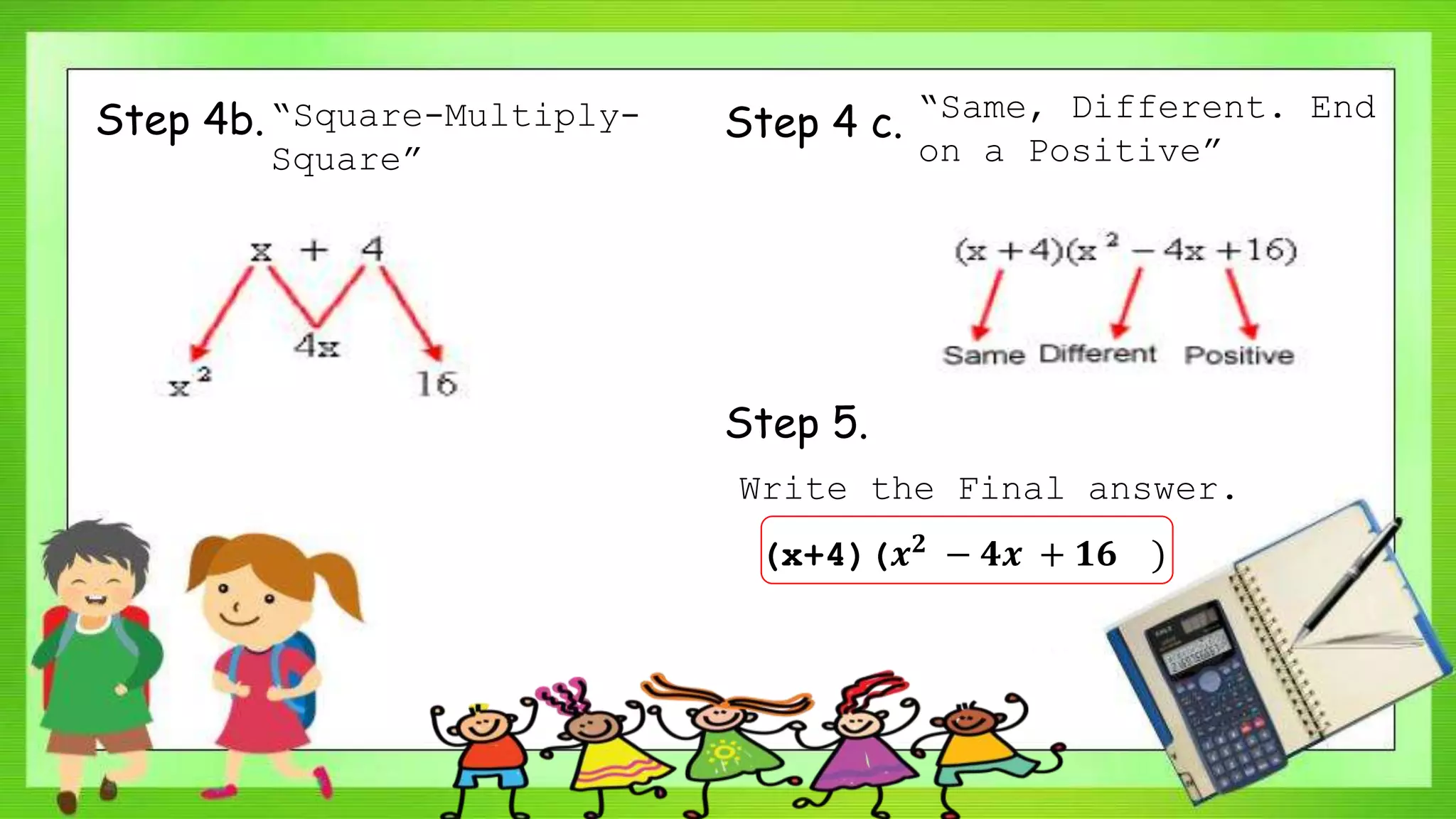
This document provides instructions on factoring the sum and difference of two cubes. It begins with objectives and a review of perfect cubes. It then explains that expressions like (x+4)(x^2 - 4x + 16) can be factored using the patterns for sum and difference of cubes. Two examples are worked through step-by-step to demonstrate factoring the sum and difference of two cubes using greatest common factors and rewriting the expression in terms of a and b cubes. The key steps and patterns are emphasized. It concludes with a reminder of what is important to remember from the lesson.

1. Factoring : Sum and Difference
of Two Cubes
Lorie Jane L. Letada
Module 1

2. Objectives
At the end of this lesson, you are expected to:
• identify which expression is sum
and difference of two cubes;
• factor the sum and difference
of two squares completely.

3. Review
Below is the list of the first 12 perfect cube numbers. Can
you give the answer of the last four?

4. What’s New

5. What is it
Recall that (𝒙+𝟒)(𝑥2− 𝟒𝒙+𝟏𝟔)= 𝑥3+𝟔𝟒 because of
the distributive property of multiplication. Now,
you are going to learn the reverse of this.
Your knowledge about the perfect cubes will
help you to identify the sum and difference of two
cubes.

6. To understand more on how to factor the sum and
difference of two cubes, here are the pattern, steps and
examples for you to follow. Factoring the Greatest Common
Factor is still important in this lesson.
Sum of Two Cubes:
𝒂 𝟑 + 𝒃 𝟑 =(𝒂+𝒃)(𝒂 𝟐 − 𝒂𝒃 + 𝒃 𝟐 )
Difference of Two Cubes:
𝒂 𝟑 - 𝒃 𝟑 =(𝒂-𝒃)(𝒂 𝟐 + 𝒂𝒃 + 𝒃 𝟐 )

7. Example 1 Factor 𝑥3
+ 64
Step 1. Step 2.
Check if the two terms
are perfect cubes. If
yes, proceed to the
next steps.
YES
Decide if the two terms have
anything in common, called the
greatest common factor or GCF.
If so, factor out the GCF. Do
not forget to include the GCF as
part of your final answer. In
this case, the two terms only
have a 1 in common which is of
no help.

8. Step 3. Rewrite the
original problem as
a sum/difference of
two perfect cubes.
𝑥3 + 64 = 𝑥 3 + (4)3
Step 4 a. “Write What You See”
If you disregard the
parenthesis and the
cubes in step 2, you
should see:
(𝑥 + 4 )

9. Step 4b.“Square-Multiply-
Square”
Step 4 c. “Same, Different. End
on a Positive”
Step 5.
Write the Final answer.
(x+4)(𝒙 𝟐 − 𝟒𝒙 + 𝟏𝟔 )

10. Example 2 Factor 2𝑥3
− 16
Step 1. Step 2.
Check if the two terms
are perfect cubes. If
yes, proceed to the
next steps.
YES
Decide if the two terms have
anything in common, called the
greatest common factor or GCF.
If so, factor out the GCF. Do
not forget to include the GCF as
part of your final answer. In
this case, the two terms only
have a 1 in common which is of
no help.
GCF: 2
2 (𝑥3
− 8 )

11. Step 3. Rewrite the
original problem as
a sum/difference of
two perfect cubes.
2𝑥3 − 16 = 2 [ 𝑥 3 − 2 3 ]
Step 4 a. “Write What You See”
If you disregard the
parenthesis and the
cubes in step 2, you
should see:
2 (𝑥 − 2 )

12. Step 4b.“Square-Multiply-
Square”
Step 4 c. “Same, Different. End
on a Positive”
Step 5.
Write the Final answer.
2(x-2)(𝒙 𝟐 + 𝟐𝒙 + 𝟒 )

13. Activity 1.3 Color Me

14. What I need to remember
The sum and difference of two cubes can only be
factored if the given expression is a binomial and
the two terms have perfect cubes.

15. Mathematics is not about
numbers, equations,
computations, or
algorithms: it is about
understanding. –William
Paul Thurston