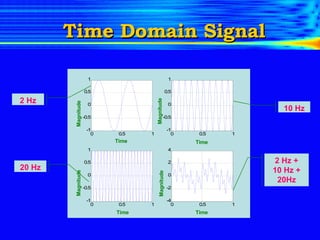
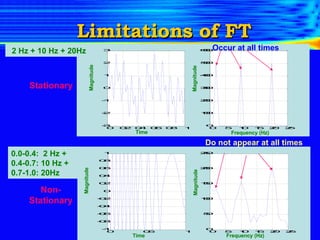
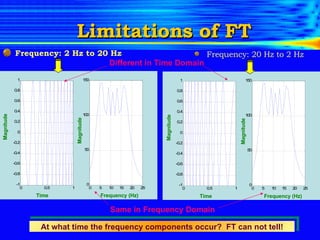
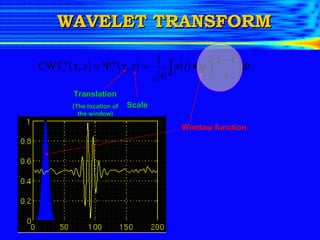
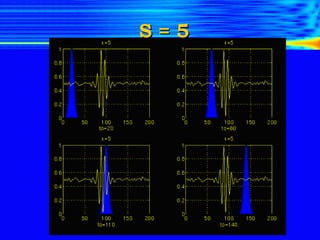
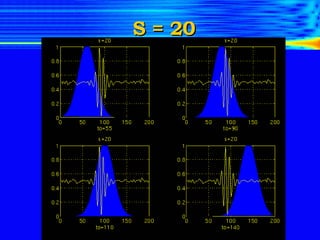
The document introduces the limitations of Fourier transforms for analyzing non-stationary signals and discusses how wavelet transforms provide a solution. Fourier transforms can only provide frequency content over the entire signal duration and cannot localize this content in time. Wavelet transforms overcome this by analyzing the signal with translated and scaled versions of an analyzing wavelet, allowing time-frequency localization. This provides a time-frequency representation of non-stationary signals and indicates when different frequency components occur.

1. Introduction to Wavelet Transform

2. TABLE OF CONTENT Frequency analysis Limitations of Fourier Transform Wavelet Transform Summary

3. Time Domain Signal 10 Hz 2 Hz 20 Hz 2 Hz + 10 Hz + 20Hz Time Time Time Time Magnitude Magnitude Magnitude Magnitude

4. FREQUENCY ANALYSIS Frequency Spectrum the frequency components (spectral components) of that signal Show what frequencies exists in the signal Fourier Transform (FT) Most popular way to find the frequency content Tells how much of each frequency exists in a signal

5. Limitations of FT Stationary Signal Signals with frequency content unchanged in time All frequency components exist at all times Fourier transform is good at stationary signals. Non-stationary Signal Frequency changes in time Fourier transform is not good at representing non-stationary signals.

6. Limitations of FT Occur at all times Do not appear at all times Time Magnitude Magnitude Frequency (Hz) 2 Hz + 10 Hz + 20Hz Stationary Time Magnitude Magnitude Frequency (Hz) Non-Stationary 0.0-0.4: 2 Hz + 0.4-0.7: 10 Hz + 0.7-1.0: 20Hz

7. Frequency: 2 Hz to 20 Hz Limitations of FT Same in Frequency Domain Frequency: 20 Hz to 2 Hz At what time the frequency components occur? FT can not tell! Time Magnitude Magnitude Frequency (Hz) Time Magnitude Magnitude Frequency (Hz) Different in Time Domain

8. FT Only Gives what Frequency Components Exist in the Signal Time-frequency Representation of the Signal is Needed Limitations of FT Many Signals in our daily life are Non-stationary. (We need to know whether and also when an incident was happened.)

9. Solutions = Wavelet Transform

10. WAVELET TRANSFORM Translation (The location of the window) Scale Window function

11. SCALE and Translation Large scale: Large window size, low frequency components. Small scale: Small window size, high frequency components. Translation: Shift the window to different location of the signal

12. S = 5

13. S = 20

14. COMPUTATION OF CWT Step 1: The wavelet is placed at the beginning of the signal, and set s=1 (the most compressed wavelet); Step 2: The wavelet function at scale “1” is multiplied by the signal, and integrated over all times; then multiplied by ; Step 3: Shift the wavelet to t = , and get the transform value at t = and s =1; Step 4: Repeat the procedure until the wavelet reaches the end of the signal; Step 5: Scale s is increased by a sufficiently small value, the above procedure is repeated for all s; Step 6: Each computation for a given s fills the single row of the time-scale plane; Step 7: CWT is obtained if all s are calculated.

15. Summary Frequency analysis can obtain frequency content of the signal. Fourier transform cannot deal with non-stationary signal. Wavelet transform can give a good time-frequency representation of the non-stationary signal.

16. End