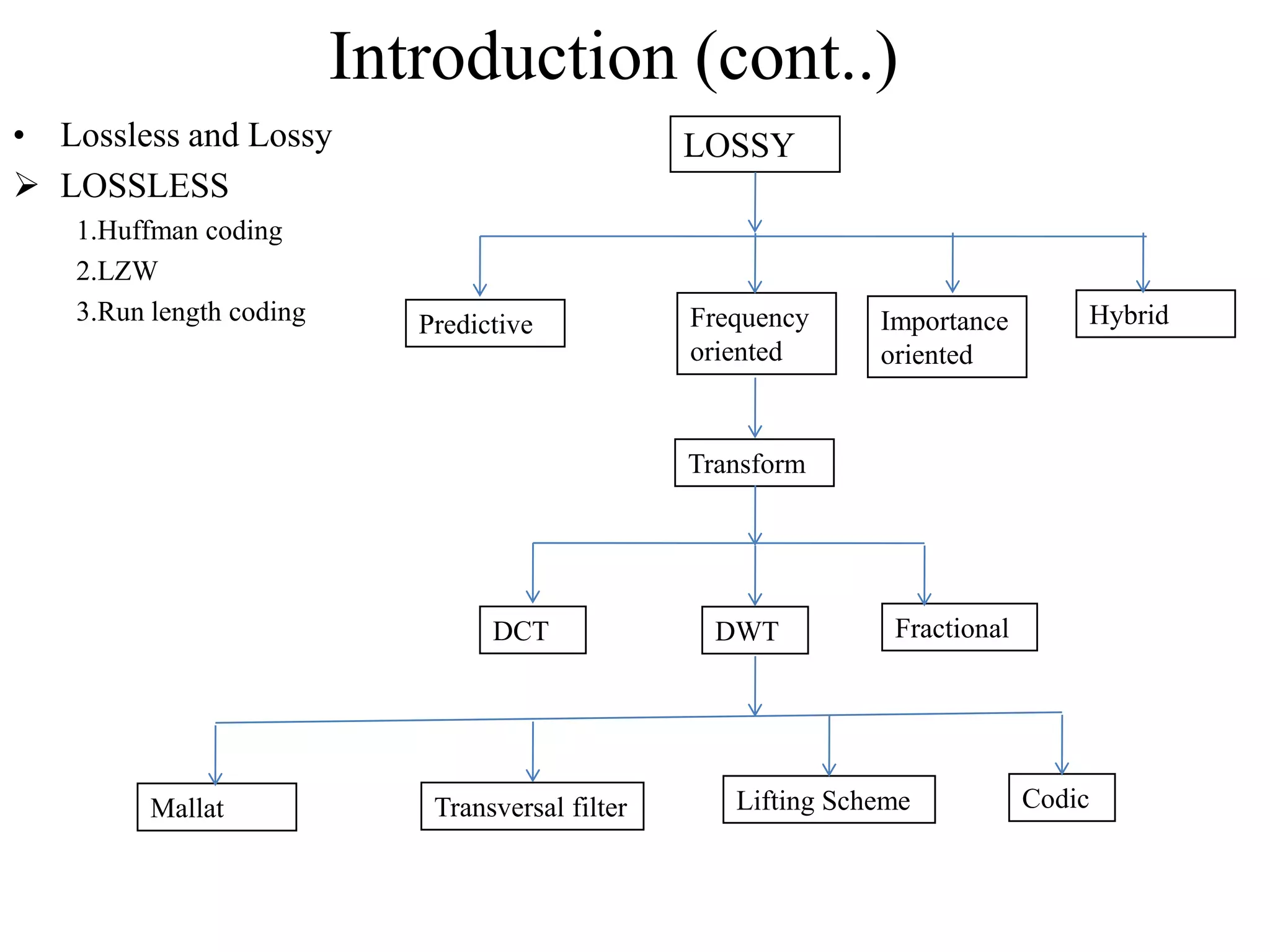
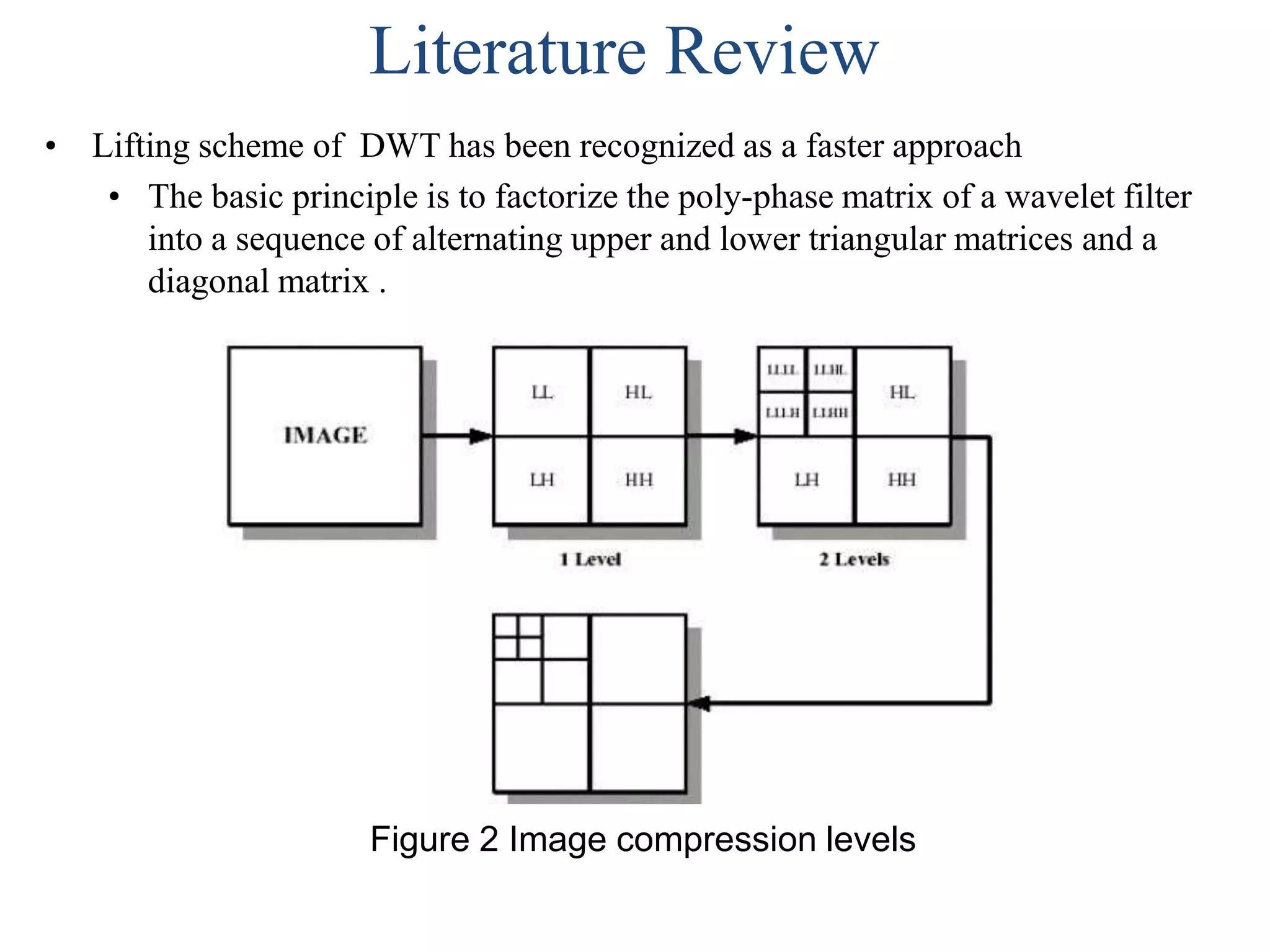
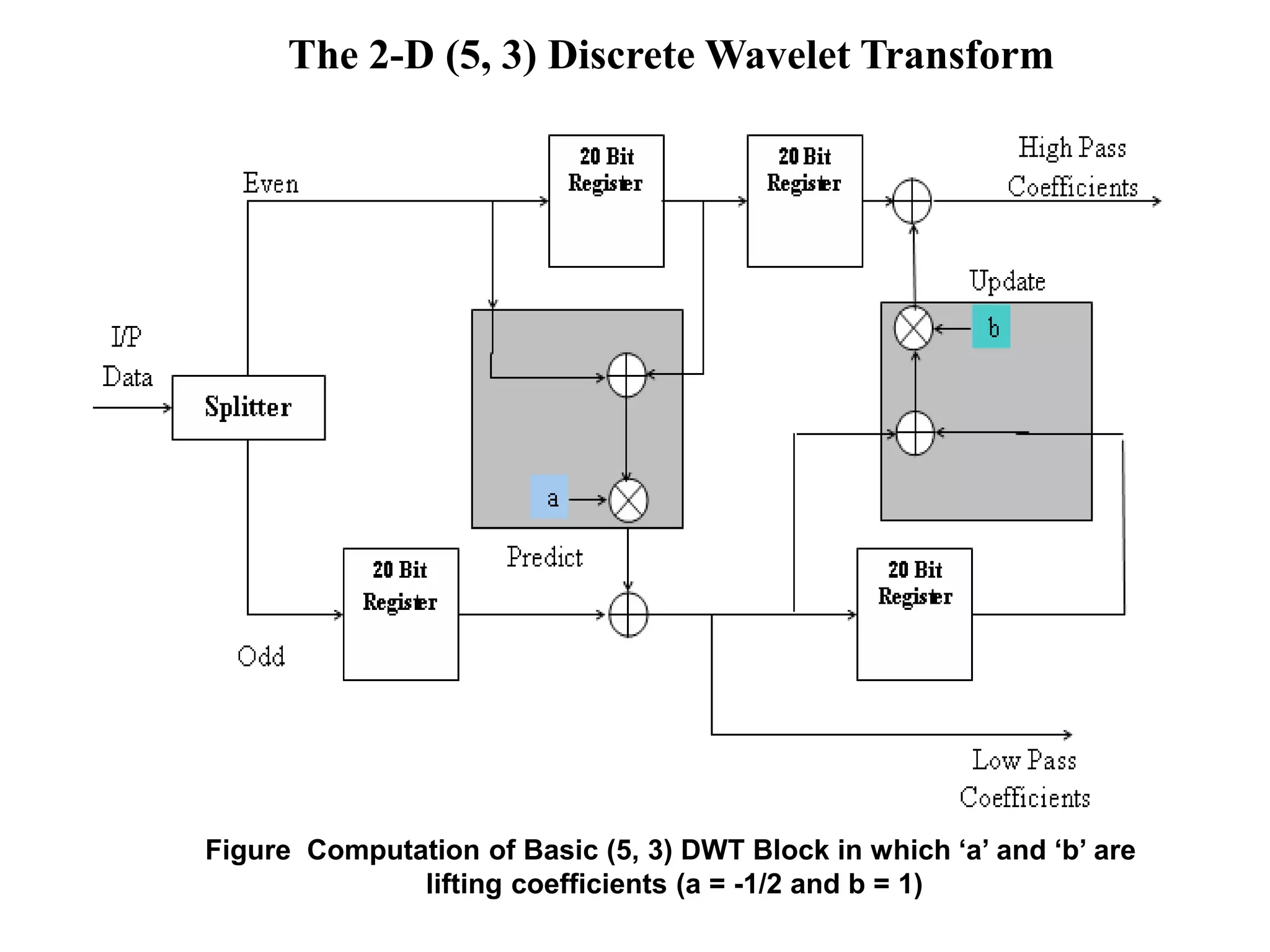
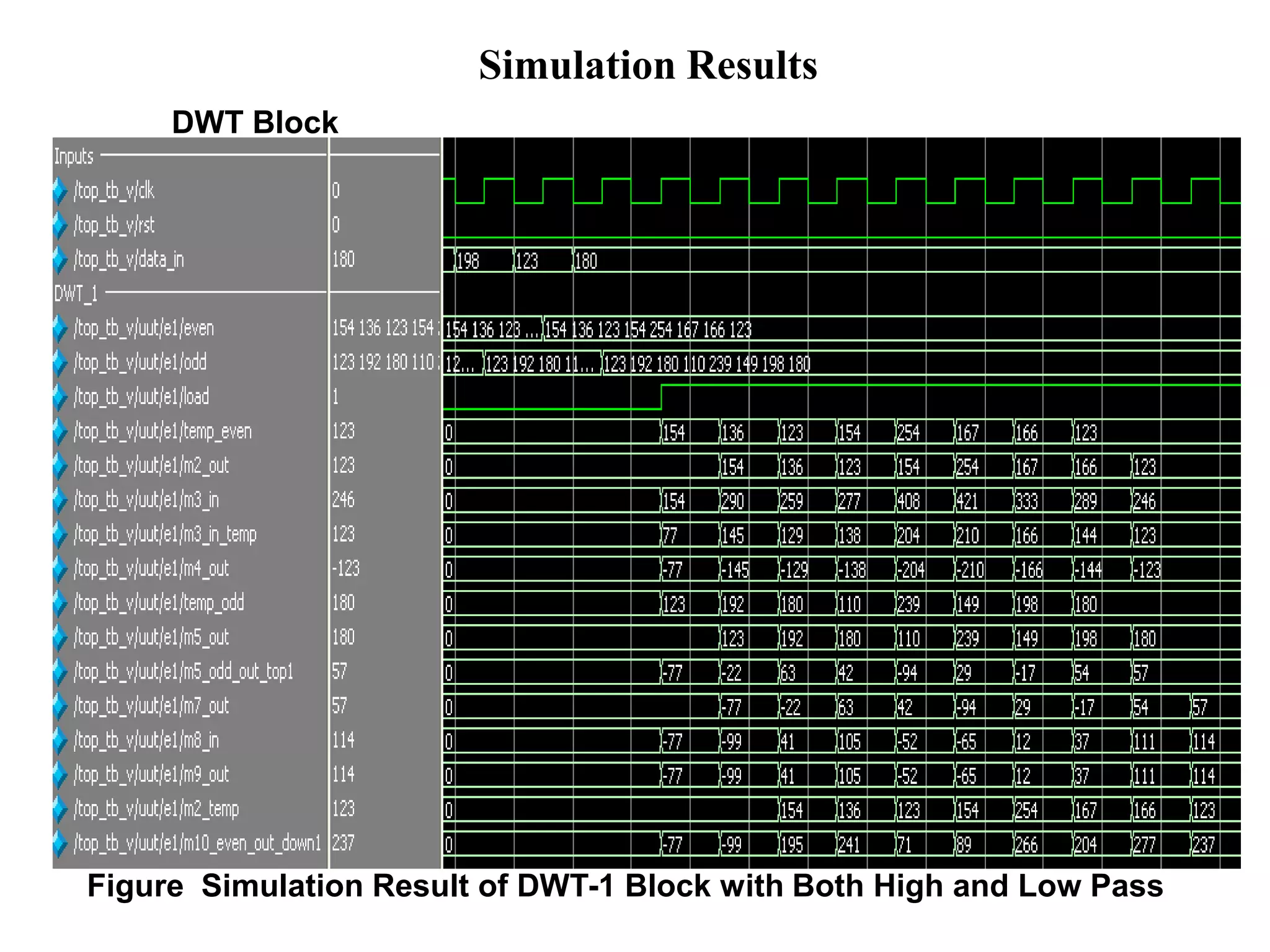
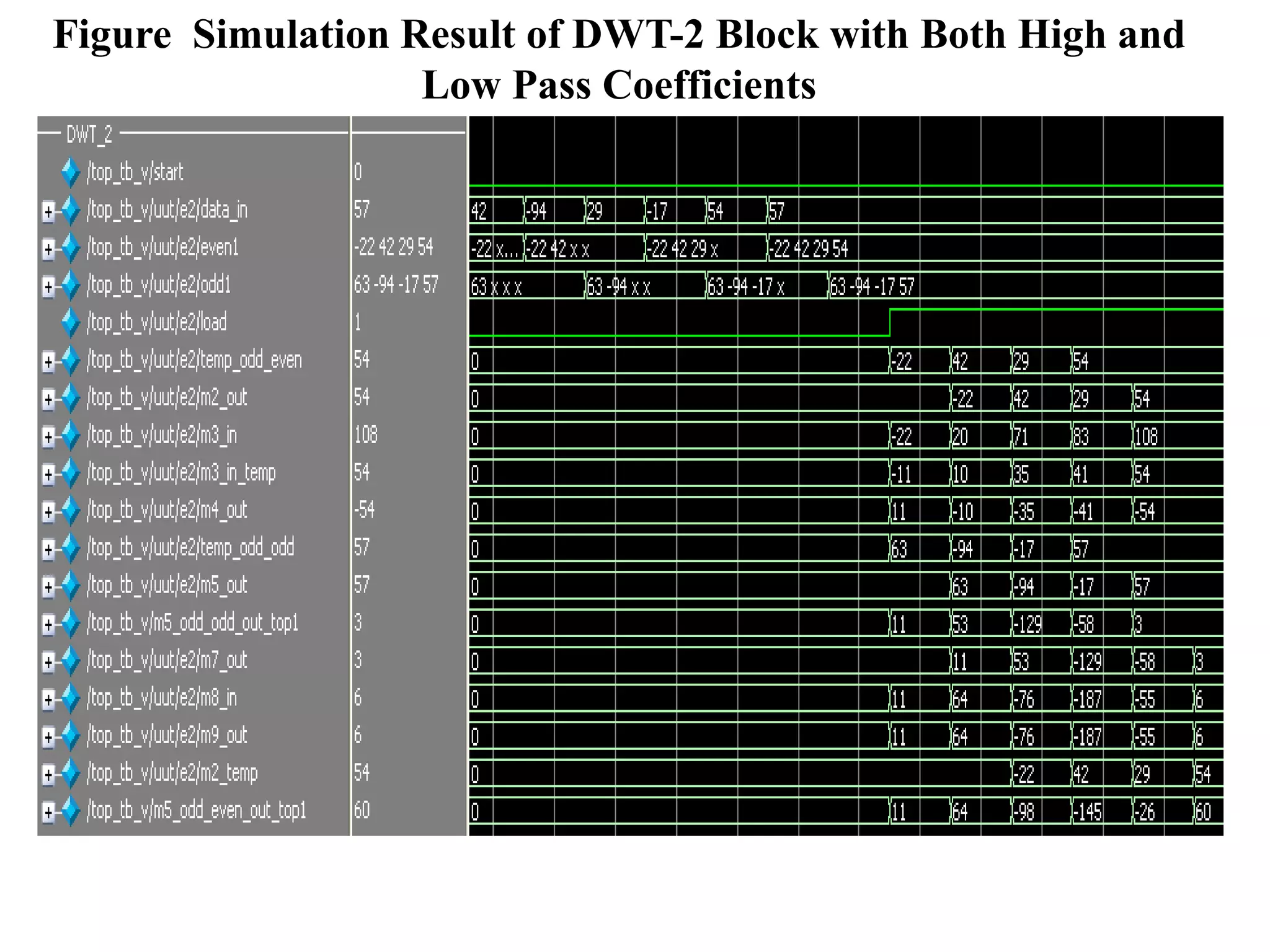
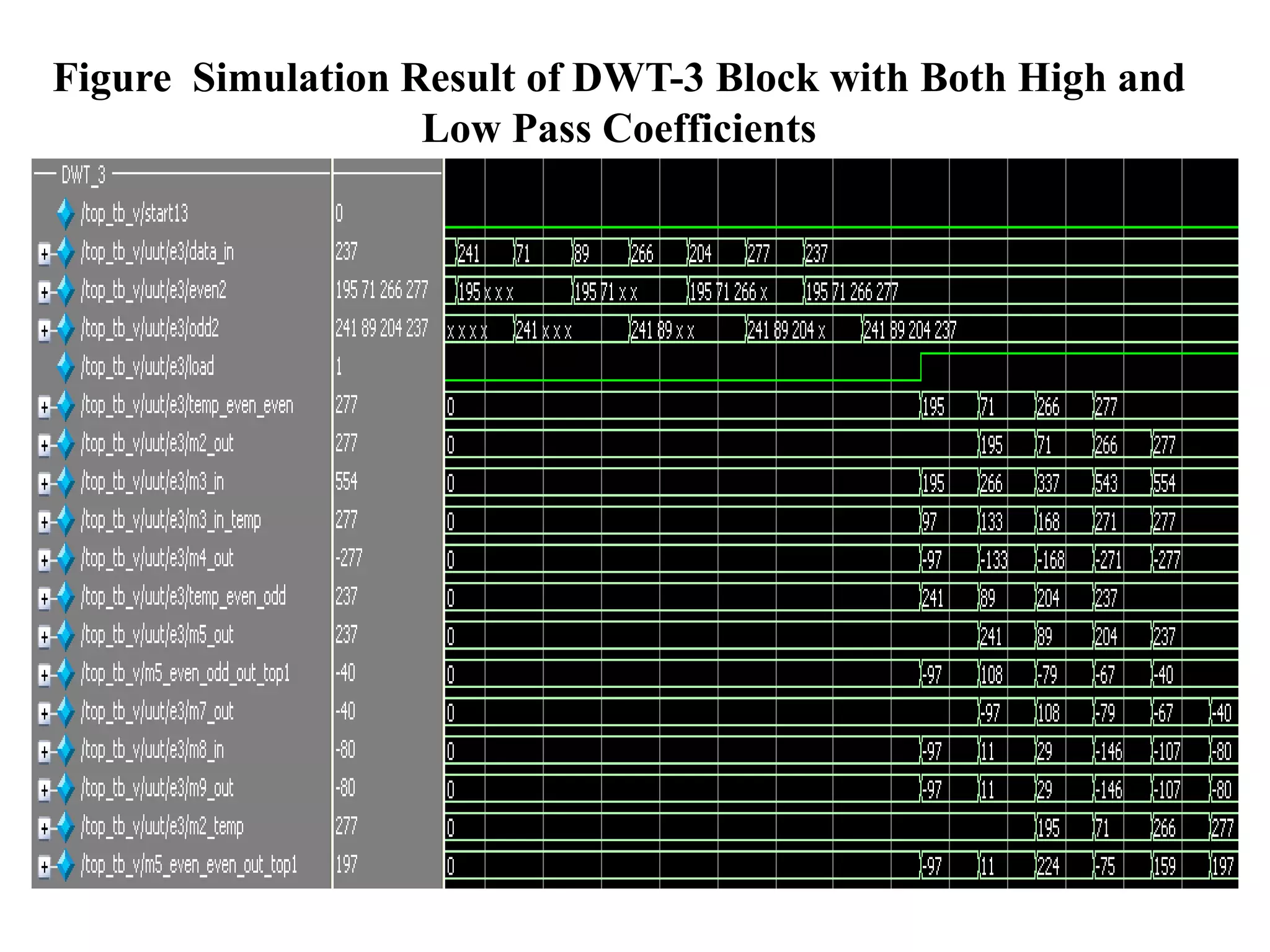
This document summarizes a student project on implementing lossless discrete wavelet transform (DWT) and inverse discrete wavelet transform (IDWT). It provides an overview of the project, which includes introducing DWT, reviewing literature on lifting schemes for faster DWT computation, and simulating a 2D (5,3) DWT. The results show DWT blocks decomposing signals into high and low pass coefficients. Applications mentioned are in medical imaging, signal denoising, data compression and image processing. The conclusion discusses the need for lossless transforms in medical imaging. Future work could extend this to higher level transforms and applications like compression and watermarking.

1. J.B.INSTITUTE OF ENGINEERING AND TECHNOLOGY
Design and Implementation of Lossless DWT/IDWT (Discrete
Wavelet Transform & Inverse Discrete Wavelet Transform)
BY
PIYUSH SETHIA
08671A0463
(E.C.E)
INTERNAL GUIDE H.O.D
SYED MOHD ALI S. P. VENU MADHAVA RAO

2. OVERVIEW
1. Introduction
2. Literature review
3. Discrete wavelet transform
4. Lifting scheme
5. Simulation results
6. Conclusion
7. Future scope

3. Introduction
Why Discrete wavelet transform?
Inherent multi-resolution nature,
wavelet-coding schemes
for applications where scalability and tolerable
degradation are important.

4. What is wavelets?
• Wavelet transform decomposes a signal into a
set of basis functions. These basis functions
are called wavelets
What is Discrete wavelet transform?
• Discrete wavelet transform (DWT), which
transforms a discrete time signal to a discrete
wavelet representation.

5. Introduction (cont..)
There are two types of compressions
1.Lossless
Digitally identical to the original image.
Only achieve a modest amount of
compression
2.Lossy
Discards components of the signal that are
known to be redundant. Signal is therefore
changed from input

6. Introduction (cont..)
• Lossless and Lossy LOSSY
 LOSSLESS
1.Huffman coding
2.LZW
3.Run length coding Predictive Frequency Importance Hybrid
oriented oriented
Transform
DCT DWT Fractional
Mallat Transversal filter Lifting Scheme Codic

7. Literature Review
• Lifting scheme of DWT has been recognized as a faster approach
• The basic principle is to factorize the poly-phase matrix of a wavelet filter
into a sequence of alternating upper and lower triangular matrices and a
diagonal matrix .
Figure 2 Image compression levels

8. Literature Review (cont..)
• 2-D DWT for Image
Figure 3 Image compression and decoded image

9. 2-D (5, 3) DWT – Lossless Transformation
The even and odd coefficient equations for (5, 3) Inverse Integer Wavelet
Transform are

10. The 2-D (5, 3) Discrete Wavelet Transform
Figure Computation of Basic (5, 3) DWT Block in which ‘a’ and ‘b’ are
lifting coefficients (a = -1/2 and b = 1)

11. Simulation Results
DWT Block
Figure Simulation Result of DWT-1 Block with Both High and Low Pass

12. Figure Simulation Result of DWT-2 Block with Both High and
Low Pass Coefficients

13. Figure Simulation Result of DWT-3 Block with Both High and
Low Pass Coefficients

14. Applications of the project
• Medical application
• Signal de-noising
• Data compression
• Image processing

15. Conclusion
• Basically the medical images need more accuracy
without loss of information. The Discrete Wavelet
Transform (DWT) was based on time-scale
representation, which provides efficient multi-
resolution.
• It has been analyzed that the discrete wavelet
transform (DWT) operates at a maximum clock
frequency of 99.197 MHz respectively.

16. Future scope of the Work
As future work,
• This work can be extended in order to increase
the accuracy by increasing the level of
transformations.
• This can be used as a part of the block in the
full fledged application, i.e., by using these
DWT, the applications can be developed such
as compression, watermarking, etc.

17. THANK YOU