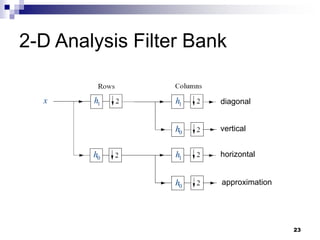
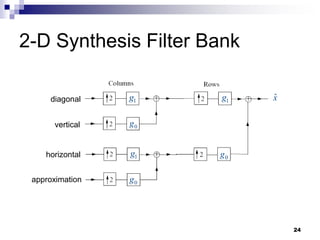
The document compares wavelet transforms and Fourier transforms. Wavelet transforms provide time-frequency localization while Fourier transforms only provide frequency localization. Wavelet transforms use small wave functions that are scaled and translated, allowing time-frequency localization. They also provide multiresolution analysis which is useful for applications like image processing. Wavelet transforms represent piecewise smooth signals like images and speech better than Fourier transforms as they require fewer coefficients around discontinuities. The document also discusses wavelet filter banks, discrete wavelet transforms, multiresolution analysis, and applications of wavelet transforms like image denoising.

1. Wavelet Transform
A very brief look

2. 2
Wavelets vs. Fourier Transform
 In Fourier transform (FT) we represent a
signal in terms of sinusoids
 FT provides a signal which is localized
only in the frequency domain
 It does not give any information of the
signal in the time domain

3. 3
Wavelets vs. Fourier Transform
 Basis functions of the wavelet transform
(WT) are small waves located in different
times
 They are obtained using scaling and
translation of a scaling function and
wavelet function
 Therefore, the WT is localized in both time
and frequency

4. 4
Wavelets vs. Fourier Transform
 In addition, the WT provides a
multiresolution system
 Multiresolution is useful in several
applications
 For instance, image communications and
image data base are such applications

5. 5
Wavelets vs. Fourier Transform
 If a signal has a discontinuity, FT produces
many coefficients with large magnitude
(significant coefficients)
 But WT generates a few significant
coefficients around the discontinuity
 Nonlinear approximation is a method to
benchmark the approximation power of a
transform

6. 6
Wavelets vs. Fourier Transform
 In nonlinear approximation we keep only a few
significant coefficients of a signal and set the
rest to zero
 Then we reconstruct the signal using the
significant coefficients
 WT produces a few significant coefficients for
the signals with discontinuities
 Thus, we obtain better results for WT nonlinear
approximation when compared with the FT

7. 7
Wavelets vs. Fourier Transform
 Most natural signals are smooth with a few
discontinuities (are piece-wise smooth)
 Speech and natural images are such signals
 Hence, WT has better capability for representing
these signal when compared with the FT
 Good nonlinear approximation results in
efficiency in several applications such as
compression and denoising

8. 8
Series Expansion of Discrete-Time Signals
 Suppose that is a square-summable sequence, that
is
 Orthonormal expansion of is of the form
 Where
is the transform of
 The basis functions satisfy the orthonormality
constraint
[ ]
x n
2
[ ] ( )
x n  Z
[ ]
x n
[ ] [ ], [ ] [ ] [ ] [ ]
k k k
k k
x n l x l n X k n
  
 
 
 
Z Z
*
[ ] [ ], [ ] [ ] [ ]
k k
l
X k l x l n x l
 
  
[ ]
x n
k

[ ], [ ] [ ]
k l
n n k l
  
 
2 2
x X


9. 9
 Haar expansion is a two-point avarage
and difference operation
 The basis functions are given as
 It follows that
Haar Basis
2
1 2 , 2 , 2 1
[ ]
0, otherwise
k
n k k
n

  
 

2 1
1 2 , 2
[ ] 1 2 , 2 1
0, otherwise
k
n k
n n k
 
 

   



2 0
[ ] [ 2 ],
k n n k
 
  2 1 1
[ ] [ 2 ]
k n n k
 
  

10. 10
 The transform is
 The reconstruction is obtained from
Haar Basis
 
2
1
[2 ] , [2 ] [2 1] ,
2
k
X k x x k x k

   
[ ] [ ] [ ]
k
k
x n X k n


 
Z
 
2 1
1
[2 1] , [2 ] [2 1]
2
k
X k x x k x k
 
    

11. 11
Two-Channel Filter Banks
 Filter bank is the building block of discrete-
time wavelet transform
 For 1-D signals, two-channel filter bank is
depicted below

12. 12
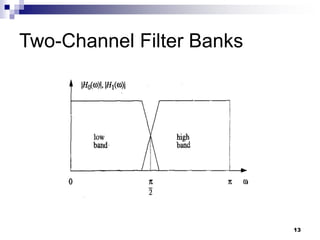
Two-Channel Filter Banks
 For perfect reconstruction filter banks we have
 In order to achieve perfect reconstruction the
filters should satisfy
 Thus if one filter is lowpass, the other one will be
highpass
x̂ x

0 0
1 1
[ ] [ ]
[ ] [ ]
g n h n
g n h n
  

  


13. 13
Two-Channel Filter Banks

14. 14
Two-Channel Filter Banks
 To have orthogonal wavelets, the filter bank
should be orthogonal
 The orthogonal condition for 1-D two-channel
filter banks is
 Given one of the filters of the orthogonal filter
bank, we can obtain the rest of the filters
1 0
[ ] ( 1) [ 1]
n
g n g n
   

15. 15
Haar Filter Bank
 The simplest orthogonal filter bank is Haar
 The lowpass filter is
 And the highpass filter
0
1
, 0, 1
[ ] 2
0, otherwise
n
h n

 

 


1
1
, 0
2
1
[ ] , 1
2
0, otherwise
n
h n n





   






16. 16
Haar Filter Bank
 The lowpass output is
 And the highpass output is
0 0 0
2
1 1
[ ] [ ]* [ ] [ ] [2 ] [2 ] [2 1]
2 2
n k
l
y k h n x n h l x k l x k x k


     

1 1 1
2
1 1
[ ] [ ]* [ ] [ ] [2 ] [2 ] [2 1]
2 2
n k
l
y k h n x n h l x k l x k x k


     


17. 17
Haar Filter Bank
 Since and , the filter
bank implements Haar expansion
 Note that the analysis filters are time-reversed
versions of the basis functions
since convolution is an inner product followed by
time-reversal
0[ ] [2 ]
y k X k
 1[ ] [2 1]
y k X k
 
0 0
[ ] [ ]
h n n

  1 1
[ ] [ ]
h n n

 

18. 18
Discrete Wavelet Transform
 We can construct discrete WT via iterated (octave-band) filter banks
 The analysis section is illustrated below
Level 1
Level 2
Level J

19. 19
Discrete Wavelet Transform
 And the synthesis section is illustrated here
 If is an orthogonal filter and , then we have an
orthogonal wavelet transform
0
V
1
V
2
V
J
V
1
W
2
W
J
W
[ ]
i
h n [ ] [ ]
i i
g n h n
 

20. 20
Multiresolution
 We say that is the space of all square-
summable sequences if
 Then a multiresolution analysis consists of
a sequence of embedded closed spaces
 It is obvious that
0
V
0 2( )
V 
2 1 0 2( )
J
V V V V
    
0 2
0
( )
J
j
j
V V

 

21. 21
Multiresolution
 The orthogonal component of in will
be denoted by :
 If we split and repeat on , , …., ,
we have
1
j
V 
1 1
j j j
V V W
 
 
j
V
1
j
W 
1 1
j j
V W
 

0
V 1
V 2
V 1
J
V 
0 1 1 J J
V W W W V
    

22. 22
2-D Separable WT
 For images we use separable WT
 First we apply a 1-D filter bank to the rows of the
image
 Then we apply same transform to the columns of
each channel of the result
 Therefore, we obtain 3 highpass channels
corresponding to vertical, horizontal, and
diagonal, and one approximation image
 We can iterate the above procedure on the
lowpass channel

23. 23
2-D Analysis Filter Bank
1
h
0
h
1
h
1
h
0
h
0
h
x diagonal
vertical
horizontal
approximation

24. 24
2-D Synthesis Filter Bank
x̂
diagonal
vertical
horizontal
approximation
1
g
1
g
1
g
0
g
0
g
0
g

25. 25
2-D WT Example
Boats image WT in 3 levels

26. 26
WT-Application in Denoising
Boats image Noisy image (additive Gaussian noise)

27. 27
WT-Application in Denoising
Boats image Denoised image using hard thresholding

28. 28
Reference
 Martin Vetterli and Jelena Kovacevic, Wavelets and
Subband Coding. Prentice Hall, 1995.