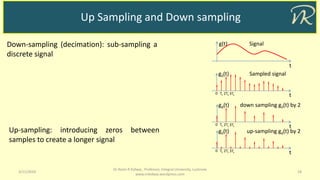
The document discusses various sampling methods for continuous signals, including ideal sampling, natural sampling, and flat top sampling, emphasizing the Nyquist criterion for accurate signal recovery. It explains the effects of aliasing in under-sampling and presents practical examples, such as the sampling process in audio CDs. Reconstruction techniques, such as zero order hold and the application of low pass filters, are also covered to illustrate how to recover the original signal from its samples.

1. Sampling
3/11/2019 1
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com
Sampling theorem, Ideal sampling, Flat top sampling, Natural sampling,
reconstruction of signals from samples, aliasing effect, up sampling and down
sampling, discrete time processing of continuous time signals

2. Sampling Theorem
3/11/2019 2
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com
A continuous time band limited signal can be represented by its samples, and can
be recovered from its samples,
provided that Sampling frequency s≥2m, (mmaximum frequency of signal)
The condition is referred as Nyquist criterion
Sampling
Continuous time
signal g(t)
Discrete time
signal g(t)
Sampling frequency S
t tTs0

3. Ideal Sampling
3/11/2019 3
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com
Let continuous time band limited signal be
0)(..)()(   m
GtsGtg 

Let periodic impulse train be
)(
1
)(or
])([*)(
2
1
)]([)(
)()()(signalSampledThen
2where;)()()(















n
s
s
n
ss
p
s
s
n
ss
k
sp
nG
T
G
nGtgFG
ttgtg
T
nTtt









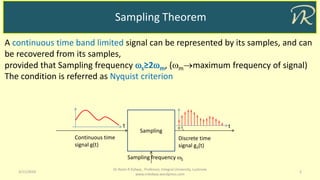
Discrete time signal g(t)
Ideal
SamplingContinuous time signal g(t)
Sampling
frequency S
t tTs0
p(t)
tTs0
1
Using linearity property of FT and convolution property of impulse




n
s
s
nG
T
tg )(
1
)(Thus 
Using multiplication property of FT

4. Ideal Sampling
3/11/2019 4
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com
g(t) Signal
t
g(t) Sampled signal
tTs 2Ts0 3Ts
p(t) Impulse train
tTs 2Ts0 3Ts
1
p()

s 2s0
s
-s-2s
G()
m-m
A



F[g(t)]
s 2s0
A/Ts
-s-2s
s> 2m
In Time domain:
Sampling results in conversion of
continuous time signal into discrete time
signal
In Frequency domain:
Sampling results in multiple translation of
signal spectrum (linear combination of
shifted signal spectrum at integer
multiples of sampling frequency.

5. Ideal Sampling: Reconstruction
3/11/2019 5
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com
Low Pass filter
Cut-off m




n
s
s
nG
T
tg )(
1
)(  )(
1
G
Ts
Amplifier
with gain Ts


 

otherwise
H m
L
0
1
)(


)(G
Reconstruction Filter
Sampled signal
tTs0
g(t)
g(t)
t
)(
1
tg
Ts

6. Sampling Example: Musical CD
3/11/2019 6
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com
Audio frequency range is 20Hz-20KHz.
Musical CD consists of two channels of music (for stereo sound) sampled at 44.1 KHz
(oversampling satisfying Nyquist criterion) and quantized to 16 bit. Compute the data size of CD
for 70 minutes music.
CD data= 2 x (44.1 x 103) x 16 x 60 x70 bits = 740.88 MB

7. Aliasing
3/11/2019 7
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com
g(t) Signal
t
g(t) Sampled signal
tTs 2Ts0 3Ts
G()
m-m
A


F[g(t)]
s 2s0
As
-s-2s
s> 2m
In case of under sampling (s<2m),
shifted versions of signal spectrum shall
overlap resulting in spectral distortions.
In such case, signal can not be recovered
from its samples. This effect is known as
ALIASING.
To avoid aliasing effect due to spurious
frequencies, a pre alias filter is applied
before sampling
F[g(t)]
s 2s0
As
-s-2s
s= 2m
s <2m
F[g(t)]
s 2s0
As
-s-2s
g(t) Sampled signal
tTs 2Ts0 3Ts
g(t) Sampled signal
tTs 2Ts0 3Ts


8. Flat Top Sampling
3/11/2019 8
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com
As ideal impulse can’t be generated, practical sampling pulse will exist for a duration.
In Flat top sampling, for each sample, the value is hold for a duration T.
Flat top sampling may be thought of as output of a system with impulse response h(t) shown
in figure to the input of ideal samples.
Ideal
SamplingContinuous time
signal g(t)
Sampling
frequency S
t
g(t)
tTs0
p(t)
tTs0
1
System with
impulse response
h(t)
tT
1
Ideal samples g(t) Flat top samples gF(t)
gF(t)
tTs0 T

9. Flat Top Sampling
3/11/2019 9
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com


























 

22
exp)(
0
22
12)(responseInput
T
Sa
Tj
TH
otherwise
T
t
T
T
Tt
rectth


)(
22
exp)(
)()()(

















n
s
s
F
F
nG
T
Sa
Tj
T
T
tG
tGHtG


 
 
  )(
22
exp2
1
)(Thus 
























 

n
s
ss
s
n
sF nG
T
Sa
Tj
T
T
T
Tnt
rectnTgtg 

FTofpropertyshifttimeand
2
pairFTUsing 










 T
SaT
T
t
rect


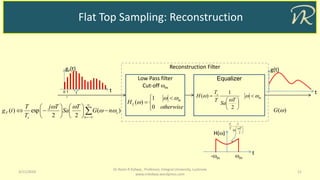
10. Flat Top Sampling
3/11/2019 10
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com
g(t) Signal
t
g(t) Sampled signal
tTs 2Ts0 3Ts
p(t) Impulse train
tTs 2Ts0 3Ts
1
p()

s 2s0
s
-s-2s
G()
m-m
A



F[g(t)]
s 2s0
As
-s-2s
s> 2m

F[gF(t)]
s 2s0
As
-s-2s
s> 2m
gF(t)
tTs0 T
Flat top sampling, introduces aperture effect as per sample function

11. Flat Top Sampling: Reconstruction
3/11/2019 11
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com
Low Pass filter
Cut-off m
Equalizer


 

otherwise
H m
L
0
1
)(


)(G
Reconstruction Filter g(t)
t
m
s
T
Sa
T
T
H 

 







2
1
)(
)(
22
exp)( 















n
s
s
F nG
T
Sa
Tj
T
T
tg 

gF(t)
tT
s
0 T
H()
t
-m m






2
1
T
Sa
T
Ts


12. Natural Sampling
3/11/2019 12
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com
In Natural sampling, each sample is pulse of duration T with amplitude varying in accordance
to signal value.
Natural sampling may be thought of multiplication of signal with pulse train.
Natural
SamplingContinuous time
signal g(t)
Sampling
frequency S
t
Natural samples gN(t)
gN(t)
tTs0 T
tTs0 T

13. Natural Sampling
3/11/2019 13
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com
 s
n
s
s
n
s
n
TjTn
SaT
T
TnTt
rect 

 



















 




 2
exp
2
2trainpulse
 
)(
22
exp)(
2
exp
2
*)(
2
1
)(
2)()(










































 

n
s
s
s
N
s
n
s
sN
n
s
N
nG
Tn
Sa
T
T
T
tG
n
TjTn
SaTGtG
T
TnTt
recttgtg






)(
22
exp)(Thus 















n
s
s
s
F nG
Tn
Sa
T
T
T
tg 


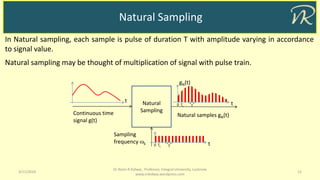
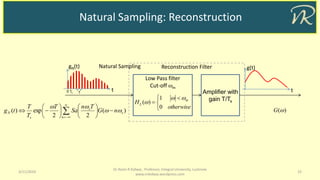
14. Natural Sampling
3/11/2019 14
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com
g(t) Signal
t

s 2s0
sT
-s-2s
G()
m-m
A



F[gN(t)]
s 2s0
As
-s-2s
s> 2m
tTs0 T
Pulse Train
Natural sampling, introduces amplitude scaling as per sample function at every shifted version
of G(), and not the aperture effect as in Flat top sampling.
gN(t) Natural Sampling
tTs0 T

15. Natural Sampling: Reconstruction
3/11/2019 15
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com
)(G
Low Pass filter
Cut-off m
Amplifier with
gain T/Ts


 

otherwise
H m
L
0
1
)(


Reconstruction Filter g(t)
t
)(
22
exp)( 















n
s
s
s
N nG
Tn
Sa
T
T
T
tg 

gN(t) Natural Sampling
tTs0 T

16. Zero Order Hold Reconstruction of Signals
3/11/2019 16
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com
g(t) Signal
tg(t) Sampled signal
tTs 2Ts0 3Ts
gZ(t) Zero order hold reconstruction
tTs 2Ts0 3Ts
Zero order hold reconstruction involve holding the
sampling value till next sample. It makes a staircase
approximation of the signal.
i.e. Zero order hold is special case of flat top sampling
with pulse width equal to sampling period gz(t)gF(t)TTs
 
)(
22
exp)(g
2
1
)()()(g






















n
s
ss
z
n s
s
sTTFz
nG
T
Sa
Tj
t
T
Tnt
rectnTgtgt
s


Exponential term in Spectrum of Zero order hold reflects delay by Ts/2, while sample
function term results in aperture effect causing distortion.

17. Zero Order Hold Reconstruction of Signals
3/11/2019 17
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com
Zero order hold can be achieved by simple holding circuit which holds sample value till next
sample
Low Pass filter
Cut-off m
Equalizer


 

otherwise
H m
L
0
1
)(


)(G
Reconstruction Filter g(t)
t
m
sT
Sa
H 

 







2
1
)(
H()
t
-m m






2
1
sT
Sa

gZ(t) Zero order hold
tTs 2Ts0 3Ts
)(
22
exp)(g 















n
s
ss
z nG
T
Sa
Tj
t 


18. Up Sampling and Down sampling
3/11/2019 18
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com
Up-sampling: introducing zeros between
samples to create a longer signal
Down-sampling (decimation): sub-sampling a
discrete signal
g(t) Signal
t
g(t) Sampled signal
tTs 2Ts0 3Ts
gd(t) down sampling g(t) by 2
tTs 2Ts0 3Ts
g(t) up-sampling gd(t) by 2
tTs 2Ts0 3Ts

19. Discrete Time Processing of Continuous time Signals
3/11/2019 19
Dr Naim R Kidwai, Professor, Integral University, Lucknow
www.nrkidwai.wordpress.com
Continuous time signals can be converted into discrete time using sampling and quantized to
make it digital. These discrete time signals can be processed using computer based discrete
time systems and output can be reconstructed as continuous time signal.
g(t) A/D converter
(Sampling/
Quantization)
Discrete time
system
D/A converter
(Reconstruction)
g(nTs)
=g[n]
y(nTs)
=y[n] y(t)