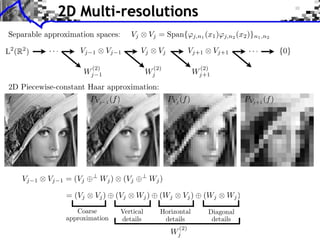
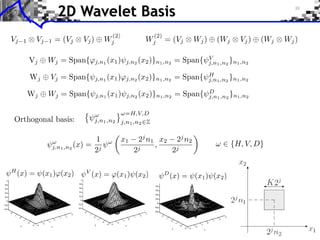
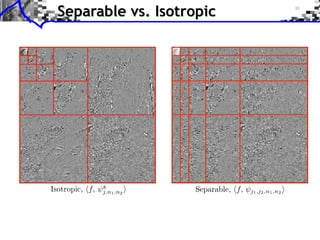
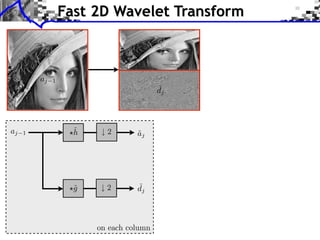
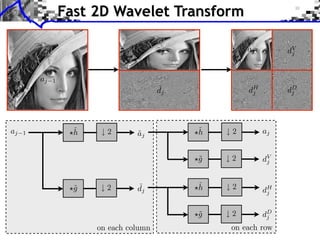
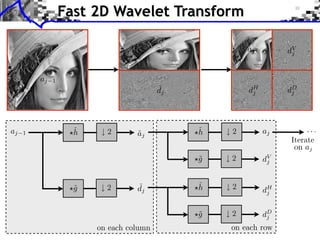
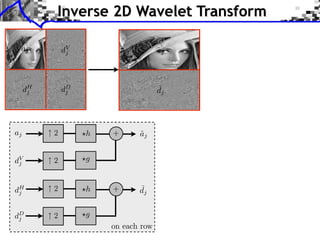
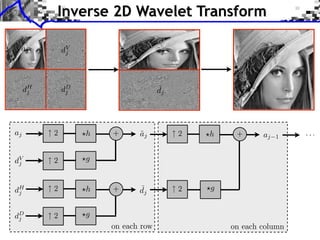
This document provides an overview of wavelet processing and wavelet transforms. It begins by reviewing Fourier transforms and introducing 1D multiresolutions and wavelet transforms. It describes the filter constraints for approximation and detail filters. It then discusses 2D multiresolutions and wavelet transforms, including anisotropic, separable, and isotropic transforms. It also covers fast wavelet transforms, discrete wavelet coefficients, and inverting the transform. The document concludes with examples of wavelet decompositions.


![The Four Settings
Note: for Fourier, bounded periodic.
Infinite continuous domains: f0 (t), t R ... ...
+⇥
ˆ
f0 ( ) = f0 (t)e i t
dt
⇥
Periodic continuous domains: f0 (t), t ⇥ [0, 1] R/Z
1
ˆ
f0 [m] = f0 (t)e 2i mt
dt
0
Infinite discrete domains: f [n], n Z ... ...
ˆ
f( ) = f [n]ei n
n Z
Periodic discrete domains: f [n], n ⇤ {0, . . . , N 1} ⇥ Z/N Z
N 1
ˆ
f [m] = f [n]e
2i
N mn
n=0](https://image.slidesharecdn.com/course-signal-wavelets-121213051330-phpapp02/85/Signal-Processing-Course-Wavelets-3-320.jpg)
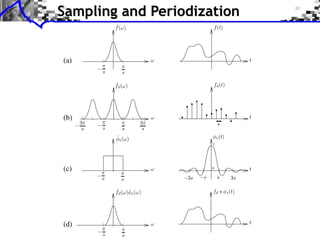
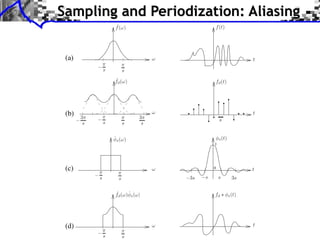
![Sampling and Periodization
f0 (t)
Sampling idealization:
(a)
f [n] = f0 (n/N )
(a)
f [n]
Poisson formula:
ˆ
f (⇥) = ˆ
f0 (N (⇥ + 2k ))
(b)
k
(b) ˆ
f0 ( )
Commutative diagram: (a) 1
1
sampling (a)
f0 (c) f 0
ˆ
f( )
cont. FT (c) discr. FT 0
periodization
ˆ
f0 ˆ
f (b)](https://image.slidesharecdn.com/course-signal-wavelets-121213051330-phpapp02/85/Signal-Processing-Course-Wavelets-4-320.jpg)


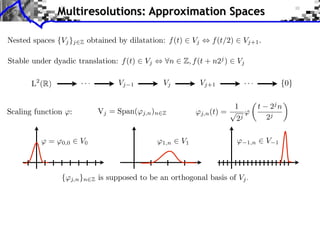
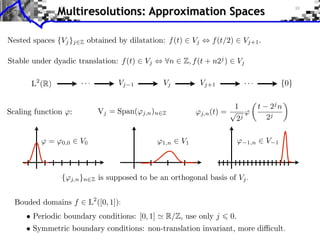
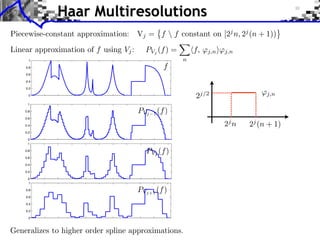
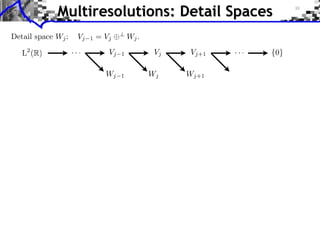




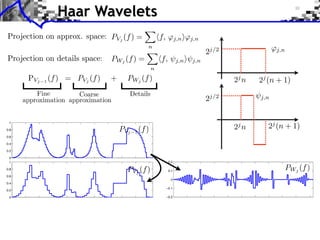
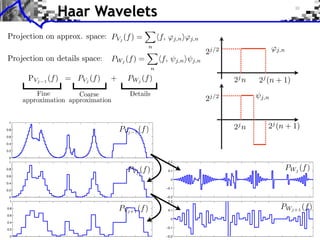




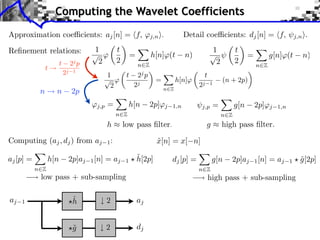
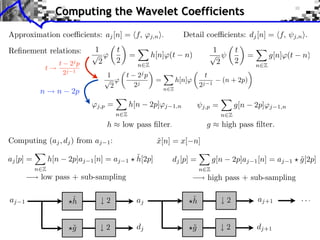
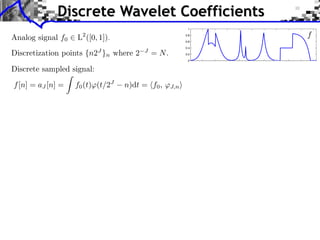
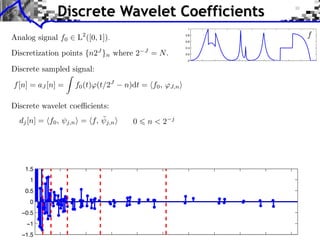
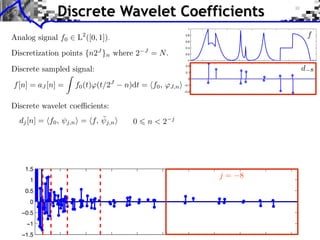
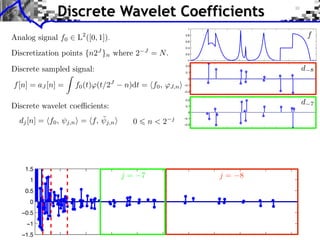
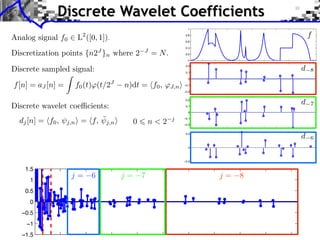
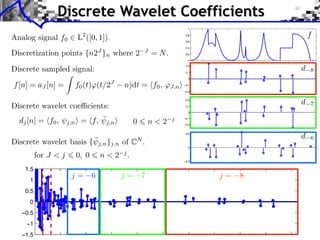
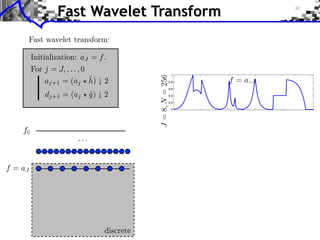
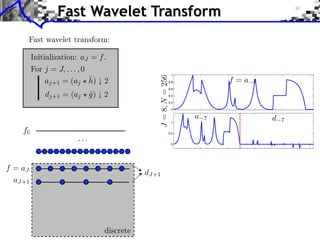
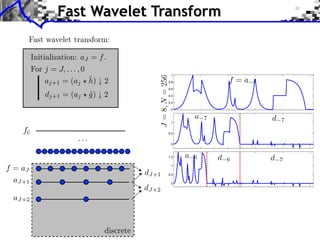
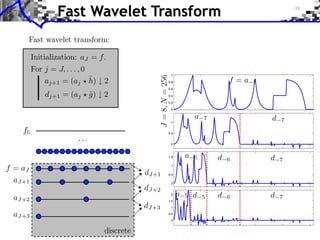
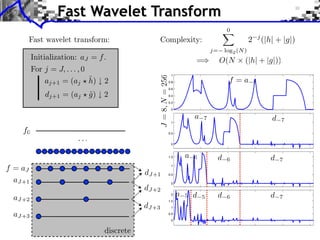
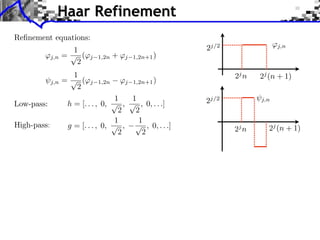
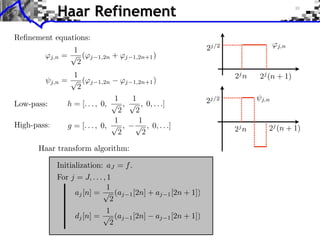
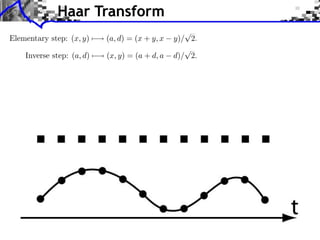
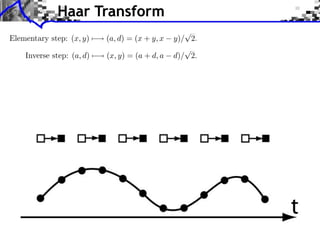
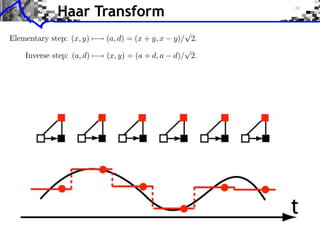
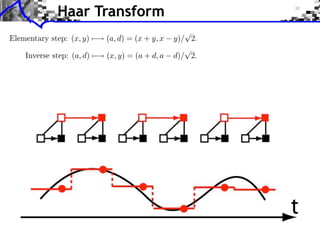
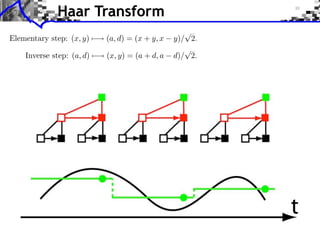

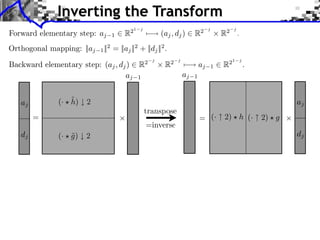
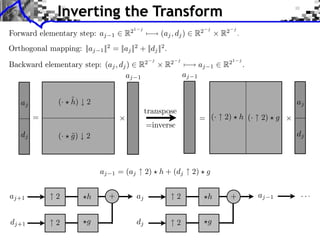



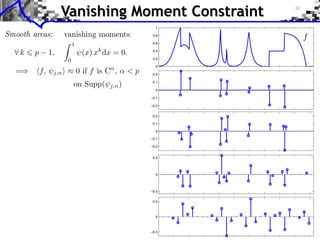
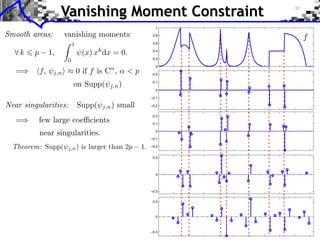
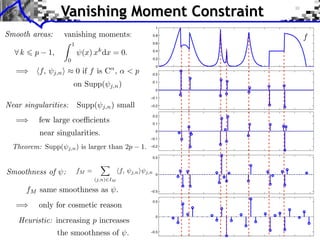
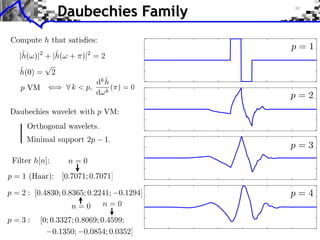
![Approximation Filter Constraints
{⌅(· n)}n orthogonal ⇥⇤ ⌅ n, ⌅ ⇧ ⌅(n) = [n] ⇥⇤
¯ |⌅(⇤ + 2k⇥)|2 = 1
ˆ
k](https://image.slidesharecdn.com/course-signal-wavelets-121213051330-phpapp02/85/Signal-Processing-Course-Wavelets-49-320.jpg)
![Approximation Filter Constraints
{⌅(· n)}n orthogonal ⇥⇤ ⌅ n, ⌅ ⇧ ⌅(n) = [n] ⇥⇤
¯ |⌅(⇤ + 2k⇥)|2 = 1
ˆ
k](https://image.slidesharecdn.com/course-signal-wavelets-121213051330-phpapp02/85/Signal-Processing-Course-Wavelets-50-320.jpg)
![Approximation Filter Constraints
{⌅(· n)}n orthogonal ⇥⇤ ⌅ n, ⌅ ⇧ ⌅(n) = [n] ⇥⇤
¯ |⌅(⇤ + 2k⇥)|2 = 1
ˆ
k](https://image.slidesharecdn.com/course-signal-wavelets-121213051330-phpapp02/85/Signal-Processing-Course-Wavelets-51-320.jpg)
![Approximation Filter Constraints
{⌅(· n)}n orthogonal ⇥⇤ ⌅ n, ⌅ ⇧ ⌅(n) = [n] ⇥⇤
¯ |⌅(⇤ + 2k⇥)|2 = 1
ˆ
k](https://image.slidesharecdn.com/course-signal-wavelets-121213051330-phpapp02/85/Signal-Processing-Course-Wavelets-52-320.jpg)
![Detail Filter Constraint
{ (· n)}n orthogonal n, ⇥ ⇤ ⇥(n) = [n] ⇥ ˆ
|⇥(⇤ + 2k )|2 = 1
k](https://image.slidesharecdn.com/course-signal-wavelets-121213051330-phpapp02/85/Signal-Processing-Course-Wavelets-53-320.jpg)
![Detail Filter Constraint
{ (· n)}n orthogonal n, ⇥ ⇤ ⇥(n) = [n] ⇥ ˆ
|⇥(⇤ + 2k )|2 = 1
k](https://image.slidesharecdn.com/course-signal-wavelets-121213051330-phpapp02/85/Signal-Processing-Course-Wavelets-54-320.jpg)
![Detail Filter Constraint
{ (· n)}n orthogonal n, ⇥ ⇤ ⇥(n) = [n] ⇥ ˆ
|⇥(⇤ + 2k )|2 = 1
k](https://image.slidesharecdn.com/course-signal-wavelets-121213051330-phpapp02/85/Signal-Processing-Course-Wavelets-55-320.jpg)
![Detail Filter Constraint
{ (· n)}n orthogonal n, ⇥ ⇤ ⇥(n) = [n] ⇥ ˆ
|⇥(⇤ + 2k )|2 = 1
k](https://image.slidesharecdn.com/course-signal-wavelets-121213051330-phpapp02/85/Signal-Processing-Course-Wavelets-56-320.jpg)
![Detail Filter Constraint
{ (· n)}n orthogonal n, ⇥ ⇤ ⇥(n) = [n] ⇥ ˆ
|⇥(⇤ + 2k )|2 = 1
k](https://image.slidesharecdn.com/course-signal-wavelets-121213051330-phpapp02/85/Signal-Processing-Course-Wavelets-57-320.jpg)