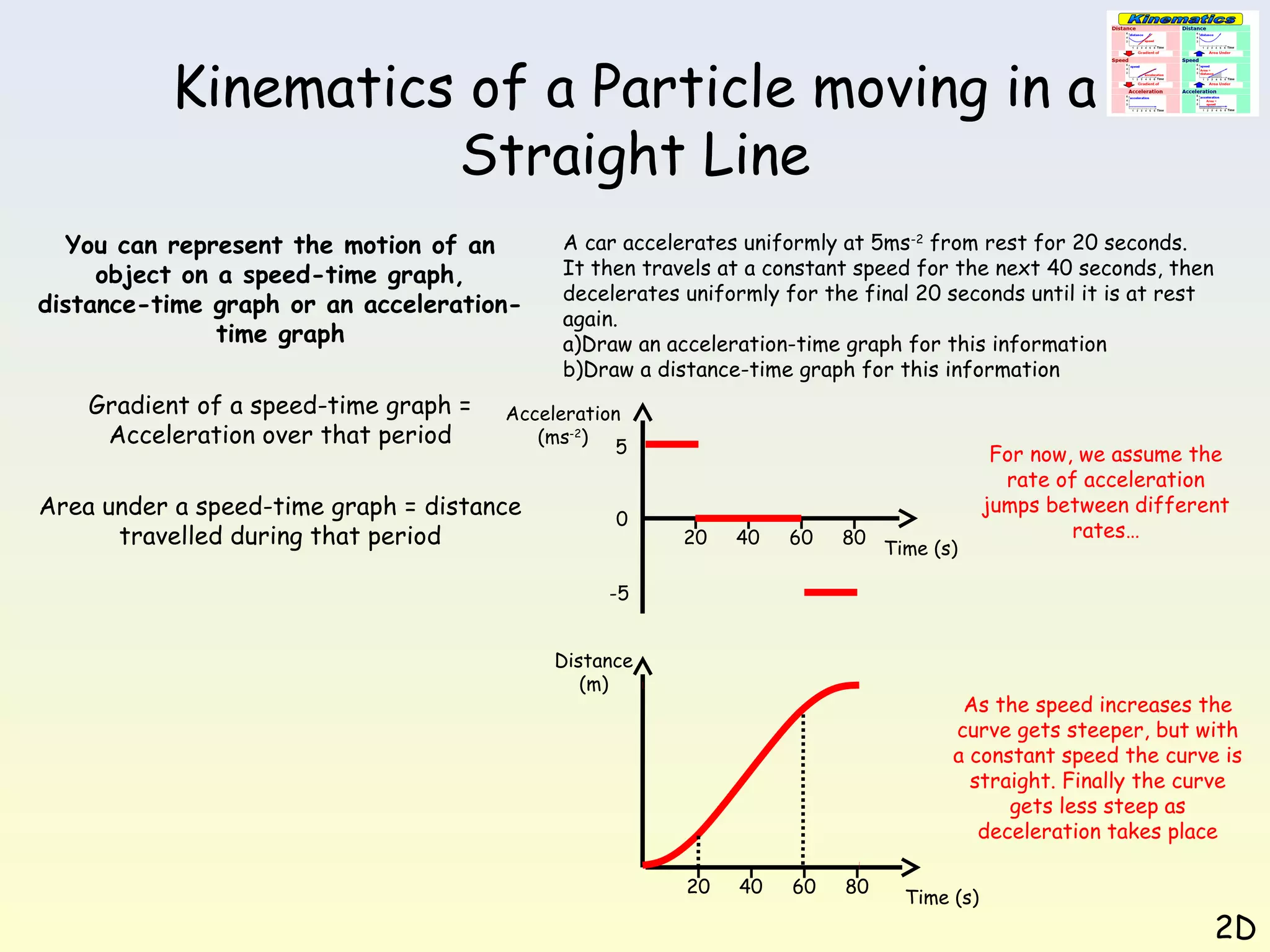
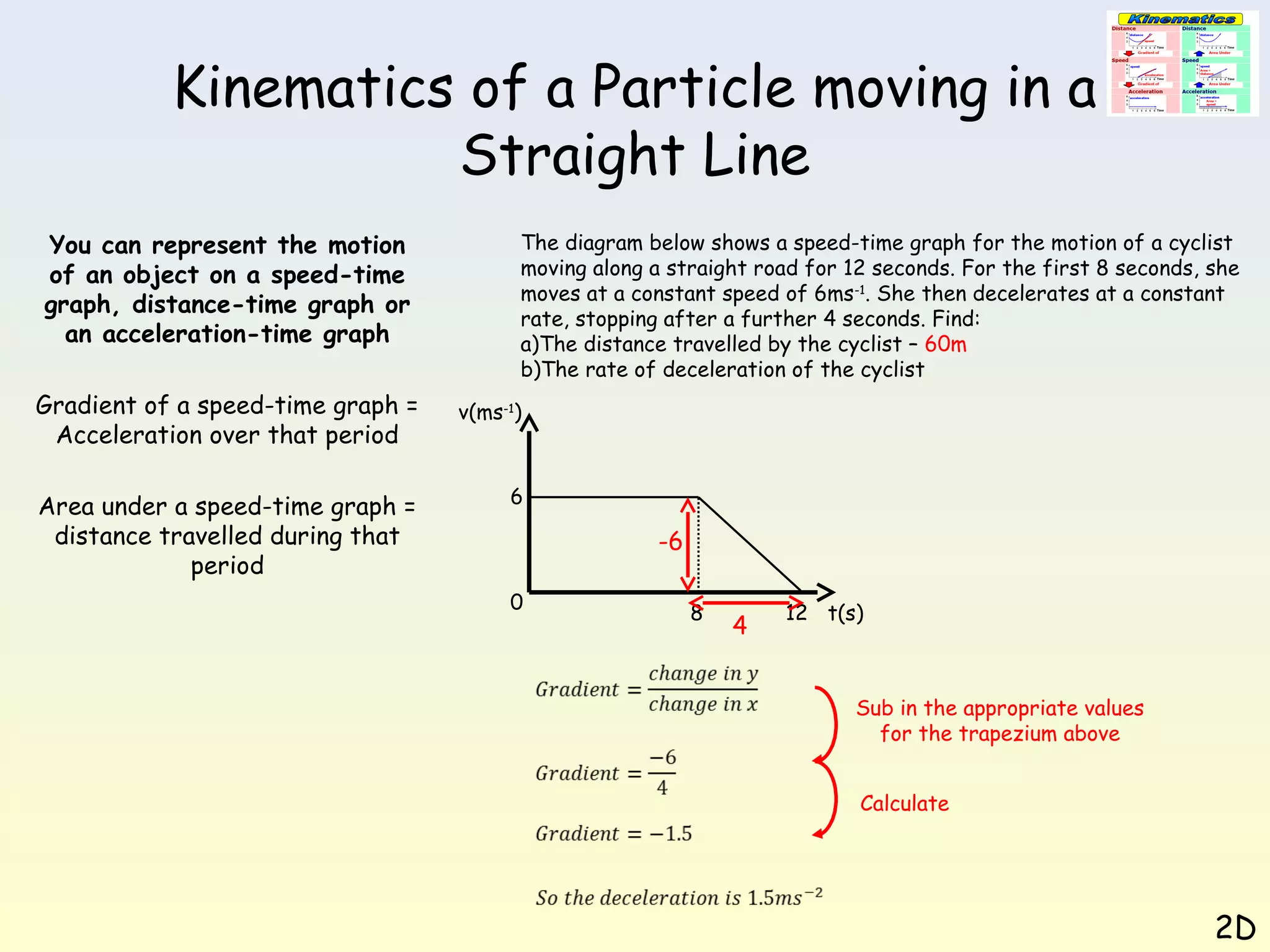
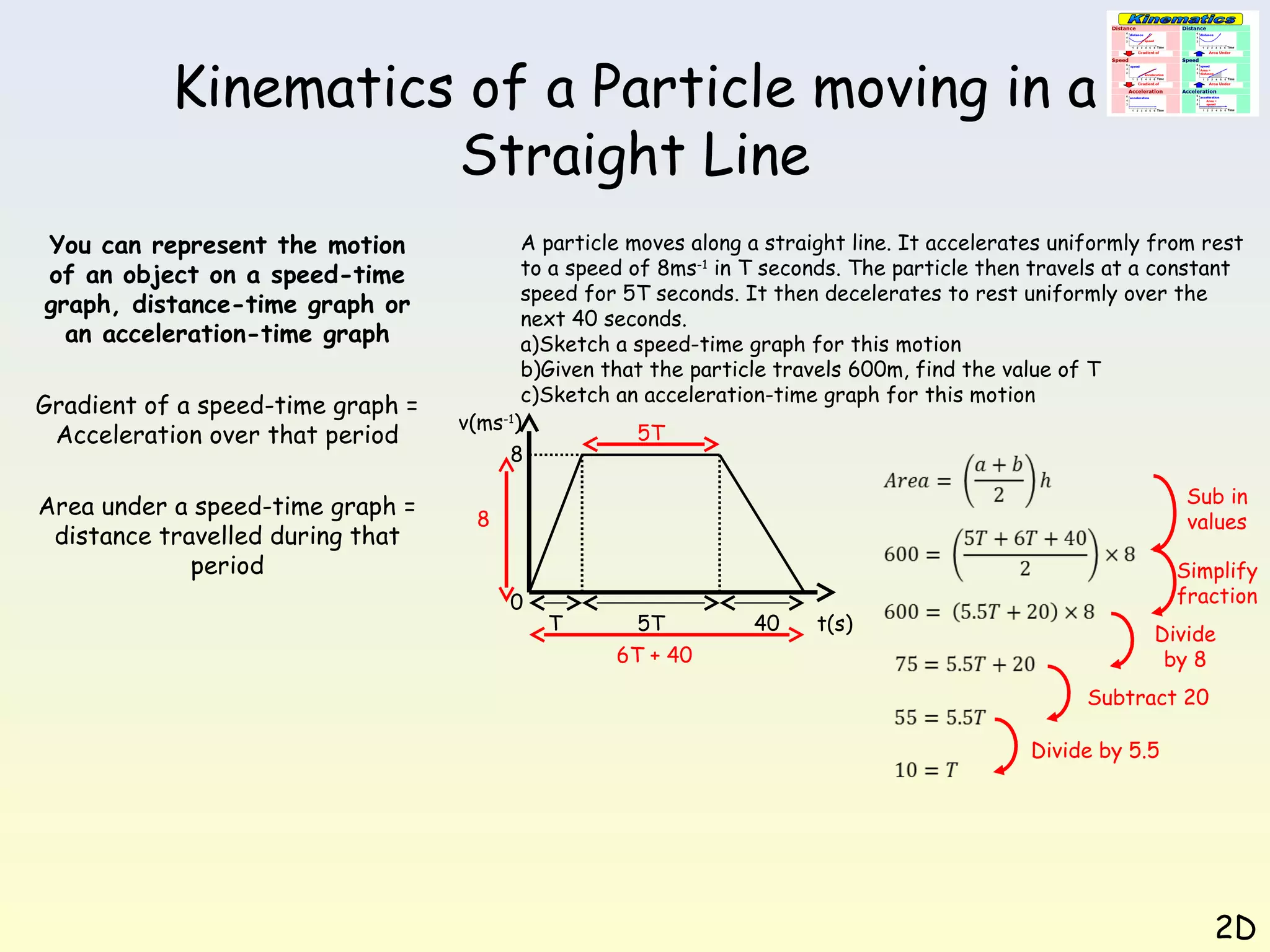
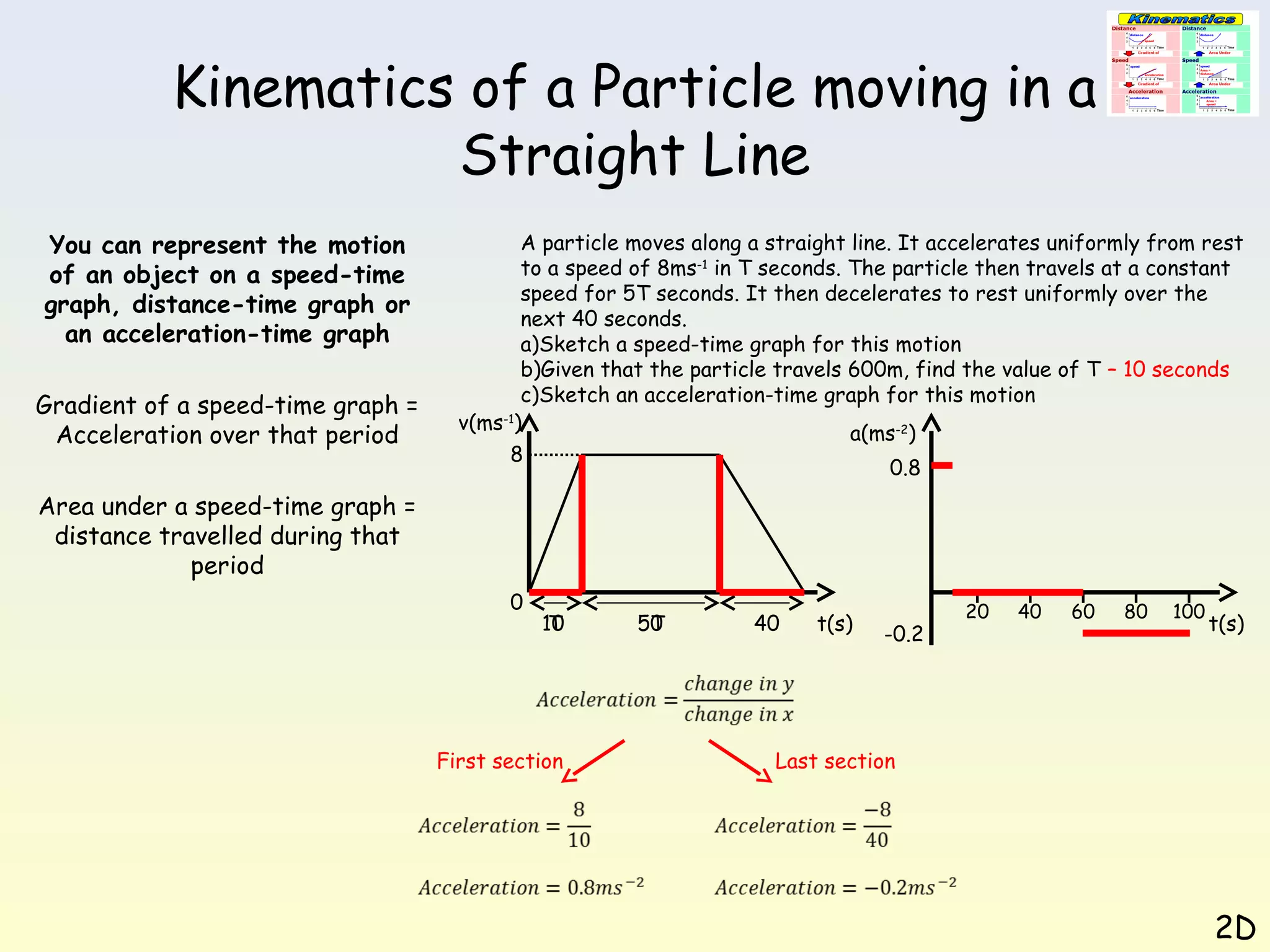
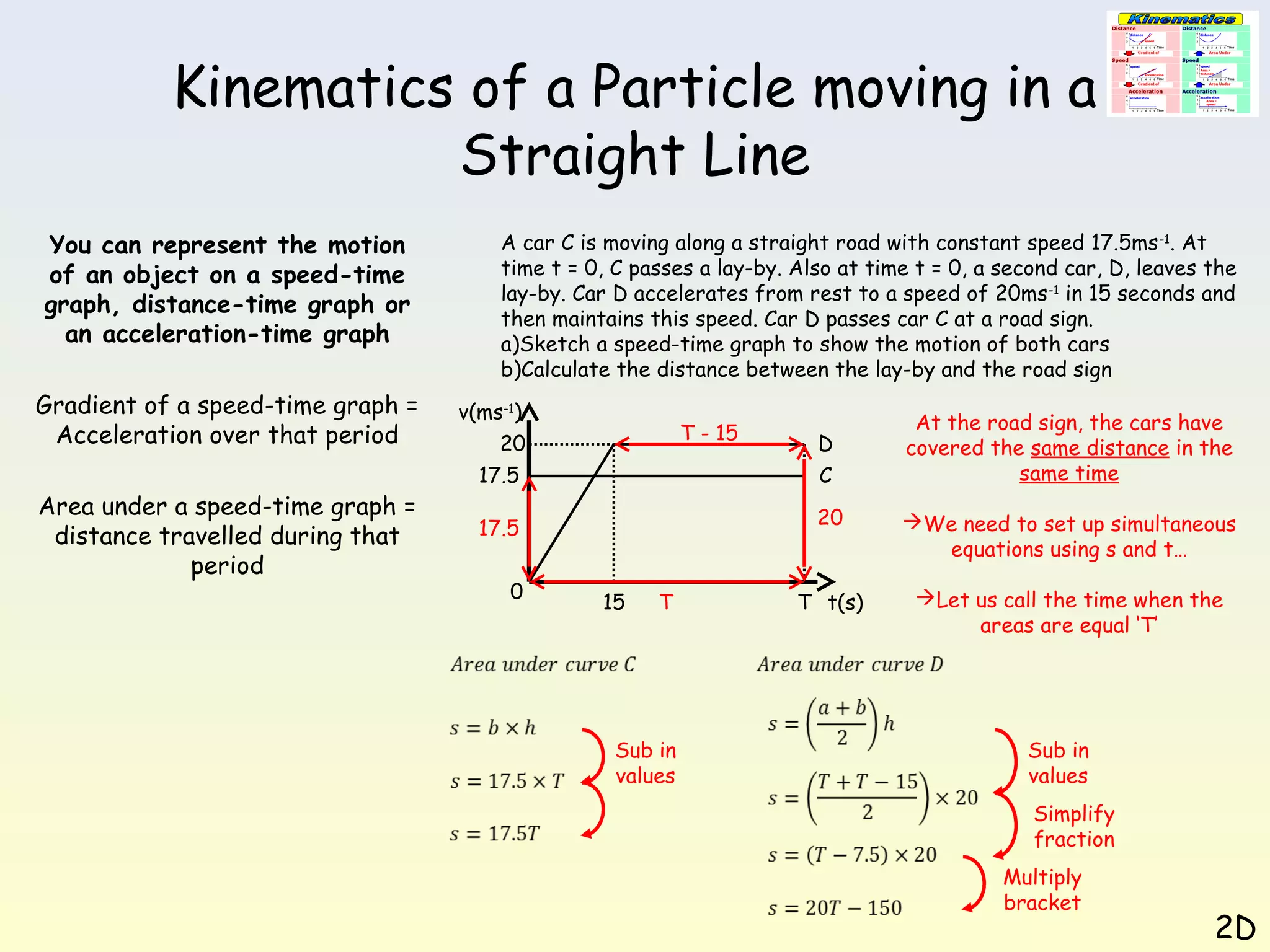
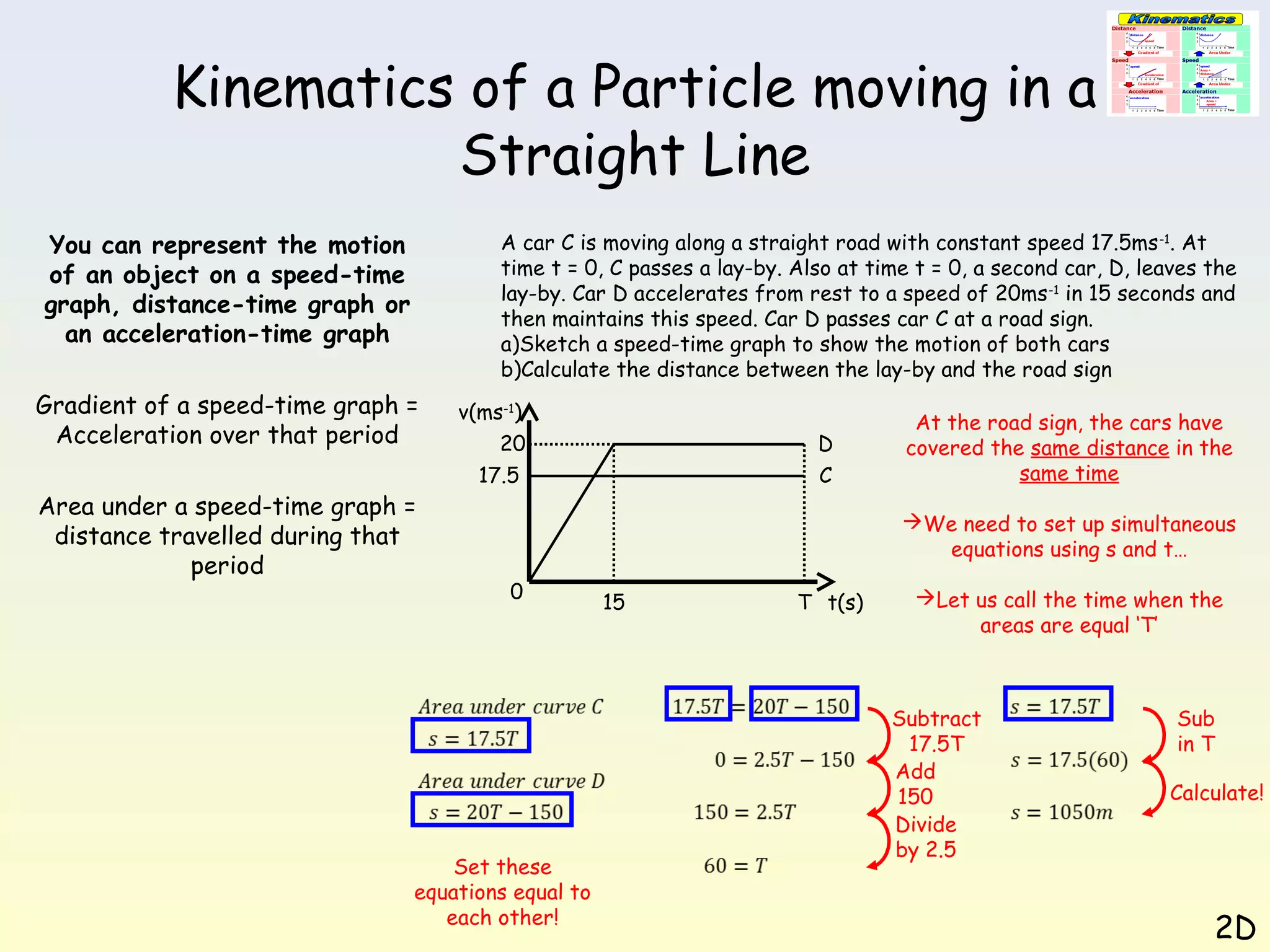
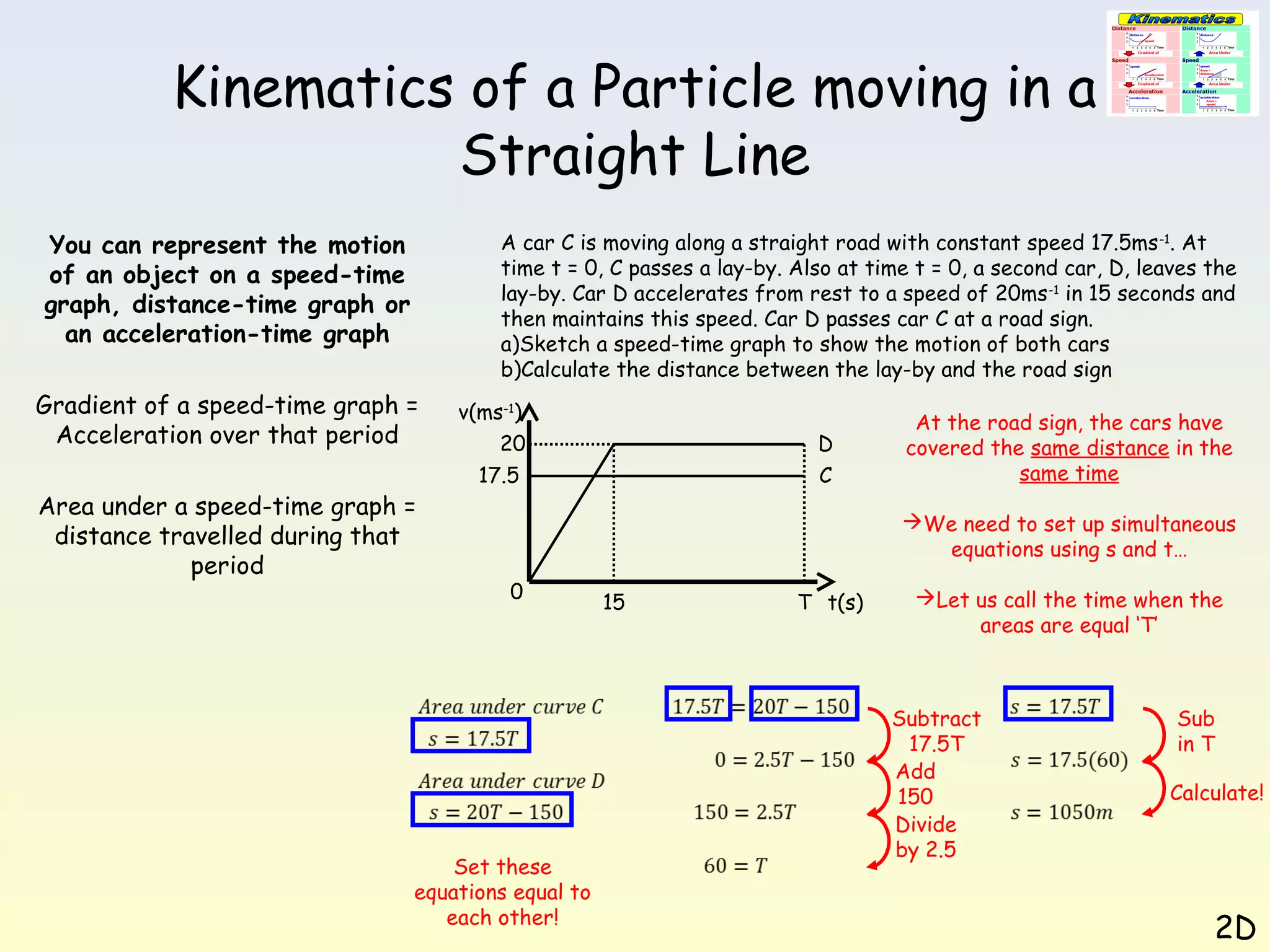
This document discusses kinematics of a particle moving in a straight line. It explains that motion can be represented using speed-time graphs, distance-time graphs, or acceleration-time graphs. The gradient of a speed-time graph represents acceleration, while the area under the graph represents distance traveled. Several examples are provided of constructing and interpreting these graphs to analyze different scenarios of linear motion.

2. Kinematics of a Particle moving in a
Straight Line
You can represent the motion of an
object on a speed-time graph,
distance-time graph or an accelerationtime graph
Final velocity v
v-u
u
Initial velocity
v
t
u
O
On a speed-time graph,
the gradient of a section
is its acceleration!
t
On a speed-time graph,
the Area beneath it is
the distance covered!
t
Time taken
2D

3. Kinematics of a Particle moving in a
Straight Line
You can represent the motion of an
object on a speed-time graph,
distance-time graph or an accelerationtime graph
Gradient of a speed-time graph =
Acceleration over that period
A car accelerates uniformly at 5ms-2 from rest for 20 seconds.
It then travels at a constant speed for the next 40 seconds, then
decelerates uniformly for the final 20 seconds until it is at rest
again.
a)Draw an acceleration-time graph for this information
b)Draw a distance-time graph for this information
Acceleration
(ms-2)
5
Area under a speed-time graph = distance
travelled during that period
0
20
40
60
80
Time (s)
For now, we assume the
rate of acceleration
jumps between different
rates…
-5
Distance
(m)
As the speed increases the
curve gets steeper, but with
a constant speed the curve is
straight. Finally the curve
gets less steep as
deceleration takes place
20
40
60
80
Time (s)
2D

4. Kinematics of a Particle moving in a
Straight Line
You can represent the motion
of an object on a speed-time
graph, distance-time graph or
an acceleration-time graph
The diagram below shows a speed-time graph for the motion of a cyclist
moving along a straight road for 12 seconds. For the first 8 seconds, she
moves at a constant speed of 6ms-1. She then decelerates at a constant
rate, stopping after a further 4 seconds. Find:
a)The distance travelled by the cyclist
b)The rate of deceleration of the cyclist
Gradient of a speed-time graph =
Acceleration over that period
v(ms-1)
Area under a speed-time graph =
distance travelled during that
period
6
8
6
0
12
8
12 t(s)
Sub in the appropriate values
for the trapezium above
Calculate
2D

5. Kinematics of a Particle moving in a
Straight Line
You can represent the motion
of an object on a speed-time
graph, distance-time graph or
an acceleration-time graph
The diagram below shows a speed-time graph for the motion of a cyclist
moving along a straight road for 12 seconds. For the first 8 seconds, she
moves at a constant speed of 6ms-1. She then decelerates at a constant
rate, stopping after a further 4 seconds. Find:
a)The distance travelled by the cyclist – 60m
b)The rate of deceleration of the cyclist
Gradient of a speed-time graph =
Acceleration over that period
v(ms-1)
Area under a speed-time graph =
distance travelled during that
period
6
-6
0
8
4
12 t(s)
Sub in the appropriate values
for the trapezium above
Calculate
2D

6. Kinematics of a Particle moving in a
Straight Line
You can represent the motion
of an object on a speed-time
graph, distance-time graph or
an acceleration-time graph
Gradient of a speed-time graph =
Acceleration over that period
Area under a speed-time graph =
distance travelled during that
period
A particle moves along a straight line. It accelerates uniformly from rest
to a speed of 8ms-1 in T seconds. The particle then travels at a constant
speed for 5T seconds. It then decelerates to rest uniformly over the
next 40 seconds.
a)Sketch a speed-time graph for this motion
b)Given that the particle travels 600m, find the value of T
c)Sketch an acceleration-time graph for this motion
v(ms-1)
5T
8
Sub in
values
8
0
T
5T
6T + 40
40
t(s)
Simplify
fraction
Divide
by 8
Subtract 20
Divide by 5.5
2D

7. Kinematics of a Particle moving in a
Straight Line
You can represent the motion
of an object on a speed-time
graph, distance-time graph or
an acceleration-time graph
Gradient of a speed-time graph =
Acceleration over that period
A particle moves along a straight line. It accelerates uniformly from rest
to a speed of 8ms-1 in T seconds. The particle then travels at a constant
speed for 5T seconds. It then decelerates to rest uniformly over the
next 40 seconds.
a)Sketch a speed-time graph for this motion
b)Given that the particle travels 600m, find the value of T – 10 seconds
c)Sketch an acceleration-time graph for this motion
v(ms-1)
a(ms-2)
8
0.8
Area under a speed-time graph =
distance travelled during that
period
0
10
T
First section
50
5T
40
t(s)
-0.2
20
40
60
80
100
t(s)
Last section
2D

8. Kinematics of a Particle moving in a
Straight Line
You can represent the motion
of an object on a speed-time
graph, distance-time graph or
an acceleration-time graph
Gradient of a speed-time graph =
Acceleration over that period
Area under a speed-time graph =
distance travelled during that
period
A car C is moving along a straight road with constant speed 17.5ms -1. At
time t = 0, C passes a lay-by. Also at time t = 0, a second car, D, leaves the
lay-by. Car D accelerates from rest to a speed of 20ms -1 in 15 seconds and
then maintains this speed. Car D passes car C at a road sign.
a)Sketch a speed-time graph to show the motion of both cars
b)Calculate the distance between the lay-by and the road sign
v(ms-1)
20
17.5
T - 15
At the road sign, the cars have
covered the same distance in the
same time
20
17.5
0
D
C
15
T
Sub in
values
We need to set up simultaneous
equations using s and t…
T t(s)
Let us call the time when the
areas are equal ‘T’
Sub in
values
Simplify
fraction
Multiply
bracket
2D

9. Kinematics of a Particle moving in a
Straight Line
You can represent the motion
of an object on a speed-time
graph, distance-time graph or
an acceleration-time graph
A car C is moving along a straight road with constant speed 17.5ms -1. At
time t = 0, C passes a lay-by. Also at time t = 0, a second car, D, leaves the
lay-by. Car D accelerates from rest to a speed of 20ms -1 in 15 seconds and
then maintains this speed. Car D passes car C at a road sign.
a)Sketch a speed-time graph to show the motion of both cars
b)Calculate the distance between the lay-by and the road sign
Gradient of a speed-time graph =
Acceleration over that period
Area under a speed-time graph =
distance travelled during that
period
v(ms-1)
20
17.5
D
C
At the road sign, the cars have
covered the same distance in the
same time
We need to set up simultaneous
equations using s and t…
0
Set these
equations equal to
each other!
15
T t(s)
Let us call the time when the
areas are equal ‘T’
Subtract
17.5T
Add
150
Divide
by 2.5
Sub
in T
Calculate!
2D

10. Kinematics of a Particle moving in a
Straight Line
You can represent the motion
of an object on a speed-time
graph, distance-time graph or
an acceleration-time graph
A car C is moving along a straight road with constant speed 17.5ms -1. At
time t = 0, C passes a lay-by. Also at time t = 0, a second car, D, leaves the
lay-by. Car D accelerates from rest to a speed of 20ms -1 in 15 seconds and
then maintains this speed. Car D passes car C at a road sign.
a)Sketch a speed-time graph to show the motion of both cars
b)Calculate the distance between the lay-by and the road sign
Gradient of a speed-time graph =
Acceleration over that period
Area under a speed-time graph =
distance travelled during that
period
v(ms-1)
20
17.5
D
C
At the road sign, the cars have
covered the same distance in the
same time
We need to set up simultaneous
equations using s and t…
0
Set these
equations equal to
each other!
15
T t(s)
Let us call the time when the
areas are equal ‘T’
Subtract
17.5T
Add
150
Divide
by 2.5
Sub
in T
Calculate!
2D