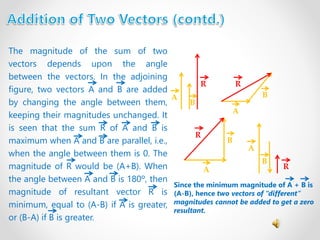
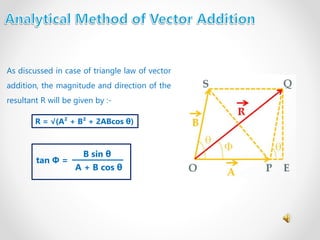
This document discusses scalar and vector quantities, defines vectors and their properties, and describes methods for vector addition and subtraction. It introduces concepts like the triangle law and parallelogram law of vector addition, multiplying vectors by scalars, position and displacement vectors, unit vectors, and resolving vectors into rectangular components. Key points covered include defining scalar/vector quantities, representing vectors with arrows, adding vectors using triangles/parallelograms, and properties like commutativity and associativity of vector addition.

2. • Scalar quantities :
Quantities which have only magnitude and no direction are called scalar
quantities, e.g. mass, distance, time, speed, volume, density, pressure,
work, energy, electric current, temperature, etc.
• Vector quantities :
Quantities which have magnitude as well as direction and obey the
triangle law of vector addition or equivalently the parallelogram law of
vector addition are called vector quantities, e.g. position, displacement,
velocity, force, acceleration, weight, momentum, impulse, electric field,
magnetic field, current density, etc.

3. A vector quantity can be represented by
an arrow. This arrow is called the ‘vector.’
The length of the arrow represents the
magnitude and the tip of the arrow
represents the direction. If a car A runs
with a velocity of 10 m/s towards east;
and another car B runs with a velocity of
20 m/s towards north-east. These
velocities can be represented by vectors
shown in the adjoining figure, taking
each unit of length on the arrow to
represent 5 m/s.
N
W E
S
Velocity of
car A
Velocity of
car B

4. Two or more vectors are said to be
equal if, and only if, they have the
same magnitude and same direction.
In the adjoining figure, A, B and C are
equal vectors.
If the direction of a vector is reversed,
the sign of the vector is reversed. This
new vector is called the “negative
vector” of the original vector. Here,
the vector D is the negative vector of
vectors A, B and C. Thus,
A = B = C = -D
A
B
C
D

5. Consider two vectors A and B.
1. First vector A is drawn.
2. Then starting from the arrow-head
of A, the vector B is drawn.
3. Now draw a vector R, starting from
the initial point of A and ending at
the arrow-head of B. Vector R would
be the sum of A and B.
R = A + B
The magnitude of A + B can be
determined by measuring the length of R
and the direction can be expressed by
measuring the angle between R and A
(or B).
A
B
R = A + B
We can start drawing from vector B also,
instead of vector A, as shown below:-
A
B
R’ = B + A

6. The vectors R and R’ obtained in the previous slide are
parallel to each other and their lengths and directions are
same. Hence,
R = R’
∴ A + B = B + A
Thus, addition of vectors is commutative.
This method of vector addition is called the method of
triangle of vectors.

7. There is another method of
adding two vectors, known as
the “method of parallelogram of
vectors.” According to this
method, sum of two vectors A
and B is a vector R represented
by the diagonal of a
parallelogram whose adjacent
sides are represented by vectors
A and B.
A
B

8. The magnitude of the sum of two
vectors depends upon the angle
between the vectors. In the adjoining
figure, two vectors A and B are added
by changing the angle between them,
keeping their magnitudes unchanged. It
is seen that the sum R of A and B is
maximum when A and B are parallel, i.e.,
when the angle between them is 0. The
magnitude of R would be (A+B). When
the angle between A and B is 180º, then
magnitude of resultant vector R is
minimum, equal to (A-B) if A is greater,
or (B-A) if B is greater.
A
R
B
A
B
R
A
B
R
A
B
R
Since the minimum magnitude of A + B is
(A-B), hence two vectors of “different”
magnitudes cannot be added to get a zero
resultant.

9. If more than two vectors are to be
added, then we first determine the sum
of any two vectors. The third vector is
then added to this sum and this method
is continued. Suppose we have to add
four vectors A, B, C and D as in the
adjoining figure. Then we proceed as
follows:-
R = (A + B) + C + D
R = (E + C) + D
R = F + D
C
A B
D
A
E C
B
F
D
R
The sum of vectors in each case is the
vector drawn to complete the polygon
formed by the given vectors. Hence this
method of addition of vectors is called
“polygon method.”

10. ** The vectors need not be added in the order seen in the last slide.
Vector C may be first added to vector A, then vector D and finally
vector B.
∴ R’ = A + C + D + B
But vector R and vector R’ are parallel, equal in length and are in
the same direction.
∴ R = R’
or, A + B + C + D = A + C + D + B
Hence vector addition is associative.
** If three or more vectors themselves complete a triangle or a
polygon, then their sum-vector or resultant vector cannot be
drawn. It means that the sum of these vectors is zero.

11. (i) Triangle Law of Vector Addition:-
This law states that if two vectors are represented in magnitude and direction
by the two sides of a triangle taken in the same order, then their resultant is
represented by the third side of the triangle taken in the opposite order.
Let two vectors A and B be represented,
both in magnitude and direction, by the
sides OP and PQ of a triangle OPQ taken
in the same order. Then the resultant R
will be represented by the closing side
OQ taken in the opposite order.
O P
Q
R
A
B
E
Φ θ

12. To find the magnitude of resultant R, a
perpendicular QE from Q on side OP produced
is drawn. Let ∠QPE = θ. Then, in right-angled
△OEQ, we have:-
OQ² = OE² + QE²
= (OP + PE)² + QE²
= OP² + PE² + 2.OP.PE + QE²
Now, PE² + QE² = PQ²
∴ OQ² = OP² + PQ² + 2.OP.PE
In right-angled △PEQ, we have cos θ =
∴ PE = PQ.cos θ
∴ OQ² = OP² + PQ² + 2.OP.PQ.cos θ
∴ R² = A² + B² + 2ABcos θ
PE
PQ
R = √(A² + B² + 2ABcos θ)

13. To find out the direction of the resultant,
suppose the resultant R makes an angle Φ with
the direction of vector A. Then,
QE
OE
tan Φ = =
Now OP = A and PE = Bcos θ. To find QE, we
consider △PEQ. We have:-
sin θ = , or, QE = PQ sin θ = B sin θ.
∴ tan Φ =
QE
OP + PE
QE
PQ
B sin θ
A + B cos θ

14. (ii) Parallelogram Law of Vector Addition:-
This law states that if two vectors are represented in magnitude and direction
by the two adjacent sides of a parallelogram drawn from a point, then their
resultant is represented in magnitude and direction by the diagonal of the
parallelogram drawn from the same point.
Let two vectors A and B inclined to each
other at an angle θ be represented in
magnitude and direction, by the sides OP
and OS of a parallelogram OPQS. Then,
according to parallelogram law, the resultant
of A and B is represented both in magnitude
and direction by the diagonal OQ of the
parallelogram.
B
S Q
Φ θ
A
R
θ
O P E

15. As discussed in case of triangle law of vector
addition, the magnitude and direction of the
resultant R will be given by :-
R = √(A² + B² + 2ABcos θ)
tan Φ =
B sin θ
A + B cos θ

16. (i) When two vectors are in the same direction : Then, θ = 0 so that
cos θ = cos 0º = 1 and sin θ = sin 0º = 0. Then we have :-
R = √(A² + B² + 2AB.cos 0º) = (A+B),
and tan Φ = = 0, i.e., Φ = 0.
B x 0
A + B
Thus, the resultant R has a magnitude equal to the sum of the magnitudes of the
vectors A and B and acts along the direction of A and B.
(ii) When two vectors are at right angle to each other : Then, θ = 90º so that
cos 90º = 0 and sin 90º = 1. Then,
R = √(A² + B² + 2AB.cos 90º) = √(A² + B²),
and tan Φ = =
B sin 90º
A + B cos 90º
B
A

17. (iii) When two vectors are in opposite directions : Then, θ = 180º, so that
cos 180º = -1 and sin 180º = 0.
∴ R = √(A² + B² + 2AB.cos 180º) = √(A-B)² = (A-B) or (B-A),
B sin 180º
and tan Φ = = 0, i.e., Φ = 0º or 180º.
A + B cos 180º
Thus, the magnitude of the resultant vector is equal to the difference of the
magnitudes of the two vectors and acts in the direction of the bigger vector.
Note:- The magnitude of the resultant of two vectors is maximum when they are in
the same direction, and minimum when they are in opposite directions.

18. Further in a parallelogram, if one diagonal is
the sum of two adjacent sides, then the other
diagonal is equal to its differences. In the
adjoining figure,
OQ = OP + PQ
PS = PQ + QS
But, QS = –OP
Thus, PS = PQ – OP

19. Suppose A and B are two vectors and the
vector B is to be subtracted from vector A. The
subtraction of B from A is same as addition of
–B to A, i.e., A – B = A + (–B).
Hence, to subtract vector B from A, first we
reverse B to get –B. Then the vector –B is
added to vector A. For this, we first draw
vector A and then starting from the arrow-head
of A, we draw the vector –B, and finally
we draw a vector R from the initial point of A
to the arrow-head of –B. Thus, vector R is the
sum of A and –B, i.e., the difference A – B :-
R = A + (–B) = A – B.
A
B
A
-B
A
-B
R = A – B

20. On multiplying a vector A by a scalar or a number k, a vector R (say) is
obtained :-
R = k A
The magnitude of R is k times the magnitude of A and the direction of R is
same as that of A. If k is a pure number having no unit, then the unit of R
will be same as that of A. If a vector A is 5 cm long and directed towards east,
then vector 2 A would be 10 cm long and directed towards east; and the
vector -2 A would be 10 cm long but directed towards west.

21. If k is a physical quantity having a unit, then the unit of R will be obtained by
multiplying the units of k and A. In this case, the vector R will represent a new
physical quantity. For example, if we multiply a vector v (velocity) by a scalar
m (mass) then their multiplication p (say) will represent a new vector quantity
called momentum :-
p = m v
The unit of mass m is kg and the unit of velocity v is m/s. Hence, the unit of p
will be kg.m/s. The direction of p will be same as that of v.

22. To describe the motion of an object in a plane, we use the concept of
position and displacement vectors. For this, we select a point in the plane as
origin and describe the position of the object with respect to that origin.
Y
P
Q
r1
r2
O X
Suppose, at an instant of time t1, the object is at a point P in
the X-Y plane of a cartesian coordinate system. Then a
vector OP drawn from origin O to the point P is called the
position vector of the object at time t1. It may be written as
r1, where r1 is the distance of the point P from the origin O.
If the object moves to a point Q at time t2, then OQ or r2 is
the position vector of the object at time t2, where r2 is the
distance of the point Q from the origin O.

23. Y
P
Q
r1
r2
O X
The vector PQ drawn from the point P to the point Q is the
displacement vector of the object during the interval t2 – t1.
The vector PQ is the vector difference OQ – OP (since
OP + PQ = OQ by triangle law of vector addition), i.e.,
PQ = r2 – r1
Thus, the displacement vector is the difference between the
final and the initial position vectors.

24. If two vectors A and B are equal, then their difference A – B is defined as zero vector
or null vector and is denoted as 0.
A – B = 0, if A = B.
Thus, zero vector is a vector of zero magnitude having no specific direction. Its initial
and terminal points are coincident.
Properties:-
• A + 0 = A
• n 0 = 0
• 0 A = 0

25. Though a zero vector does not quite fit in our description of a vector as it
has no specific direction, in this way it is considered as one of the non-proper
vectors. Still it is needed in vector algebra due to the following
reasons :-
• What is A – B when A = B?
• What is A + B + C if these vectors form a closed figure?
• We know that with respect to origin in cartesian coordinate system, position
vector of a point P is OP, then what’s the position vector of origin itself?
• What is the displacement vector of a stationary object?
• What is the acceleration vector of an object moving with a constant velocity?
Answer to all these questions is a zero vector.

26. A vector whose magnitude is unity is called a “unit vector”.
If A is a vector whose magnitude A ≠ 0, then A / A is a unit vector whose direction is
the direction of A. The unit vector in the direction of A is written as A. Thus,
^ A
^
A = or, A = A A
^
A
Thus, any vector in the direction of unit vector may be written as the product of the
unit vector and the scalar magnitude of that vector.
Orthogonal Unit Vectors:- The unit vectors
along the X-axis, Y-axis and Z-axis of the right-handed
cartesian coordinate system are written
^ ^ ^
as i, j, and k respectively. These are called
orthogonal unit vectors.
Y
^
O X
Z
^
j
i
^k

27. The resolution of a vector is opposite to vector addition. If a vector is resolved into
two vectors whose combined effect is the same as that of the given vector, then the
resolved vectors are called the “components” of the given vector. If a vector is
resolved into two vectors which are mutually perpendicular, then these vectors are
called the “rectangular components” of the given vector.
Let us suppose that a given vector A is to be
resolved into two rectangular components. For this,
taking the initial point of A as origin O, rectangular
axes OX and OY are drawn. Then perpendiculars are
dropped on OX and OY from the arrow-head of A.
These perpendiculars intersect OX and OY at P and
Q respectively. Then the vectors Ax and Ay drawn
from O to P and Q are the rectangular components
of vector A. From rectangle OQRP, it is clear that the
vector A is the sum of vectors Ax and Ay :-
A = Ax + Ay.
By measuring OP and OQ, the magnitudes of Ax
and Ay can be determined.
X
Y
Q R
O
P
A
θ
Ax
Ay

28. ^ ^
Now let i and j be unit vectors along X and Y axes
respectively, and Ax and Ay the scalar magnitudes of
Ax and Ay respectively. Then, we may write :-
^ ^
Ax = Ax i and Ay = Ay j
Thus, we have :-
^ ^
A = Ax i + Ay j
This is the equation for vector A in terms of its
rectangular components in a plane. If the vector A
makes an angle θ with the X-axis, then we have :-
Ax = A cos θ and Ay = A sin θ
From these equations, we have :-
A = √(Ax² + Ay²)
θ = tan -1(Ay / Ax)
Thus, if we know the magnitudes Ax and Ay of the
rectangular components of A, then from above two
equations, we can determine respectively the
magnitude and direction of vector A.

29. The multiplication of two vector quantities cannot be done by simple
algebraic method. The product of two vectors may be a scalar as well as a
vector. For example, both ‘force’ and ‘displacement’ are vector quantities.
Their product may be ‘work’ as well as ‘moment of force’. Work is a scalar
but moment of force is a vector quantity.
Vector quantities are represented by vectors. If the product of two vectors is
a scalar quantity, then it is called ‘scalar product’; if the product is a vector
quantity then it is called ‘vector product.’ If A and B are two vectors, then
their scalar product is written as A ∙ B (read A dot B), and the vector product
is written as A x B (read A cross B). Hence, the scalar product is also called
‘dot product’ and the vector product is also called ‘cross product.’

30. The scalar product of two vectors is defined as a
scalar quantity equal to the product of their
magnitudes and the cosine of the angle between
them. Thus, if θ is the angle between A and B, then,
A ∙ B = A B cos θ,
where A and B are the magnitudes of A and B. The
quantity AB cos θ is a scalar quantity.
θ
A
B
Now, B cos θ is the component of vector B in the direction of A. Hence, the
scalar product of two vectors is equal to the product of the magnitude
of one vector and the component of the second vector in the direction
of the first vector.

31. (i) Power P is the rate of doing work. We know that :-
Work W = Force F ∙ Displacement S
W
t t
∴ = F ∙
Hence, Power P = F ∙ v
Thus, power is the scalar product of force and velocity.
(ii) The magnetic flux (Φ) linked with a plane is defined as scalar product of
uniform magnetic field B and vector area A of that plane :-
Φ = B ∙ A
S

32. (i) The scalar product is commutative.
A ∙ B = B ∙ A
(ii) The scalar product is distributive.
A ∙ (B + C) = A ∙ B + A ∙ C
(iii) The scalar product of two mutually perpendicular vectors is zero.
(iv) The scalar product of two parallel vectors is equal to the product of their
magnitudes.
(v) The scalar product of a vector with itself is equal to the square of the
magnitude of the vector.
^ ^ ^
(vi) The scalar product of unit orthogonal vectors i, j, k have the following
relations :-
^ ^ ^ ^ ^ ^
^ ^ ^ ^ ^ ^
i ∙ j = j ∙ k = k ∙ i = 0
i ∙ i = j ∙ j = k ∙ k = 1
(vii) The scalar product of two vectors is equal to the sum of the products of their
corresponding x-, y-, z- components. A ∙ B = AxBx + AyBy + AzBz

33. The vector product of two vectors is defined as a vector having a
magnitude equal to the product of the magnitudes of the two vectors and
the sine of the angle between them, and having the direction perpendicular
to the plane containing the two vectors. Thus, if A and B be two vectors, then
their vector product, written as A x B, is a vector C defined by :-
^
C = A x B = AB sin (A, B) n,
where A and B are the magnitudes of A and B; (A, B) is the angle between them
^
and n is a unit vector perpendicular to the plane of A and B.
^
The direction of C (or n) is perpendicular to the plane containing A and B and
its sense is decided by right-hand screw rule.

34. (i) Suppose there is a particle P of mass m whose
position vector is r w.r.t the origin O of an inertial
reference frame. Let p (= m v) be the linear momentum
of the particle. Then, the angular momentum J of the
particle about the origin O is defined as the vector
product of r and p, i.e.,
J = r x p
Its scalar magnitude is J = r p sin θ,
where θ is the angle between r and p.
(ii) The instantaneous linear velocity v of a particle is
equal to the vector product of its angular velocity ω
and its position vector r with reference to some origin,
i.e., v = ω x r
Z
Y
X
O
θ
J
r p
P

35. (i) The vector product is “not” commutative, i.e.,
A x B ≠ B x A
(ii) The vector product is distributive, i.e.,
A x (B + C) = A x B + A x C
(iii) The magnitude of the vector product of two vectors mutually at right angles is equal to the
product of the magnitudes of the vectors.
(iv) The vector product of two parallel vectors is a null vector (or zero).
(v) The vector product of a vector by itself is a null vector (zero), i.e.,
A x A = 0
^ ^ ^
^ ^
^ ^
(vi) The vector product of unit orthogonal vectors i, j, k have the following relations :-
^ ^
^
(a) i x j = –j x i = k
^
^
^
j x k = –k x j = i
^ ^ ^
^ ^
k x i = –i x k = j
^ ^ ^ ^ ^ ^
(b) i x i = j x j = k x k = 0
(vii) The vector product of two vectors in terms of their x-, y- and z- components can be
expressed as a determinant.

36. Name:- Pankaj Bhootra
Class:- 11 C
Physics Project