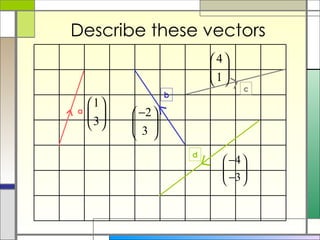
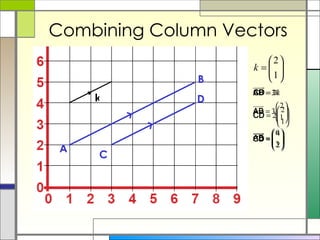
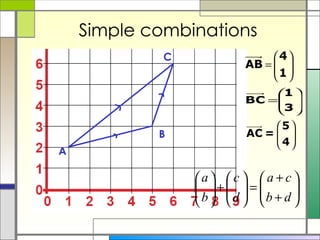
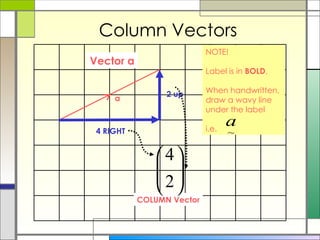
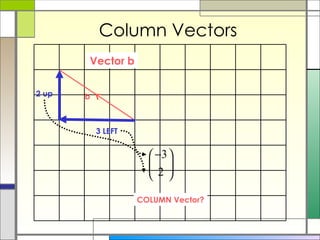
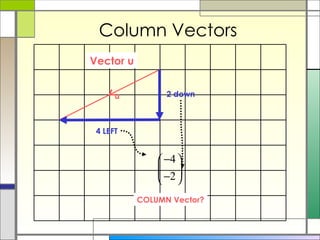
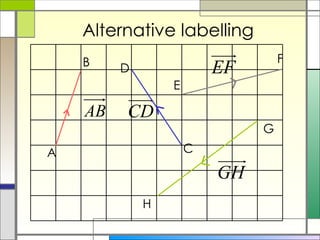
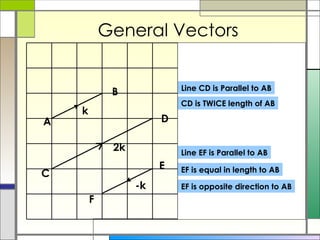
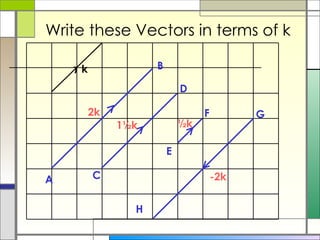
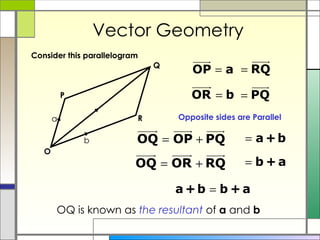
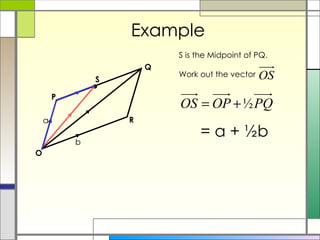
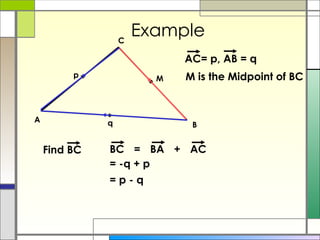
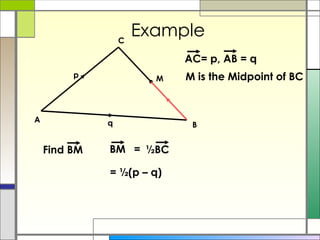
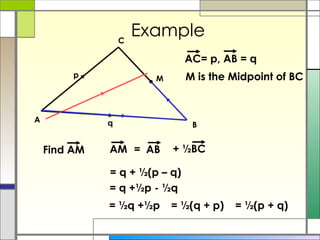
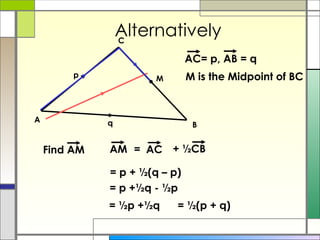
1) A vector describes both the direction and magnitude of motion of an object. Vectors can be represented as column vectors or general vectors. 2) Column vectors are labeled with bold letters and a wavy line underneath. They represent vertical and horizontal components. General vectors can be positioned anywhere and represent motion using a single length and direction. 3) The resultant of two vectors is the same no matter the route taken to get there. It can be used to find unknown vectors in geometric figures.

1. Vectors By Aruna

2. A VECTOR? Describes the motion of an object A Vector comprises Direction Magnitude We will consider Column Vectors General Vectors Vector Geometry Size

3. Column Vectors Vector a COLUMN Vector 4 RIGHT 2 up a NOTE! Label is in BOLD . When handwritten, draw a wavy line under the label i.e.

4. Column Vectors Vector b COLUMN Vector? 3 LEFT 2 up b

5. Column Vectors Vector u COLUMN Vector? 4 LEFT 2 down n

6. Describe these vectors b a c d

7. Alternative labelling A B C D F E G H

8. General Vectors A Vector has BOTH a Length & a Direction k can be in any position All 4 Vectors here are EQUAL in Length and Travel in SAME Direction. All called k k k k k

9. General Vectors A B C D -k 2k F E Line CD is Parallel to AB CD is TWICE length of AB Line EF is Parallel to AB EF is equal in length to AB EF is opposite direction to AB k

10. Write these Vectors in terms of k A B C D E F G H 2k 1½k ½k -2k k

11. Combining Column Vectors k A B C D

12. Simple combinations A B C

13. Vector Geometry Consider this parallelogram Opposite sides are Parallel OQ is known as the resultant of a and b Q O P R a b

14. Resultant of Two Vectors Is the same, no matter which route is followed Use this to find vectors in geometrical figures

15. Example = a + ½b Q O P R a b . S S is the Midpoint of PQ. Work out the vector

16. Alternatively = a + ½b = b + a - ½b = ½b + a Q O P R a b . S S is the Midpoint of PQ. Work out the vector

17. Example M is the Midpoint of BC = -q + p = p - q A B C p q M Find BC AC= p, AB = q BC BA AC = +

18. Example M is the Midpoint of BC = ½(p – q) A B C p q M Find BM AC= p, AB = q BM ½BC =

19. Example M is the Midpoint of BC = q + ½(p – q) = q +½p - ½q = ½q +½p = ½(q + p) = ½(p + q) A B C p q M Find AM AC= p, AB = q AM + ½BC = AB

20. Alternatively M is the Midpoint of BC = p + ½(q – p) = p +½q - ½p = ½p +½q = ½(p + q) A B C p q M Find AM AC= p, AB = q AM + ½CB = AC