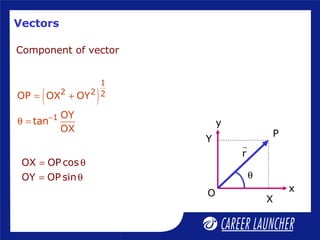
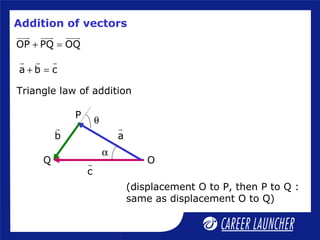
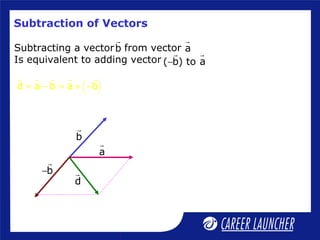
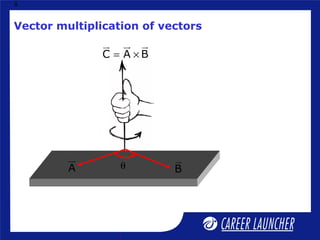
This document provides an overview of physics concepts related to kinematics and vectors, including: 1. It defines scalars and vectors, and gives examples such as displacement being a vector quantity. 2. It covers vector concepts such as position vectors, unit vectors, and vector components. 3. It discusses vector addition and subtraction using the triangle law and parallelogram law. 4. It introduces scalar and vector multiplication, including the dot product and cross product of vectors. 5. It includes several examples and class exercises to demonstrate applying concepts like finding vector components, adding vectors, and determining the angle between two vectors.

1. Physics

2. Session
Kinematics - 1

3. Session Opener
You fly from Delhi to Mumbai
New Delhi
Mumbai
Hyderabad
•
•
•
Then you fly from Mumbai to Hyderabad
Does it mean that you have flown
from Delhi to Hyderabad ?

4. Session Objectives
1. Scalars and vectors
2. Definitions
3. Vector addition and vector subtraction
4. Components of vectors
5. Multiplication of vectors

5. Scalars And Vectors
Scalars : physical quantities that can
be completely specified by
just numbers.
Vectors : physical quantities that cannot be
completely specified by their magnitude
alone. They also need a ‘direction’
specification.
For instance, displacement is a vector quantity.

6. Vectors
OP : Position vector
uuur
Length OP meter
Directed from O to P.
Both r and θ are needed to specify P
Vectors also obey the law a b b a+ = +
r r r r
O x
y
P
θ
r
r

7. Vectors
Component of vector
( )
1
2 2 2
1
OP OX OY
OY
tan
OX
−
= +
θ =
OX OP cos
OY OP sin
= θ
= θ
O x
y
P
θ
r
r
X
Y

8. Unit Vectors
O x
y
P
θ
r
r
X
Y
Unit vector : vector with magnitude
of unity
= =
= θ + θ
r
r
r
r
ˆ ˆr , r one unit
r
ˆ ˆr i r cos j r sin
O
x
y
θ
ˆrˆj
ˆi

9. Class Exercise

10. Class Exercise - 6
∧ ∧ ∧ ∧
= + = +
ur ur
A 3 i 4 j ; B 7 i 24 j .
Find such that C = B and is in
the direction of .
ur
C
ur
Cur
A
The unit vector in the direction of ,
where 5 is the magnitude of . Magnitude of
the vector = 25 units. Hence the value of
∧ ∧
+
=
ur 3 i 4 j
A
5ur
Aur
B
∧ ∧
∧ ∧
 
+ 
= = + 
  
ur 3 i 4 j
C 25 15 i 20 j
5
Solution :

11. Vector Definitions
Null vector : vector with zero
magnitude
Equal Vectors : ˆˆa b aa bb= ⇒ =
r r
If a = b
Direction of both are the same ˆˆa b=

12. Addition of vectors
OP PQ OQ+ =
uuur uuur uuur
(displacement O to P, then P to Q :
same as displacement O to Q)
Triangle law of addition
a b c+ =
r r r
O
P
Q
b
r
a
r
c
r
α
θ

13. Addition of vectors
Parallelogram law
From geometry : ( )
1/2
2 2
c a b 2abcos= + + θ
bsin
tan
a bcos
θ
α =
+ θ
a b c+ =
r r r
b
r
a
r
c
r
αθ
a
b
θ
bsinθ
bcosθ

14. Subtraction of Vectors
Subtracting a vector from vector
Is equivalent to adding vector
b
r
a
r
( b) to a−
r r
( )d a b a b= − = + −
r r r r r
b
r
a
r
b−
r
d
r

15. Class Exercise

16. Class Exercise - 1
The maximum resultant of 2 vectors
is 18 units. The resultant magnitude
is 12. If the resultant is
perpendicular to the smaller vector ,
find the magnitude of the two
vectors.
R
A
B
A + B = 18 [The maximum amplitude of
the resultant is when they are collinear.]
Also 122
+ A2
= (18 – A)2
.
Solving, we get
A = 5 and B = 13
Solution :

17. Class Exercise - 2
+ =
ur ur ur
A B R , + =
ur ur ur
A 2B P ,
ur
P
is perpendicular to . Then
ur
A
(a) A = B (b) A + B = R
(c) A = R (d) B = R
Since the given triangle is a
right-angled triangle B = R,
where point O is the mid point of
the hypotenuse.
P
A
B
B
R
o
Solution :

18. Class Exercise - 3
The components along the X and Y-axis of
are 3 m and 4 m respectively. The
components along X and Y-axis of the
vectors is 2 m and 6 m respectively.
Find the components of along X and Y-
axis?
ur
A
+
ur ur
A B ur
B
∧ ∧ ∧ ∧ ∧ ∧
= + + + + = +
ur
Let B x i y j .Then (3 x) i (4 y) j 2 i 6 j
So x = –1 and y = 2.
∧ ∧
= +
ur
Hence B – i 2 j
Solution :

19. Class Exercise - 4
A man swims across a river that flows
at 3 m/s. The man moves in a
direction directly perpendicular to the
flow of the river at 4 m/s. If the width
of the river is 100 m, then find the
time taken by the man to reach the
opposite bank.

20. Solution - 4
r
R
m
m r R . m, r , R
→ → → → → →
+ = denote
the components of velocities of man,
river and resultant during the motion.
The resultant direction in which the
man moves is not along the shortest
line joining the two banks. But
nevertheless the component of the
velocities in the Y direction is 4 m/s.
Hence the man takes , i.e 25 s to
cross over to the opposite bank.
100
4

21. Multiplication of vector by a real
number
a multiplied by λ
r
b a a a= λ ⇒ λ = λ
r r r r
If is negativeλ
c a= −λ
r r
Direction : opposite a
r

22. Scalar multiplication of vectors
Scalar product (dot product)
x x y yc a.b abcos a b a b= = θ = +
r r
a.b is scalar.
a.b b.a=
r r
r r r r
b
r
a
r
bcosθ
θ

23. Class Exercise

24. Class Exercise - 8
∧ ∧ ∧ ∧ ∧ ∧
= + = +
ur ur
A 5 i 7 j– 3k;B 2 i 2 j– ck .
If the two vectors are perpendicular
to each other, then find c.
If the vectors A and B are perpendicular
to each other, then × =
ur ur
A B 0
× = + + = =−
ur ur
Therefore A B 10 14 3c 0. So,c 8
Solution :

25. Class Exercise - 9
What is the angle between the two
vectors
∧ ∧ ∧ ∧ ∧ ∧
= + + = +
ur ur
A –2 i 3 j k ; B i 2 j– 4k ?
A·B = AB cosθ = –2 + 6 – 4 = 0. Hence the
two vectors are perpendicular to each
other.
Solution :

26. Class Exercise - 10
Find the component of the vector
in the direction of
the vector .
∧ ∧ ∧
= + +
ur
A 3 i 4 j 5k ∧ ∧
= +
ur
B 3 i 4 j
A·B = AB cosθ. This also means that A.B is the
product of the magnitude of B and the magnitude
of the component of A in the direction of B.
Magnitude of B = 5 units.
A·B = 25. Hence the magnitude of the component of
A in the direction of B is 5, which can happen only if
the component vector is .
∧ ∧
+3 i 4 j
Alternately, if we compare the components of the two
vectors along the X, Y directions, we find that they are
the same. Hence the component of A in the direction of
B must be same as the vector B.
Solution :

27. Vector multiplication of vectors
Vector product (cross product)
ˆc a b is vector absin c= × = θ
r r r
( )x y y x
ˆc k a b a b= −
r
a b b a× = − ×
r r r r b
r
a
r
θ

28. Vector multiplication of vectors
Vector product has an
orientation given by the
right-hand thumb rule.
Curl palm of your right hand from
the first vector to the second vector
keeping the thumb upright. The
direction of the thumb gives the
direction of resultant.

29. Vector multiplication of vectors
A
ur
θA
ur
B
ur
C A B= ×
ur ur ur

30. Product of two vectors
ˆˆ ˆi j k
ˆˆ ˆj k i
ˆ ˆ ˆk i j
× =
× =
× =
Some special cases
(ii) For unit vectors
ˆ ˆˆ ˆ ˆ ˆi i 0 j j k k× = = × = × = = =ˆ ˆˆ ˆ ˆ ˆi . i j. j k. k 1
=
=
=
ˆ ˆi. j 0
ˆˆj.k 0
ˆ ˆk . i 0
× = θ =
ur ur
A B AB sin 0(i) (for parallel vectors)
= θ =
ur ur
A.B AB cos 0 (for perpendicular vectors)

31. Class Exercise

32. Class Exercise - 7
What is the torque of a force
acting
at the point
and about the origin?
∧ ∧ ∧ 
= + ÷ ÷
 
r
F 2 i – 3 j 4k N
∧ ∧ ∧
= + +
r
r 3 i 2 j 3k
 τ = × 
r r r
Note r F
Solution :
∧ ∧ ∧ ∧ ∧ ∧
= + + = +
r r
r 3 i 2 j 3k,F 2 i – 3 j 4k
∧ ∧ ∧ ∧ ∧ ∧ ∧
= × = + + + =
r
F r f –9k– 12 j – 4k 8 i 6 j 9 i 17 i
Hence the moment of the force

33. Class Exercise - 5
The angle between two forces of
equal magnitude acting at a point,
such that the resultant force also has
the same magnitude is___.
Solution :
F
F
R=F
θ
120∴ θ = o
2 2 2
2 2
R F F 2F.F cos (but R F given)
F 2F (1 cos )
= + + θ =
= + θ
1
1 cos
2
1
cos
2
⇒ = + θ
⇒ θ = −

34. Thank you