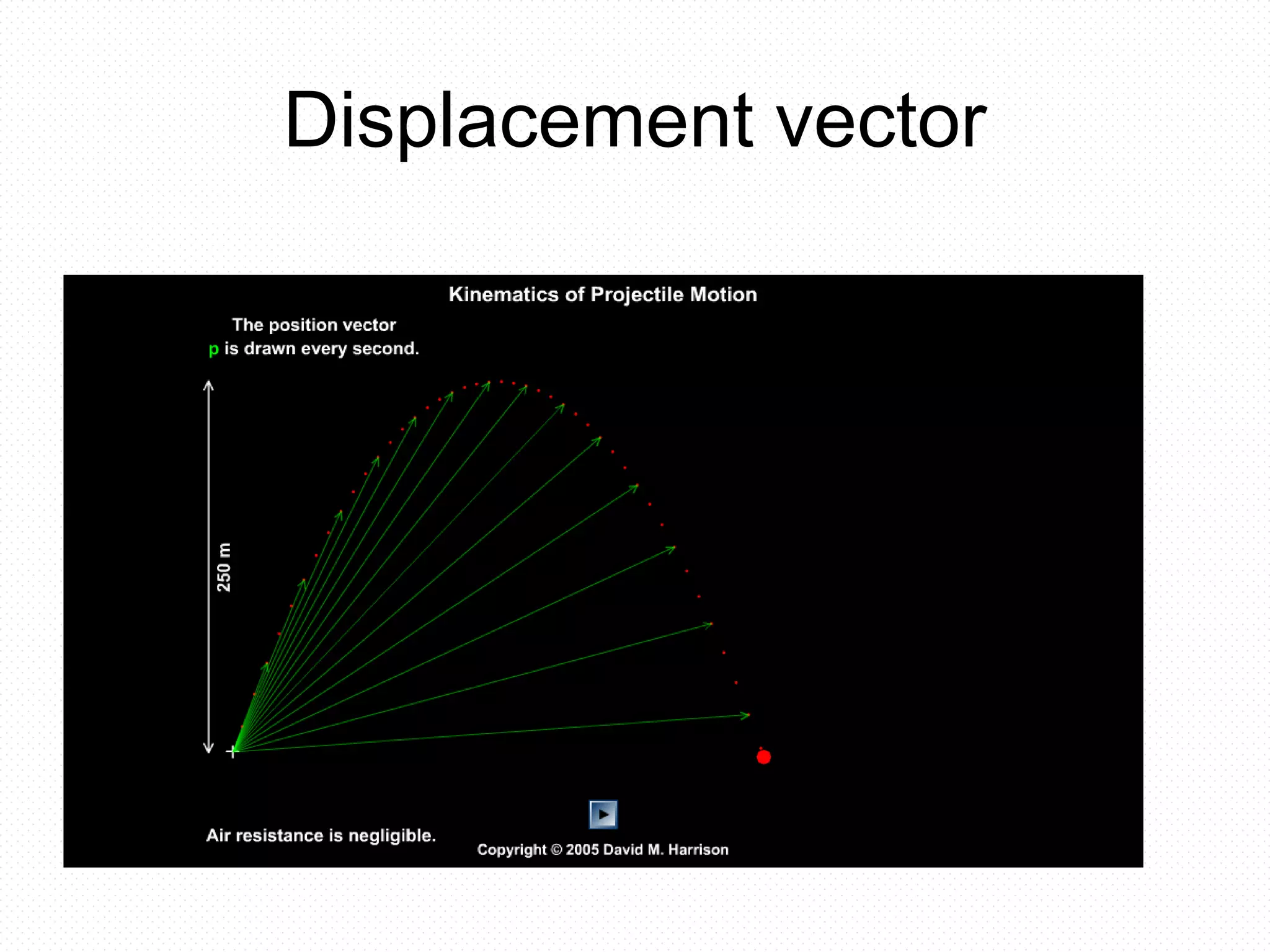
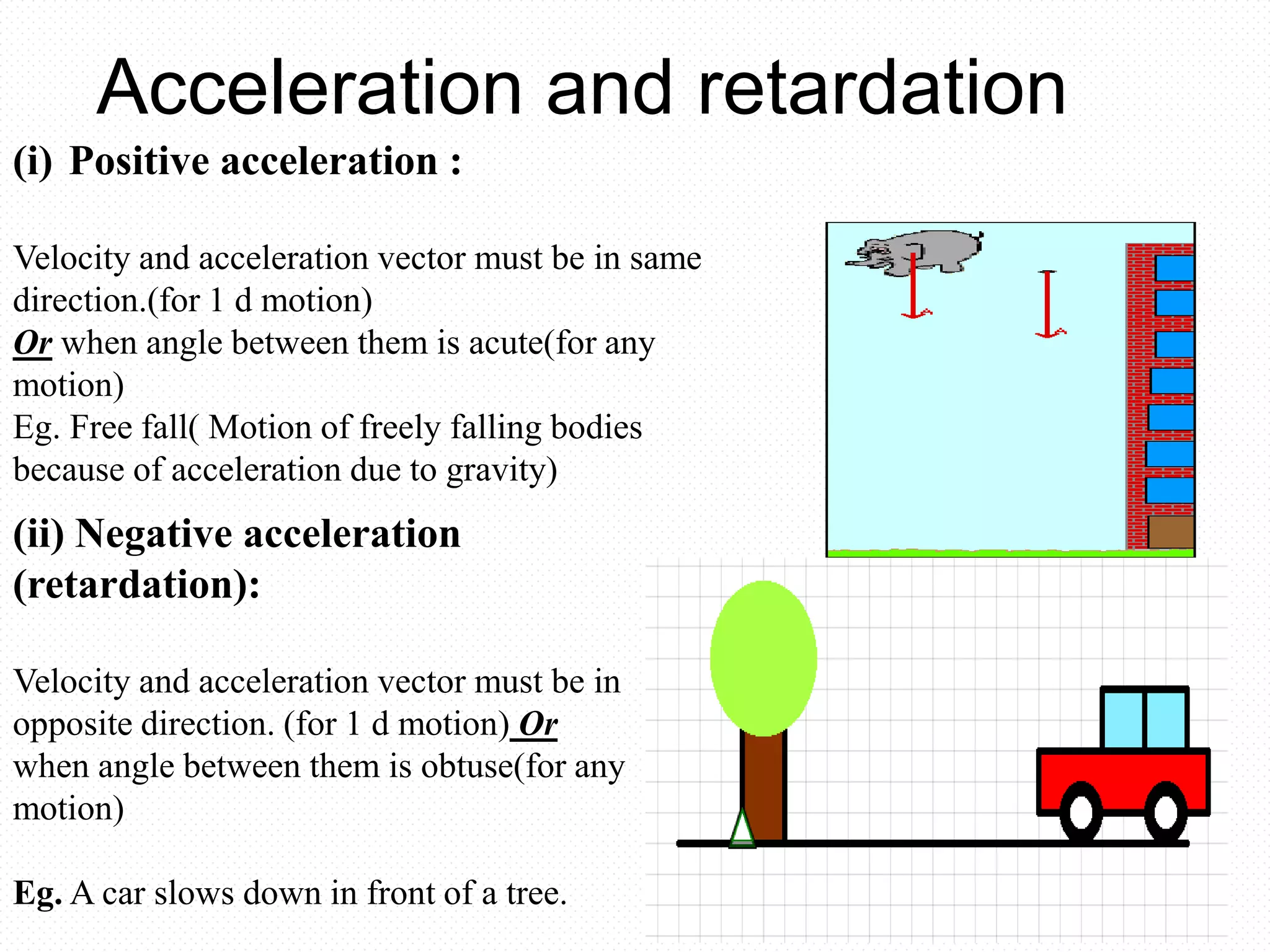
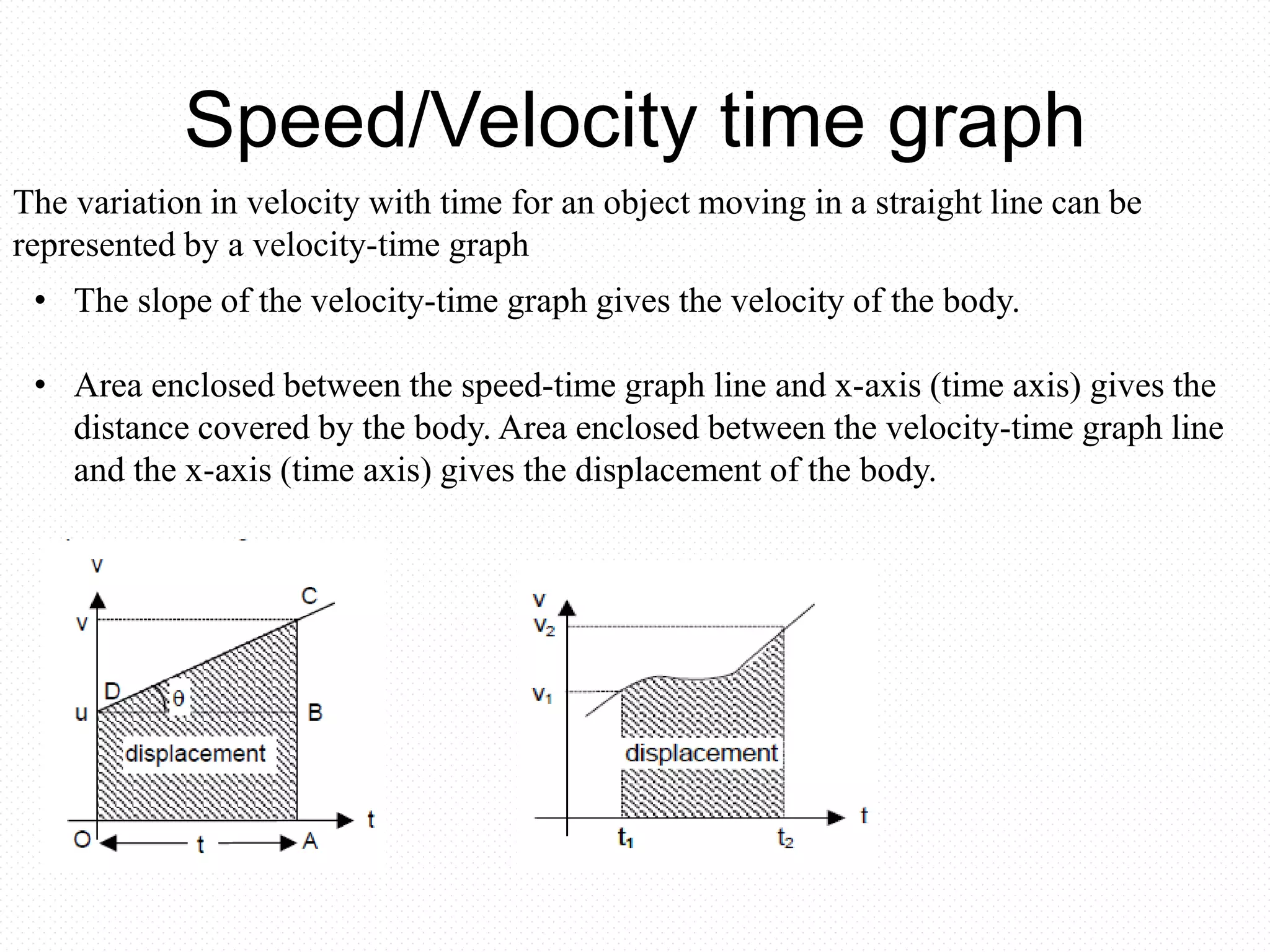
Here are the key points about rate of change of velocity:
- Rate of change of velocity is also known as acceleration.
- Acceleration is a vector quantity which indicates the rate at which the velocity of an object is changing.
- The SI unit of acceleration is meter per second squared (m/s2).
- If an object's velocity is increasing with time, it has a positive acceleration. If velocity is decreasing with time, acceleration is negative.
- Acceleration can be caused by a change in the object's speed, direction of motion, or both.
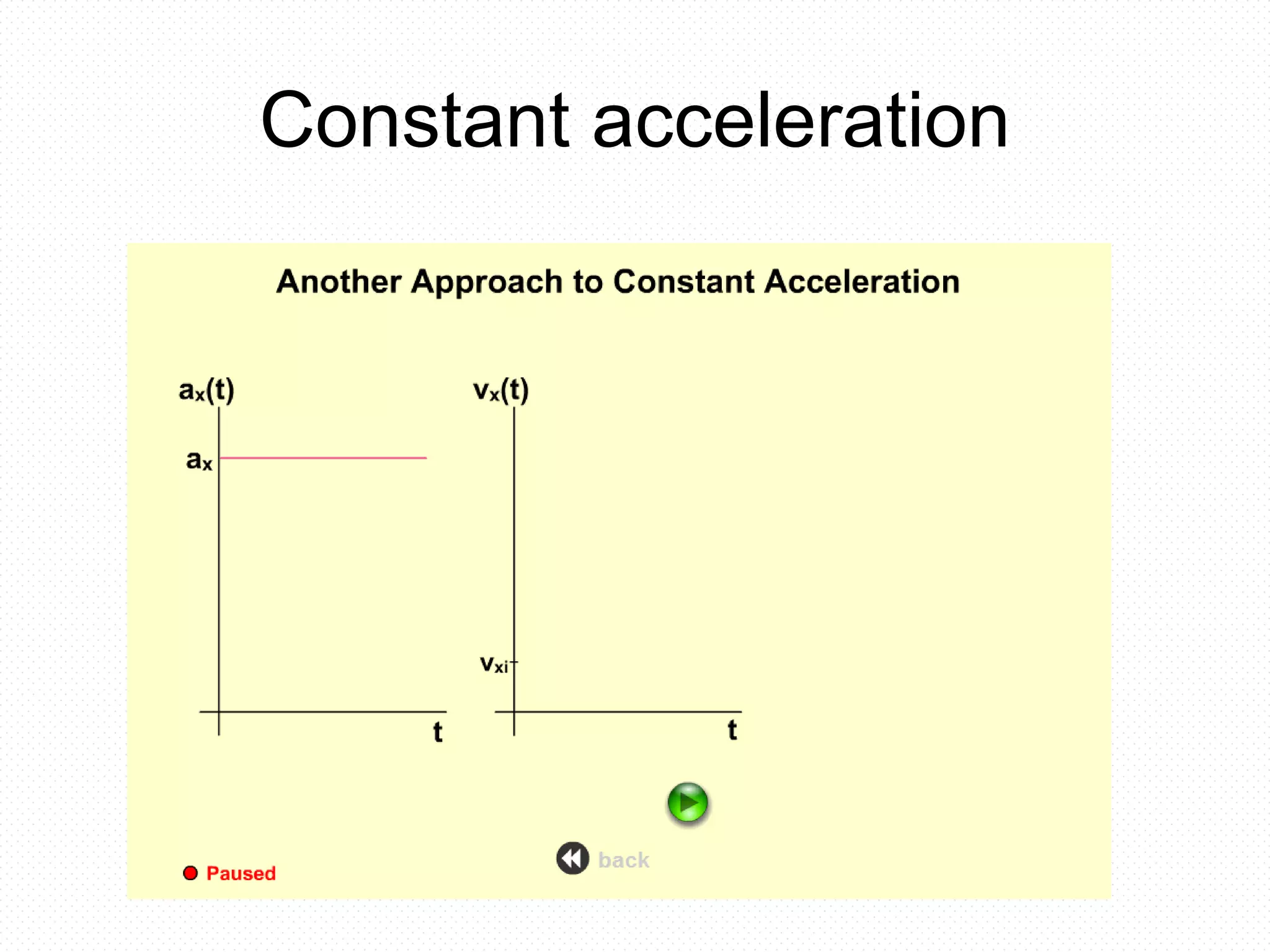
- Constant acceleration means the rate of change of velocity remains the same over time. This results in a linear relationship between velocity and time

































![Speed
Different objects have different
speeds
Speed : Rate of change of distance covered per unit time is called speed.
(i) It is a scalar quantity having symbol .
(ii) Dimension : [M0L1T–1]
(iii) Unit : metre/second (S.I.), cm/second (C.G.S.)](https://image.slidesharecdn.com/kinematicsclass-160301170659/75/Kinematics-class-34-2048.jpg)







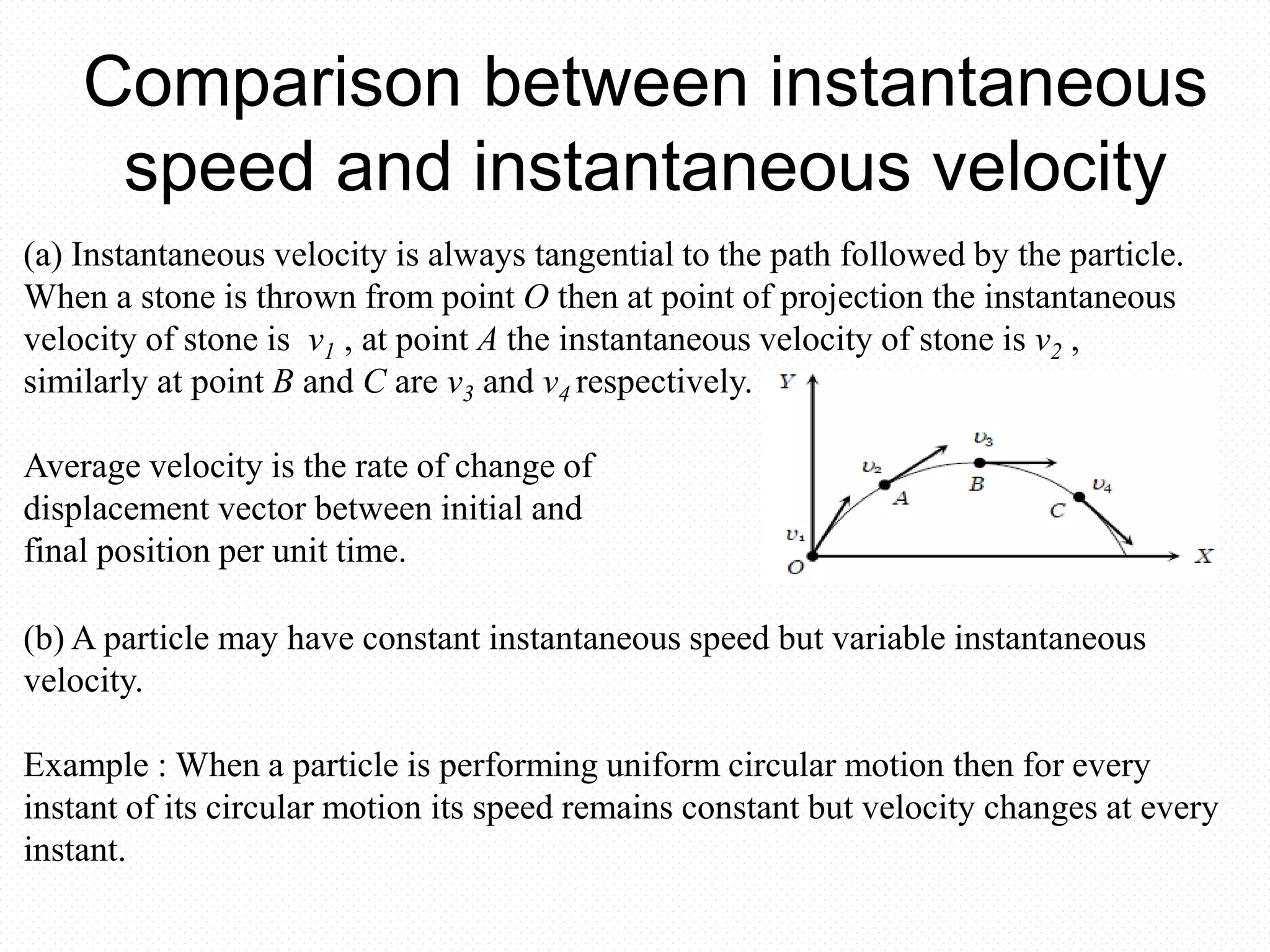

![Comparison between average
speed and average velocity
(a) Average speed is scalar while average velocity is a vector both having
same units (m/s) and dimensions [LT ] 1.
(b) Average speed or velocity depends on time interval over which it is defined.
(c) For a given time interval average velocity is single valued while average
speed can have many values depending on path followed.](https://image.slidesharecdn.com/kinematicsclass-160301170659/75/Kinematics-class-44-2048.jpg)


































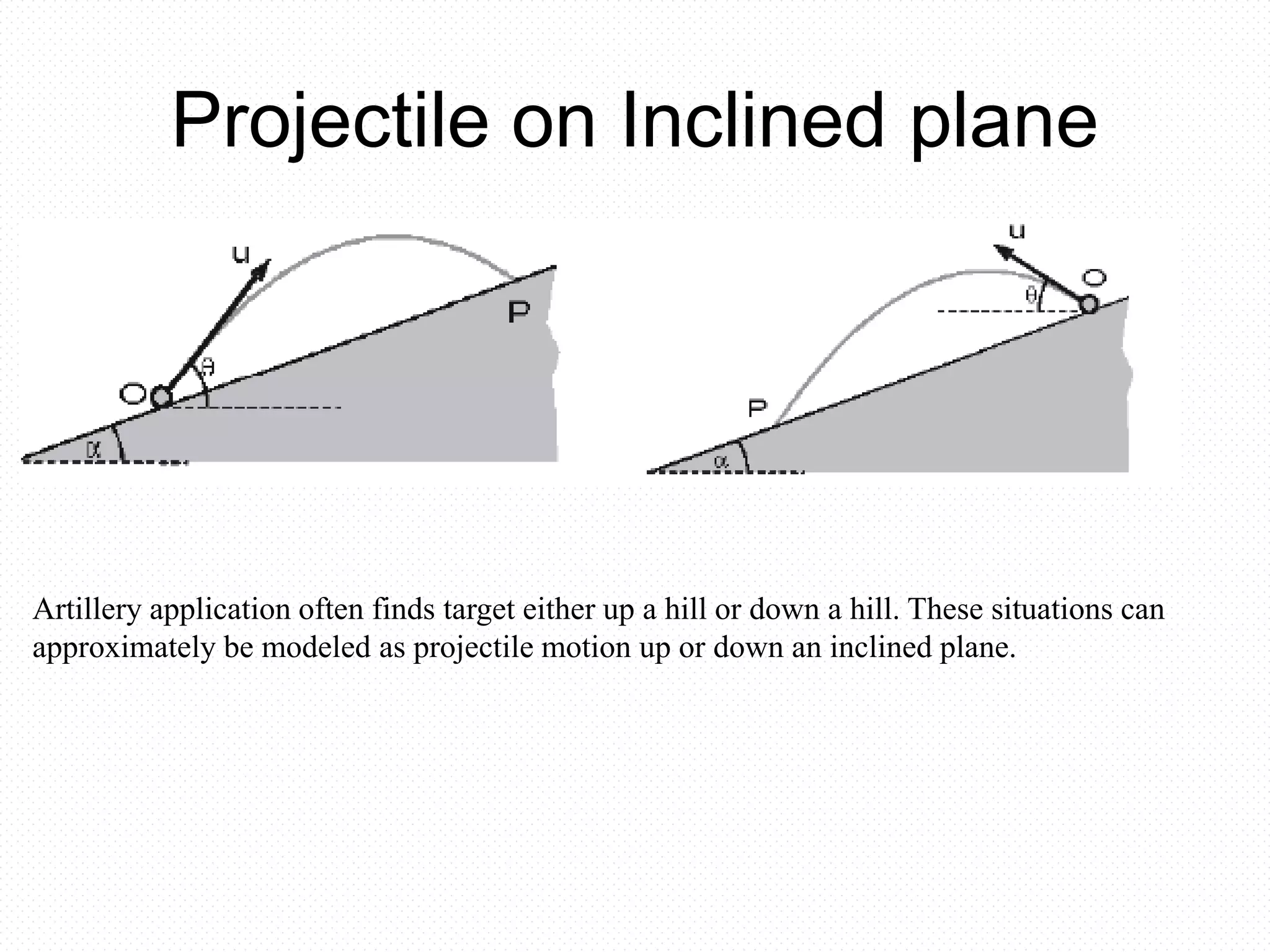
![PROJECTILE THROWN AT AN
ANGLE WITH HORIZONTAL
Y
uy = u sin
u
ux = u cos
ux
R
H
X
jsinuicosuu
juiuu yx
The X axis is parallel to the horizontal. Y axis is parallel to the vertical and the u lies in the plane X -
Y. The constant acceleration a is given as
jaiaa yx
Where ax = 0 [ as there is no acceleration along the X - axis].
ay = -g [the acceleration is downward and equal to g].
Now velocity after time t is given as.
vtx = ux + axt = u cos (as ax = 0)
vty = uy + ayt = usin - gt
jˆviˆvv yx
jˆ)gtsinu(iˆcosuv t
The direction of v
with the x axis is given by
x
y1
v
v
tan
Velocity of projectile](https://image.slidesharecdn.com/kinematicsclass-160301170659/75/Kinematics-class-83-2048.jpg)