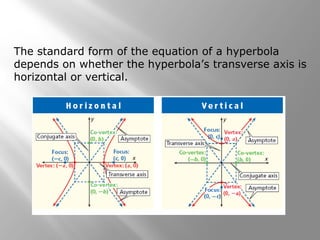
This document discusses hyperbolas, including: 1) Hyperbolas are defined as sets of points where the difference between the distances to two fixed points (foci) is a constant. They can be graphed using the standard form equation. 2) Hyperbolas have two branches, two axes of symmetry, vertices, co-vertices, and asymptotes. The standard form equation depends on whether the transverse axis is horizontal or vertical. 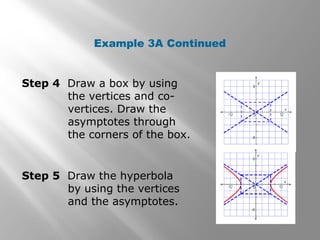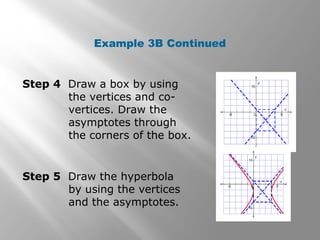3) Examples show how to write the standard form equation, find vertices/co-vertices/asymptotes, and graph hyperbolas. Parameters like the center, foci and axes can change the graph of the hyperbola.

1. UNIT 13.5 HYPERBOLASUNIT 13.5 HYPERBOLAS

2. Warm Up
Multiply both sides of each equation by
the least common multiple to eliminate
the denominators.
4x
2
– 9y
2
= 361.
x
2
9
– = 1y
2
4
2.
y
2
25
– = 1x
2
16
16y
2
– 25x
2
= 400

3. Write the standard equation for a
hyperbola.
Graph a hyperbola, and identify its
center, vertices, co-vertices, foci, and
asymptotes.
Objectives

4. hyperbola
focus of a hyperbola
branch of a hyperbola
transverse axis
vertices of a hyperbola
conjugate axis
co-vertices of a hyperbola
Vocabulary

5. What would happen if you pulled the two foci of an
ellipse so far apart that they moved outside the
ellipse? The result would be a hyperbola, another
conic section.
A hyperbola is a set of points P(x, y) in a plane such
that the difference of the distances from P to fixed
points F1 and F2, the foci, is constant. For a hyperbola,
d = |PF1 – PF2 |, where d is the constant difference. You
can use the distance formula to find the equation of a
hyperbola.

6. Find the constant difference for a hyperbola with foci
F1 (–8, 0) and F2 (8, 0) and the point on the hyperbola (8, 30).
Example 1: Using the Distance Formula to Find the
Constant Difference of a Hyperbola
Definition of the constant difference
of a hyperbola.
d = |PF1 – PF2 |
Distance Formula
Substitute.
Simplify.
d = 4
The constant difference is 4.

7. Find the constant difference for a hyperbola with foci
F1 (0, –10) and F2 (0, 10) and the point on the hyperbola (6, 7.5).
Check It Out! Example 1

8. As the graphs in the following table show, a hyperbola
contains two symmetrical parts called branches.
A hyperbola also has two axes of symmetry. The
transverse axis of symmetry contains the vertices
and, if it were extended, the foci of the hyperbola. The
vertices of a hyperbola are the endpoints of the
transverse axis.
The conjugate axis of symmetry separates the two
branches of the hyperbola. The co-vertices of a
hyperbola are the endpoints of the conjugate axis.
The transverse axis is not always longer than the
conjugate axis.

9. The standard form of the equation of a hyperbola
depends on whether the hyperbola’s transverse axis is
horizontal or vertical.

10. The values a, b, and c, are related by the equation c2
= a
2
+ b
2
. Also note that the length of the transverse
axis is 2a and the length of the conjugate is 2b.

11. Write an equation in standard form for each
hyperbola.
Example 2A: Writing Equations of Hyperbolas
Step 1 Identify the form of
the equation.
The graph opens horizontally, so the equation
will be in the form of .x
2
a
2
– = 1y
2
b
2

12. Example 2A Continued
Step 2 Identify the center and the vertices.
The center of the graph is (0, 0), and the
vertices are (–6, 0) and (6, 0), and the co-
vertices are (0, –6), and (0, 6). So a = 6, and
b = 6.
Step 3 Write the equation.
x
2
36
– = 1.y
2
36
Because a = 6 and b = 6, the equation of the
graph is
x
2
62
– = 1, ory
2
62

13. Example 2B: Writing Equations of Hyperbolas
The hyperbola with center at the origin,
vertex (4, 0), and focus (10, 0).
Step 1 Because the vertex and the focus are on the
horizontal axis, the transverse axis is
horizontal and the equation is in the form
.x
2
a
2
– = 1y
2
b
2
Write an equation in standard form for each
hyperbola.

14. Example 2B Continued
Step 2 Use a = 4 and c = 10; Use c2
= a2
+ b2
to
solve for b
2
.
102
= 4
2
+ b
2
84 = b
2
Substitute 10 for c, and 4 for a.
Step 3 The equation of the hyperbola is .x
2
16
– = 1y
2
84

15. Write an equation in standard form for each
hyperbola.
Vertex (0, 9), co-vertex (7, 0)
Check It Out! Example 2a

16. Vertex (8, 0), focus (10, 0)
Check It Out! Example 2b
Write an equation in standard form for each
hyperbola.

17. As with circles and ellipses, hyperbolas do not have
to be centered at the origin.

18. Example 3A: Graphing a Hyperbola
Find the vertices, co-vertices, and asymptotes of
each hyperbola, and then graph.
Step 1 The equation is in the form
so the transverse axis is horizontal
with center (0, 0).
x
2
a
2
– = 1y
2
b
2
x
2
49
– = 1y
2
9

19. Example 3A Continued
Step 2 Because a = 7 and b = 3, the vertices are
(–7, 0) and (7, 0) and the co-vertices are
(0, –3) and (0, 3).
3
7
Step 3 The equations of the asymptotes are
y = x and y = – x.
3
7

20. Example 3A Continued
Step 4 Draw a box by using
the vertices and co-
vertices. Draw the
asymptotes through
the corners of the box.
Step 5 Draw the hyperbola
by using the vertices
and the asymptotes.

21. Find the vertices, co-vertices, and asymptotes of
each hyperbola, and then graph.
(x – 3)
2
9
– = 1(y + 5)
2
49
Step 1 The equation is in the form
, so the
transverse axis is horizontal with
center (3, –5).
(x – h)
2
a
2
– = 1(y – k)
2
b
2
Example 3B: Graphing a Hyperbola

22. Example 3B Continued
Step 2 Because a = 3 and b =7,
the vertices are (h + a, k) and (h – a, k)
(0, –5) and (6, –5)
the co-vertices are (h, k + b) and (h, k – b)
(3, –12) and (3, 2) .
Step 3 The equations of the asymptotes are
y + 5 = (x – 3) and y = – (x – 3).
7
3
7
3

23. Example 3B Continued
Step 4 Draw a box by using
the vertices and co-
vertices. Draw the
asymptotes through
the corners of the box.
Step 5 Draw the hyperbola
by using the vertices
and the asymptotes.

24. Find the vertices, co-vertices, and asymptotes of
each hyperbola, and then graph.
x
2
16
– = 1y
2
36
Check It Out! Example 3a

25. Notice that as the parameters change, the graph
of the hyperbola is transformed.

26. All rights belong to their respective owners.
Copyright Disclaimer Under Section 107 of
the Copyright Act 1976, allowance is made
for "fair use" for purposes such as criticism,
comment, news reporting, TEACHING,
scholarship, and research.
Fair use is a use permitted by copyright
statute that might otherwise be infringing.
Non-profit, EDUCATIONAL or personal use
tips the balance in favor of fair use.