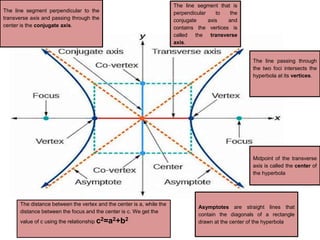
This document defines key terms related to hyperbolas and provides examples of finding the standard form of the equation of a hyperbola given certain properties. It defines a hyperbola as a set of points where the absolute difference between the distances to two fixed points (foci) is a constant. It provides examples of identifying the vertices, foci, asymptotes, and standard form of the equation from information given, such as the coordinates of vertices and foci or the asymptotes.

2. •Define a hyperbola.
•Determine the standard
form of equation of a
hyperbola.

3. • State the definition of
hyperbola.
• Recognize the parts of the
hyperbola given their
corresponding description.

4. • Identify the value of the parts of
the hyperbola given its equation
in standard form.
• Find the equation of the
hyperbola in standard form
determined by the given
conditions.

6. The difference of the distances
between the foci and a point
on the hyperbola is fixed.

7. The set of all points such that the
absolute value of the difference of
the distance of each point from
two fixed points is a constant.

9. The line passing through
the two foci intersects the
hyperbola at its vertices.
The line segment that is
perpendicular to the
conjugate axis and
contains the vertices is
called the transverse
axis.
Midpoint of the transverse
axis is called the center of
the hyperbola
The line segment perpendicular to the
transverse axis and passing through the
center is the conjugate axis.
Asymptotes are straight lines that
contain the diagonals of a rectangle
drawn at the center of the hyperbola
The distance between the vertex and the center is a, while the
distance between the focus and the center is c. We get the
value of c using the relationship c2=a2+b2

11. Horizontal Vertical
Equation 𝑥2
𝑎2
−
𝑦2
𝑏2
= 1
𝑦2
𝑎2
−
𝑥2
𝑏2
= 1
Center (0,0) (0,0)
Vertices (V) (± a , 0) (0, ± a)
End of conjugate axis (ECA) (0 ,± b) (± b, 0)
Foci ( c ) C 𝑎2 + 𝑏2
(±c , 0)
C 𝑎2 + 𝑏2
(0, ±c)
Length of the latus Rectum 2𝑏2
𝑎
2𝑏2
𝑎
Asymptotes y =±
𝑏
𝑎
𝑥 y =±
𝑎
𝑏
𝑥
Length of the transverse axis
(LTA)
2a 2a
Length of the conjugate axis 2b 2b
Graph

12. Equation
Transverse
Axis
Vertices Foci
Ends of
Conjugate
Axis
𝒙𝟐
𝒂𝟐
−
𝒚𝟐
𝒃𝟐
= 𝟏
c>a
c= 𝑎2 + 𝑏2
Horizontal (±a,0) (±c,0)
𝒚𝟐
𝒂𝟐
−
𝒙𝟐
𝒃𝟐
= 𝟏
c>a
c= 𝑎2 + 𝑏2
(0,±a) (0,±c)
Asymptotes
𝑦 = ±
𝑏
𝑎
𝑥
𝑦 = ±
𝑎
𝑏
𝑥
Equation
Vertical
(0,±b)
(±b,0)

13. Identify the coordinates of the
vertices , foci, ends of conjugate
axis, and equation of the
asymptotes.
𝒙𝟐
𝟏𝟔
−
𝒚𝟐
𝟒
= 𝟏

14. Identify the values of
a and b from the standard
equation.
𝑥2
𝑎2 −
𝑦2
𝑏2 = 1
𝑥2
16
−
𝑦2
4
= 1
a2=16 b2=4
a=±4 b=±2

15. Determine the
vertices.
a=distance between the vertex and
the center which is at the origin
Horizontal Transverse Axis
Vertices at (‒4,0) and (4,0).

16. Determine the
ends of the conjugate axis.
b=distance from the center to the
endpoints of the conjugate axis
(0,‒2) and (0,2)

17. Use the relationship c2=a2+b2
to determine the foci and substitute the
values of a and b into the equation.
c2=a2+b2
c2=16+4
c2=20
c=± 20
c=±2 5≈4.5
(4.5,0) and (‒4.5, 0)

18. To determine the
equations of the asymptotes,
substitute the values of a and b
to the equation y=±
𝑏
𝑎
x.
y=±
𝑏
𝑎
x y=±
2
4
x y=±
1
2
x
y=
𝟏
𝟐
x and y= ‒
𝟏
𝟐
x

20. Find the standard form of the
equation of the hyperbola
with center at the origin, foci
(±7,0) , and vertices (±5,0).

21. Determine the value of
a.
Since a is the distance between the
center (0,0) and the vertex (5,0),
a=5
Furthermore, since the vertices lie
on the x-axis, the hyperbola has a
horizontal transverse axis.

22. Determine the value
of c.
Since c is the distance between
the center (0,0) and the focus (7,0),
c=7

23. Determine the value of b.
Using the relationship c2=a2+b2, it
follows that
b2=c2‒a2
b2=72‒52
b2=49‒25
b2=24
b= 24
b= 4 • 6
b=±2 𝟔≈±4.9

24. Determine the standard
form of the equation of the hyperbola.
Since the hyperbola has a horizontal
transverse axis, we use the form
𝑥2
𝑎2 ‒
𝑦2
𝑏2=1.
Upon substituting the values, we
get
𝒙𝟐
𝟓𝟐 ‒
𝒚𝟐
( 𝟐𝟒)𝟐 = 1.

25. Simplify the standard form
of the equation of the hyperbola.
𝑥2
25
‒
𝑦2
24
= 1
Therefore, the standard form of the
equation of the hyperbola is
𝒙𝟐
𝟐𝟓
‒
𝒚𝟐
𝟐𝟒
= 1

27. Find the standard form of the
equation of the hyperbola
having vertices (0, ±10) and
asymptotes y=±5x.

28. Determine the center
of the hyperbola by getting the
midpoint between the vertices.
Midpoint =
0+0
2
,
10+(−10)
2
=(0,0)
Thus, the center of the hyperbola
is (0,0)

29. Determine the value
of a.
Since a is the distance from the
center to the vertex, then a=10.
Furthermore, since the vertices
lie on the y-axis, the hyperbola has a
vertical transverse axis.

30. Determine the slopes
of the asymptotes.
Since the hyperbola has a vertical
transverse axis, asymptotes are of
the form y=±
𝑎
𝑏
x. thus, y= ±5x.
Therefore the slopes are m1= 5
and m2= ‒5.

31. Determine the value of
b.
Since 5=
𝑎
𝑏
, then b=
𝑎
5
Thus, b=
10
5
=2

32. Determine the standard form of the
equation of the hyperbola.
Since the hyperbola has a vertical transverse axis with
center (0,0) , we use the standard form of the equation
𝑦2
𝑎2 ‒
𝑥2
𝑏2 = 1
Substituting the values, we get
𝑦2
(10)2 ‒
𝑥2
(2)2 = 1
or
𝑦2
100
‒
𝑥2
4
= 1
Therefore, the standard form of the equation of the
hyperbola is
𝒚𝟐
𝟏𝟎𝟎
‒
𝒙𝟐
𝟒
= 𝟏