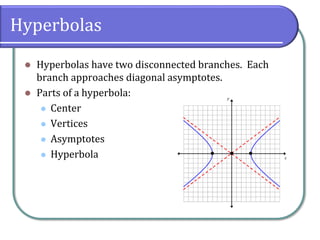
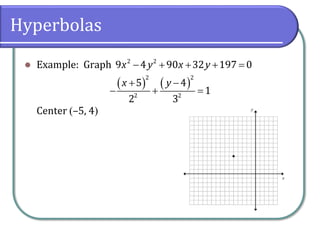
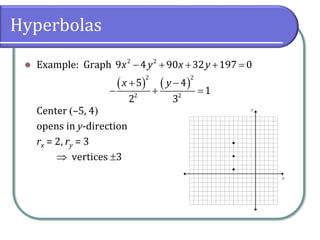
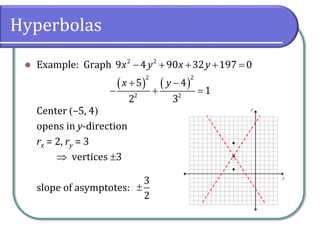
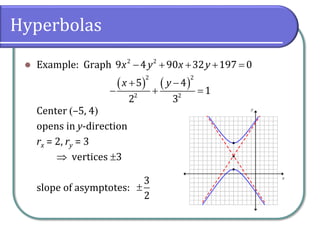
The document covers the properties and equations of hyperbolas in analytic geometry, detailing how to identify key features such as center, vertices, asymptotes, and foci from hyperbolic equations. It explains the relationship between eccentricity and the shape of hyperbolas, emphasizing that their eccentricity is always greater than 1. The document also includes example problems for graphing hyperbolas and calculating their eccentricity.

1. 10.3 Hyperbolas
Chapter 10 Analytic Geometry

2. Concepts and Objectives
⚫ Hyperbolas
⚫ Identify equations of hyperbolas
⚫ From the equation, identify the center, direction of
opening, vertices, x-radius, y-radius, slope of the
asymptotes, and foci
⚫ Sketch the hyperbola
⚫ Determine the eccentricity
⚫ Write the equation of the hyperbola

3. Hyperbolas
⚫ Hyperbolas have two disconnected branches. Each
branch approaches diagonal asymptotes.
⚫ Parts of a hyperbola:
⚫ Center
⚫ Vertices
⚫ Asymptotes
⚫ Hyperbola • ••

4. Hyperbolas
⚫ The general equation of a hyperbola is
or
⚫ The hyperbola opens in whichever direction has the
positive term (x-direction if x is positive, y-direction if y
is positive).
⚫ The slope of the asymptotes is always .
⚫ The vertices are rx or ry from the center, whichever is
positive. a is the positive term radius, b is the negative
term radius.
  − −
− =    
   
22
1
x y
x h y k
r r
  − −
− + =    
   
22
1
x y
x h y k
r r
 y
x
r
r

5. Hyperbolas
⚫ Example: Graph − + + + =2 2
9 4 90 32 197 0x y x y

6. Hyperbolas
⚫ Example: Graph − + + + =2 2
9 4 90 32 197 0x y x y
( ) ( ) ( ) ( )++ − =+ +−− −22 2 22 2
9 10 8 1975 9 54 4 4 4x x y y
Notice that the
negative sign has
been factored as
well!
Remember to
distribute the
negative sign!

7. Hyperbolas
⚫ Example: Graph − + + + =2 2
9 4 90 32 197 0x y x y
( ) ( ) ( ) ( )++ − =+ +−− −22 2 22 2
9 10 8 1975 9 54 4 4 4x x y y
( ) ( )+ − − = −
2 2
9 64 45 3x yNotice that the
negative sign has
been factored as
well!
Remember to
distribute the
negative sign!

8. Hyperbolas
⚫ Example: Graph − + + + =2 2
9 4 90 32 197 0x y x y
( ) ( ) ( ) ( )++ − =+ +−− −22 2 22 2
9 10 8 1975 9 54 4 4 4x x y y
( ) ( )+ − −
− =
− − −
2 2
9 5 4 4 36
36 36 36
x yNotice that the
negative sign has
been factored as
well!
Remember to
distribute the
negative sign!

9. Hyperbolas
⚫ Example: Graph − + + + =2 2
9 4 90 32 197 0x y x y
( ) ( ) ( ) ( )++ − =+ +−− −22 2 22 2
9 10 8 1975 9 54 4 4 4x x y y
( ) ( )+ − −
− =
− − −
2 2
9 5 4 4 36
36 36 36
x y
( ) ( )+ −
− + =
2 2
5 4
1
4 9
x y
Notice that the
negative sign has
been factored as
well!
Remember to
distribute the
negative sign!

10. Hyperbolas
⚫ Example: Graph − + + + =2 2
9 4 90 32 197 0x y x y
( ) ( ) ( ) ( )++ − =+ +−− −22 2 22 2
9 10 8 1975 9 54 4 4 4x x y y
( ) ( )+ − −
− =
− − −
2 2
9 5 4 4 36
36 36 36
x y
( ) ( )+ −
− + =
2 2
5 4
1
4 9
x y
( ) ( )+ −
− + =
2 2
2 2
5 4
1
2 3
x y
Notice that the
negative sign has
been factored as
well!
Remember to
distribute the
negative sign!

11. Hyperbolas
⚫ Example: Graph
Center (–5, 4)
− + + + =2 2
9 4 90 32 197 0x y x y
( ) ( )+ −
− + =
2 2
2 2
5 4
1
2 3
x y

12. Hyperbolas
⚫ Example: Graph
Center (–5, 4)
opens in y-direction
rx = 2, ry = 3
 vertices 3
− + + + =2 2
9 4 90 32 197 0x y x y
( ) ( )+ −
− + =
2 2
2 2
5 4
1
2 3
x y

13. Hyperbolas
⚫ Example: Graph
Center (–5, 4)
opens in y-direction
rx = 2, ry = 3
 vertices 3
slope of asymptotes:
− + + + =2 2
9 4 90 32 197 0x y x y
( ) ( )+ −
− + =
2 2
2 2
5 4
1
2 3
x y

3
2

14. Hyperbolas
⚫ Example: Graph
Center (–5, 4)
opens in y-direction
rx = 2, ry = 3
 vertices 3
slope of asymptotes:
− + + + =2 2
9 4 90 32 197 0x y x y
( ) ( )+ −
− + =
2 2
2 2
5 4
1
2 3
x y

3
2

15. Focal Length
⚫ In an ellipse, the sum of the distances from a point on the
ellipse to the two foci is constant, but in a hyperbola, it’s
the difference between the distances that is constant.
⚫ To find the focal radius, we can use the Pythagorean
Theorem.
⚫ Notice that c > a for the
hyperbola. a
b
c
•
= +2 2 2
c a b

16. Eccentricity
⚫ Like the ellipse, the eccentricity of the hyperbola
determines the basic shape, and like the ellipse, the
eccentricity of the hyperbola is
⚫ In an ellipse, e will always be between 0 and 1, but in a
hyperbola, e will always be greater than 1.
=
c
e
a

17. Eccentricity
⚫ Example: Find the eccentricity of the hyperbola
− =
2 2
1
9 4
x y

18. Eccentricity
⚫ Example: Find the eccentricity of the hyperbola
a = 3, b = 2
− =
2 2
1
9 4
x y
− =
2 2
2 2
1
3 2
x y
= +2 2 2
3 2c
= + =9 4 13
= 13c
= 
13
1.2
3
e

19. Eccentricity
⚫ Example: Write the equation of the hyperbola with
eccentricity 2 and foci at (–9, 5) and (–3, 5).

20. Eccentricity
⚫ Example: Write the equation of the hyperbola with
eccentricity 2 and foci at (–9, 5) and (–3, 5).
The foci’s coordinates tell us that the hyperbola opens in
the x-direction, that the center is at (–6, 5), and that c = 3.
=
3
2
a
 =1.5a
= − =2
9 2.25 6.75b
=2
2.25a
( ) ( )+ −
− =
2 2
6 5
1
2.25 6.75
x y

21. Classwork
⚫ College Algebra
⚫ Page 978: 10-22 (even), page 968: 16-28 (even),
page 959: 52-56 (even)