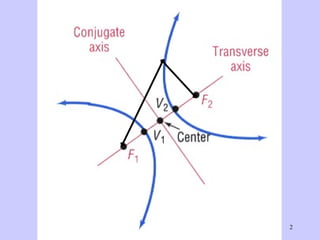
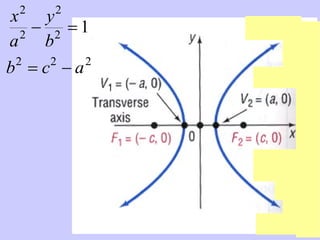
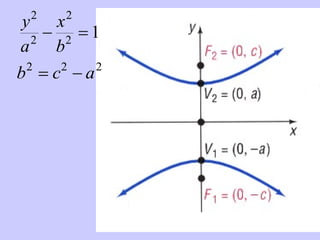
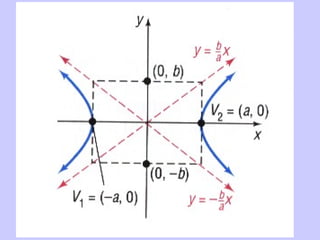
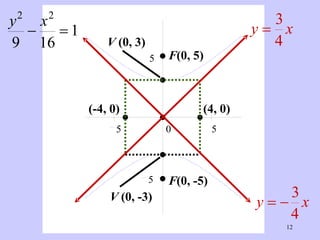
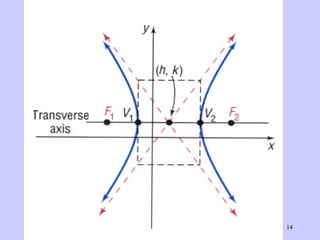
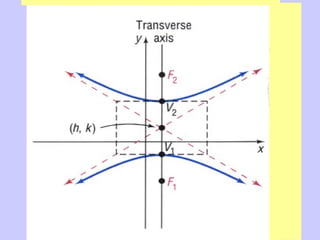
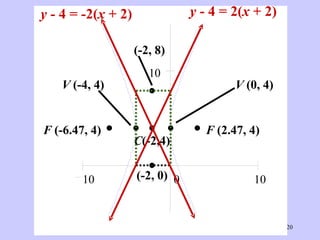
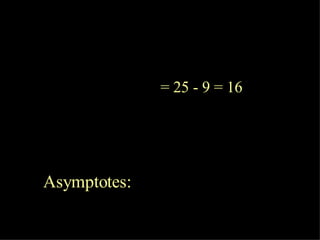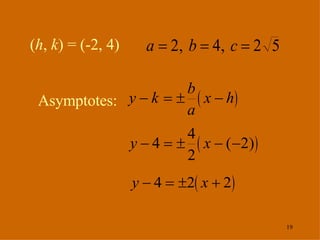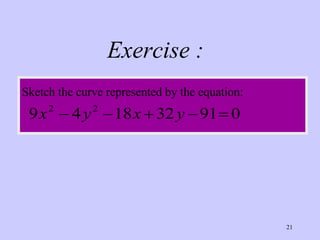The document discusses hyperbolas and their key properties. It defines a hyperbola as the set of points where the difference between the distances to two fixed points (foci) is a constant. It provides the equations of hyperbolas with the foci and vertices in various positions. It gives examples of finding the equation, vertices, foci, and asymptotes of hyperbolas satisfying given conditions. It also discusses hyperbolas with transverse axes parallel to the x- or y-axis.

1. A hyperbola is the collection of points in the plane the difference of whose distances from two fixed points, called the foci , is a constant. HYPERBOLA

3. Theorem Equation of a Hyberbola; Center at (0, 0); Foci at ( + c , 0); Vertices at ( + a , 0); Transverse Axis along the x -Axis An equation of the hyperbola with center at (0, 0), foci at ( - c , 0) and ( c , 0), and vertices at ( - a , 0) and ( a, 0) is The transverse axis is the x -axis.

5. Theorem Equation of a Hyberbola; Center at (0, 0); Foci at ( 0, + c ); Vertices at (0, + a ); Transverse Axis along the y -Axis An equation of the hyperbola with center at (0, 0), foci at (0, - c ) and (0, c ), and vertices at (0, - a ) and (0, a ) is The transverse axis is the y -axis.

7. Theorem Asymptotes of a Hyperbola The hyperbola has the two oblique asymptotes

9. Theorem Asymptotes of a Hyperbola The hyperbola has the two oblique asymptotes

10. Find an equation of a hyperbola with center at the origin, one focus at (0, 5) and one vertex at (0, -3). Determine the oblique asymptotes. Graph the equation by hand and using a graphing utility. Center: (0, 0) Focus: (0, 5) = (0, c ) Vertex: (0, -3) = (0, - a ) Transverse axis is the y -axis, thus equation is of the form

11. = 25 - 9 = 16 Asymptotes:

12. V (0, 3) V (0, -3) (4, 0) (-4, 0) F (0, 5) F (0, -5)

13. Hyperbola with Transverse Axis Parallel to the x -Axis; Center at ( h , k ) where b 2 = c 2 - a 2 .

15. Hyperbola with Transverse Axis Parallel to the y -Axis; Center at ( h , k ) where b 2 = c 2 - a 2 .

17. Find the center, transverse axis, vertices, foci, and asymptotes of

18. Center: ( h , k ) = (-2, 4) Transverse axis parallel to x -axis. Vertices: ( h + a , k ) = (-2 + 2, 4) or (-4, 4) and (0, 4)

19. Asymptotes: ( h , k ) = (-2, 4)

20. C (-2,4) V (-4, 4) V (0, 4) F (2.47, 4) F (-6.47, 4) (-2, 8) (-2, 0) y - 4 = -2( x + 2) y - 4 = 2( x + 2)

21. Sketch the curve represented by the equation: Exercise :

22. Solution:

23. Note:- To understand what this curve might look like, we have to work towards a standard form. This is best accomplished by completing the square in the x terms and in the y terms. From this, we see that the curve is a hyperbola centered at (1, 4). When y = 4 we have:

24. So, Thus, or Therefore, (3, 4) and are both on the curve. The asymptotes are the lines and and they pass through the centre (1, 4).