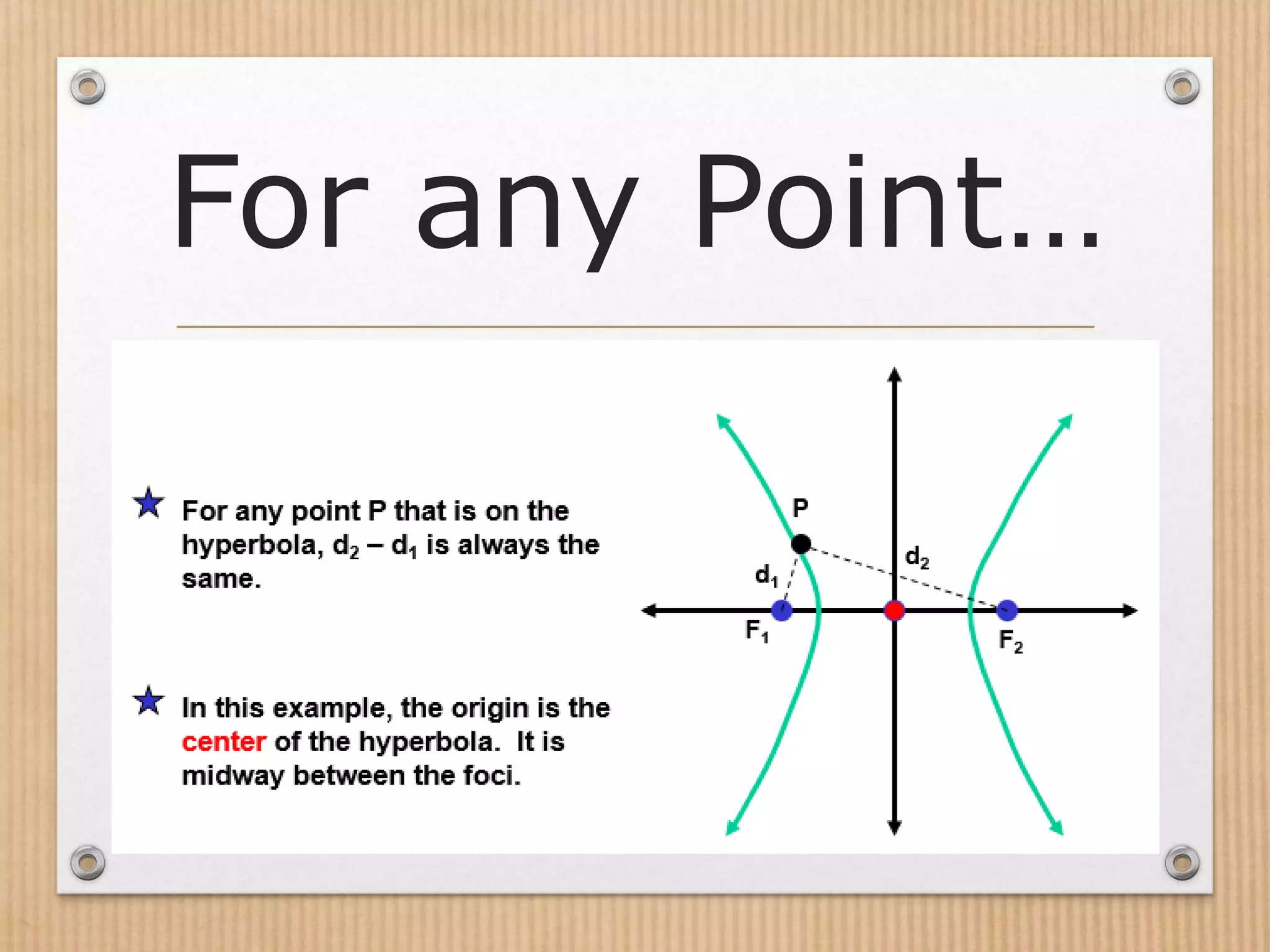
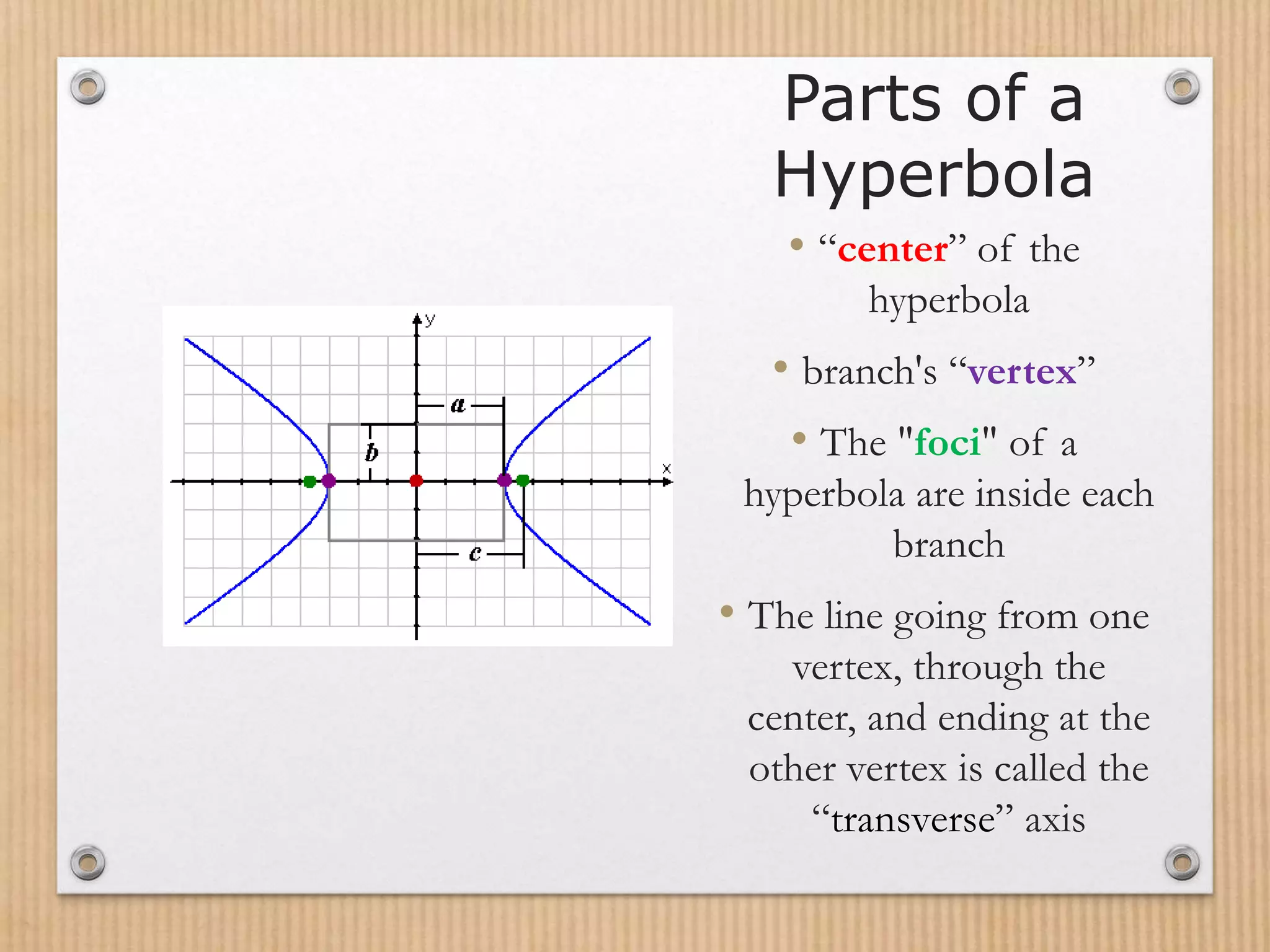
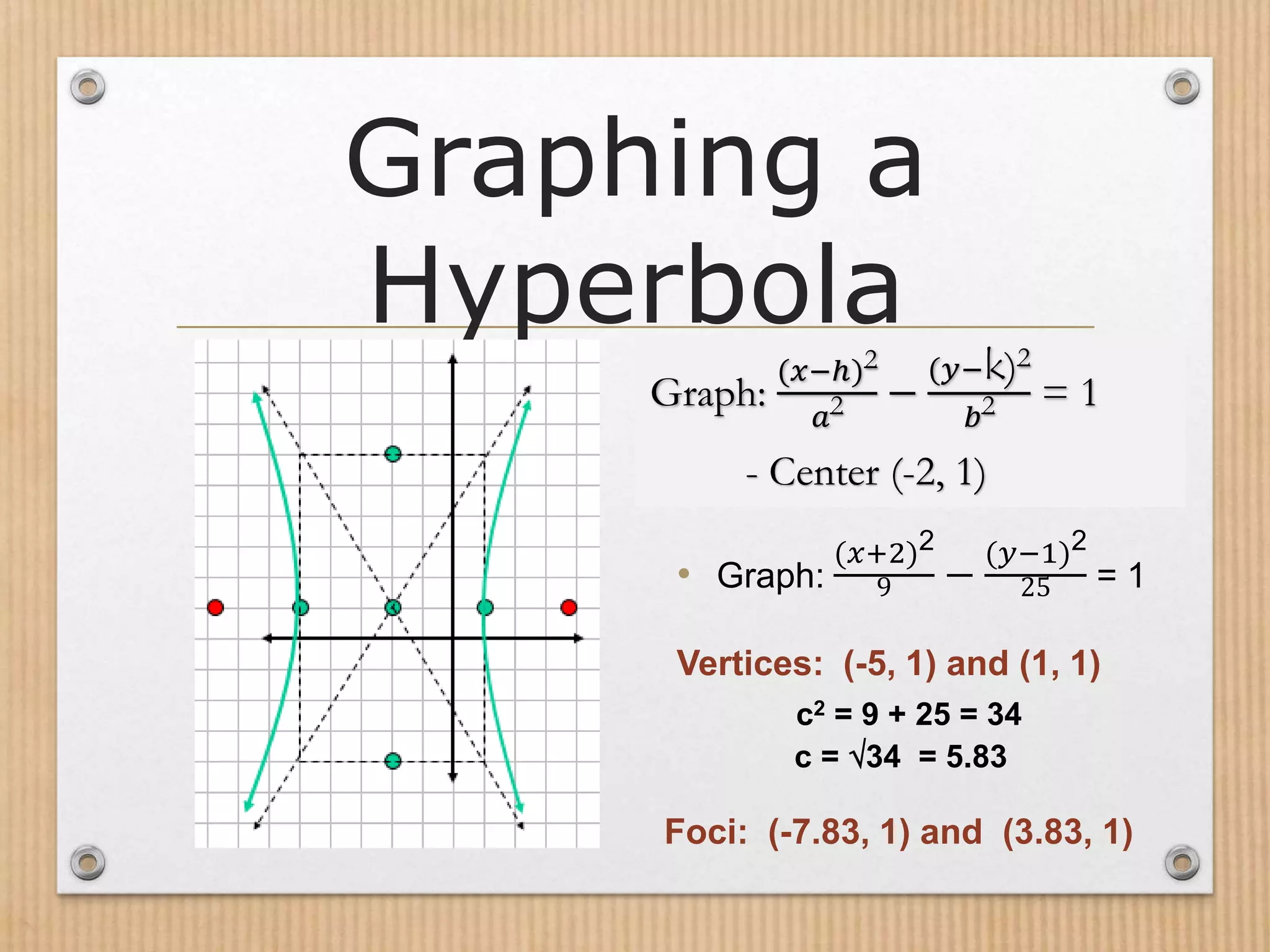
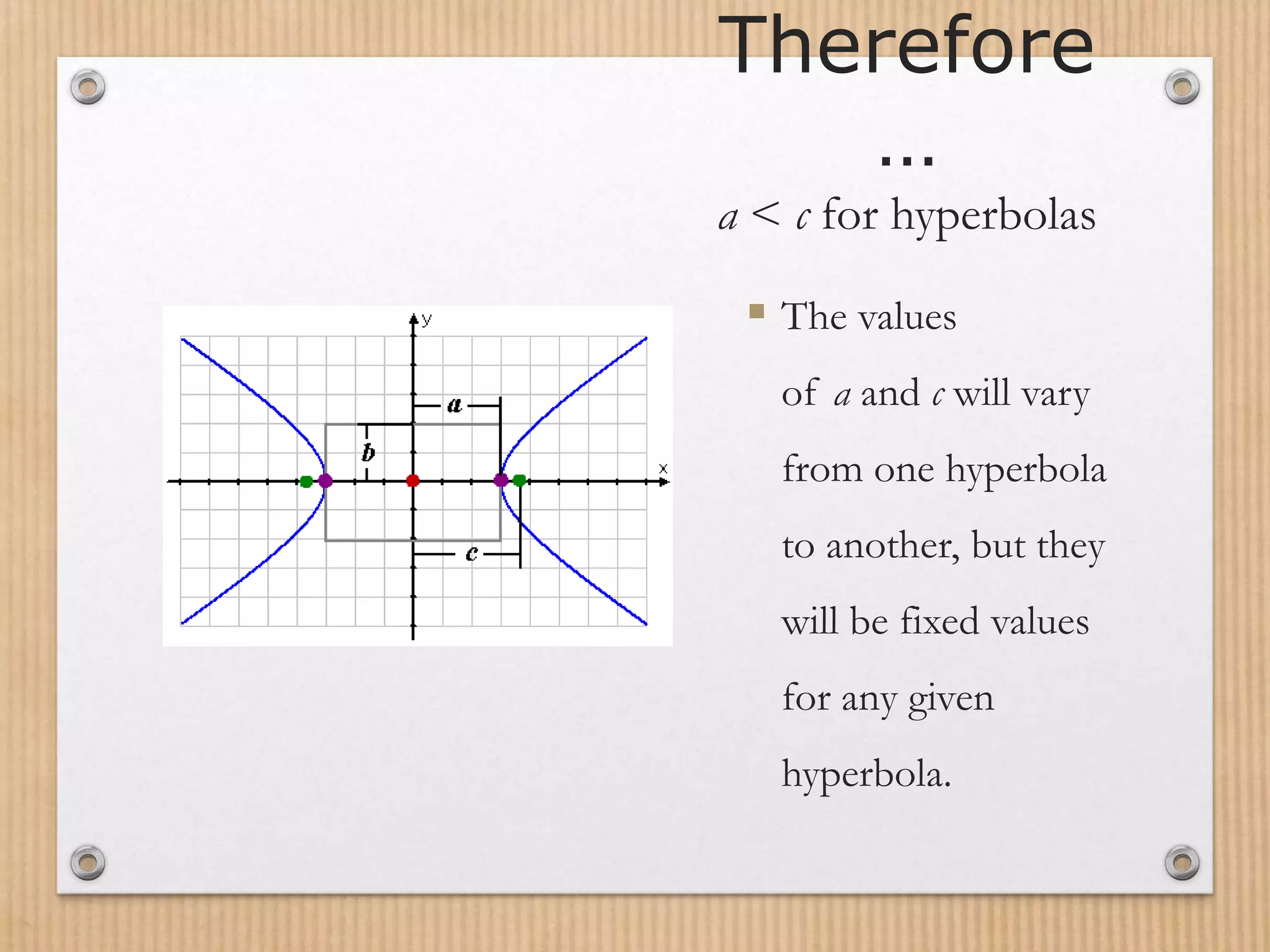
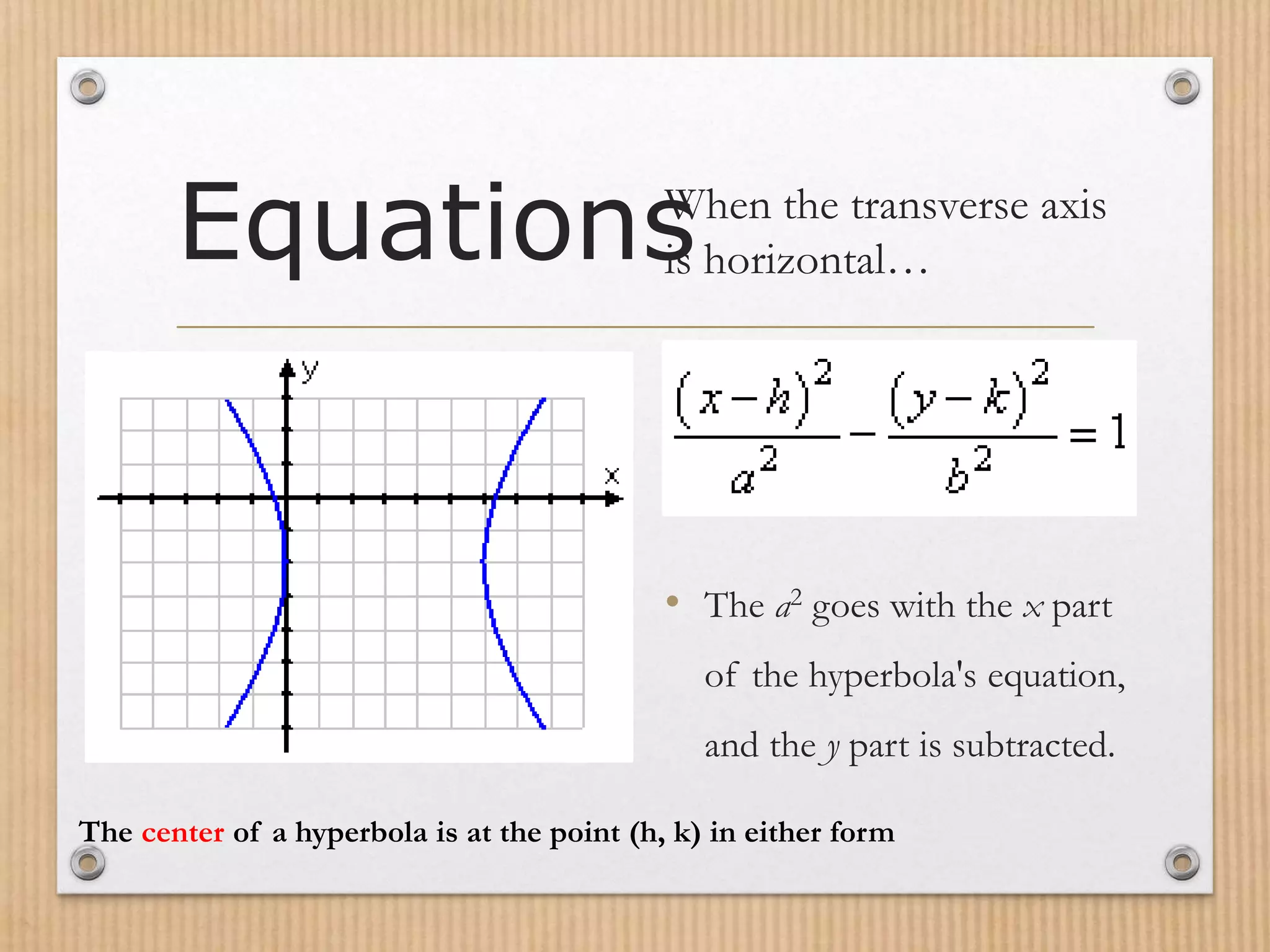
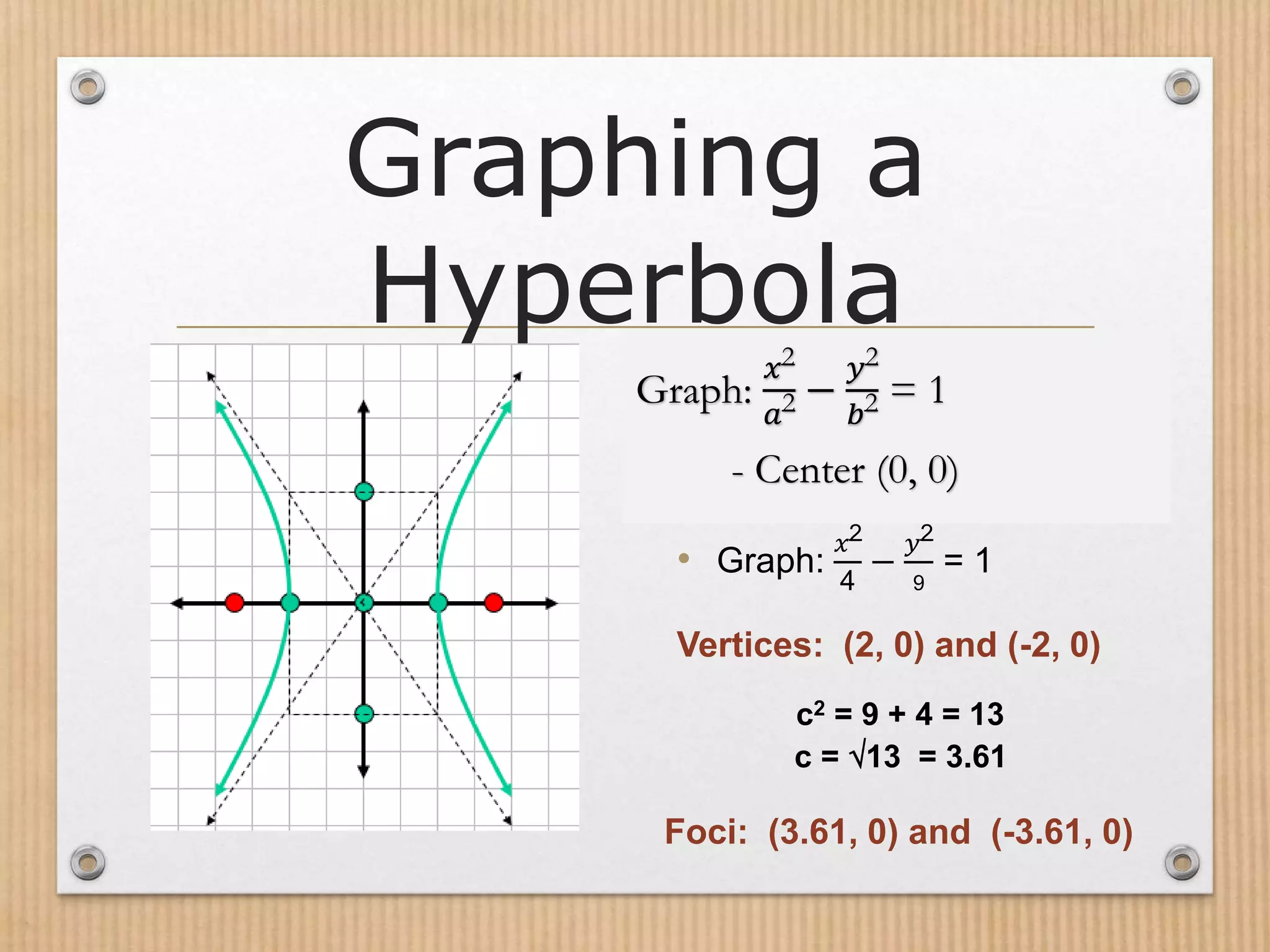
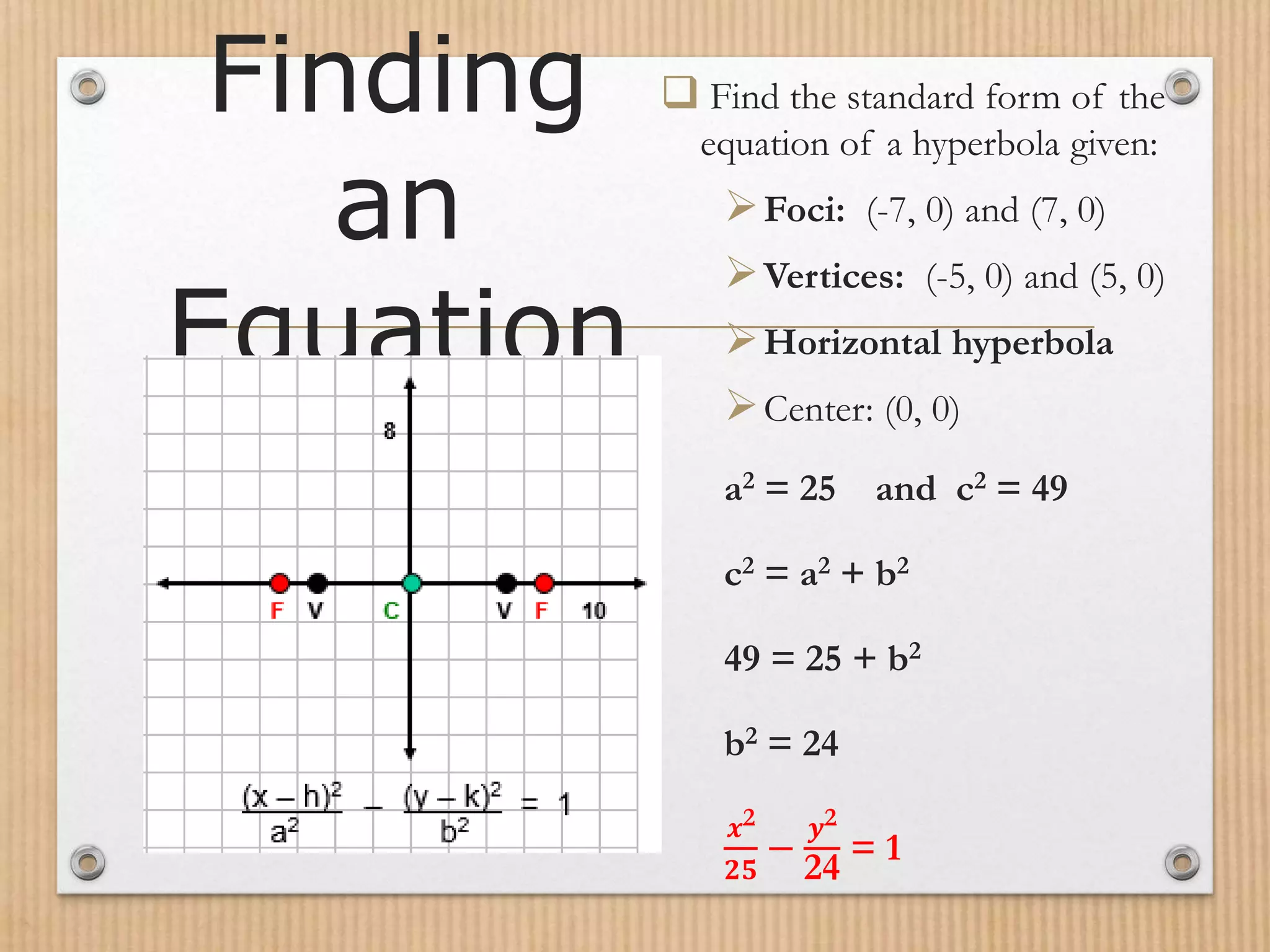
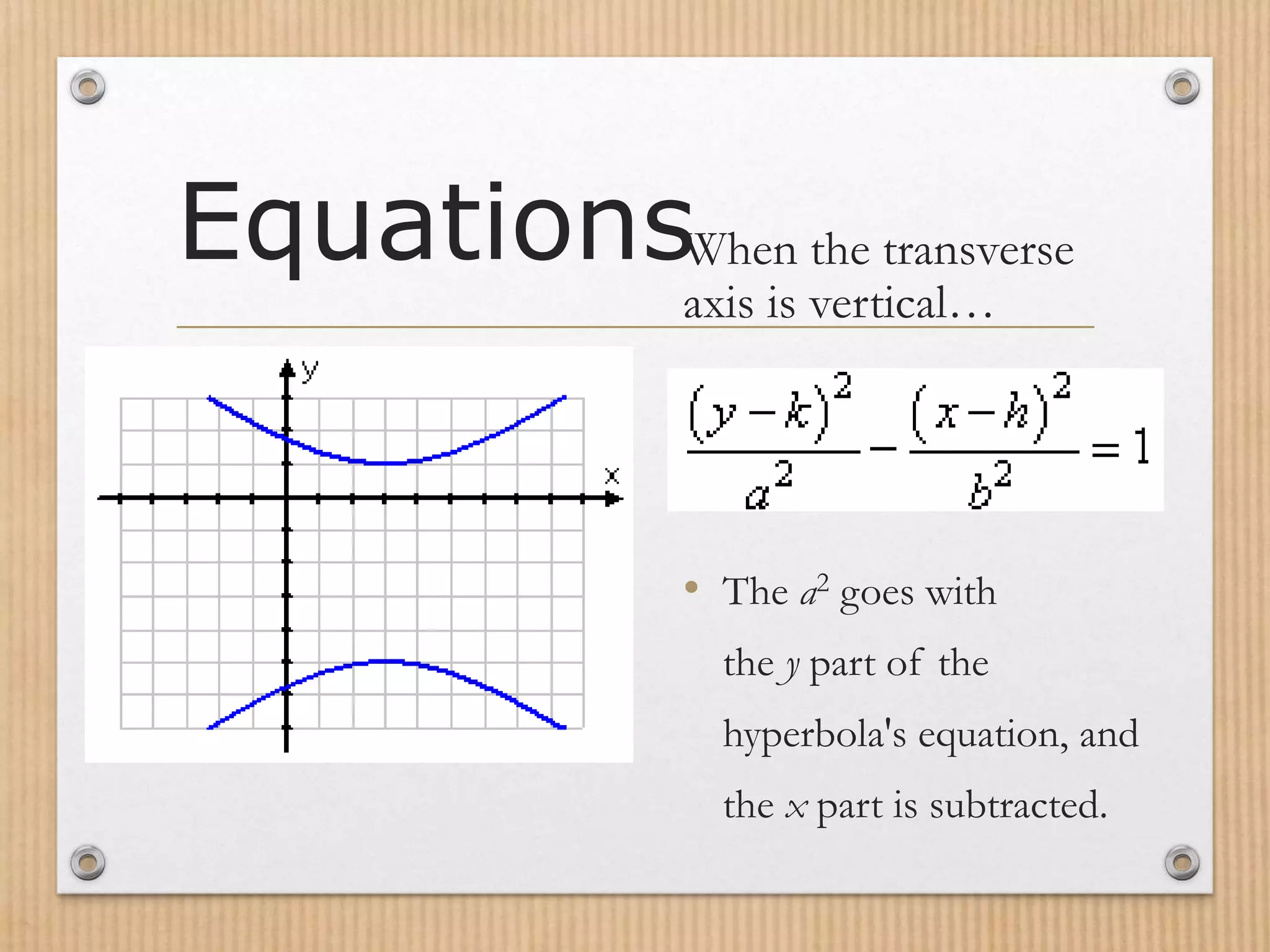
This document provides information about hyperbolas including: - Hyperbolas have two branches and two vertices, with the foci further from the center than the vertices. - The fundamental properties of a hyperbola include its center, vertices, foci, transverse axis, and the relationship between a, b, and c. - Hyperbolas can be graphed using their standard form equations, with the equation varying depending on the orientation of the transverse axis. 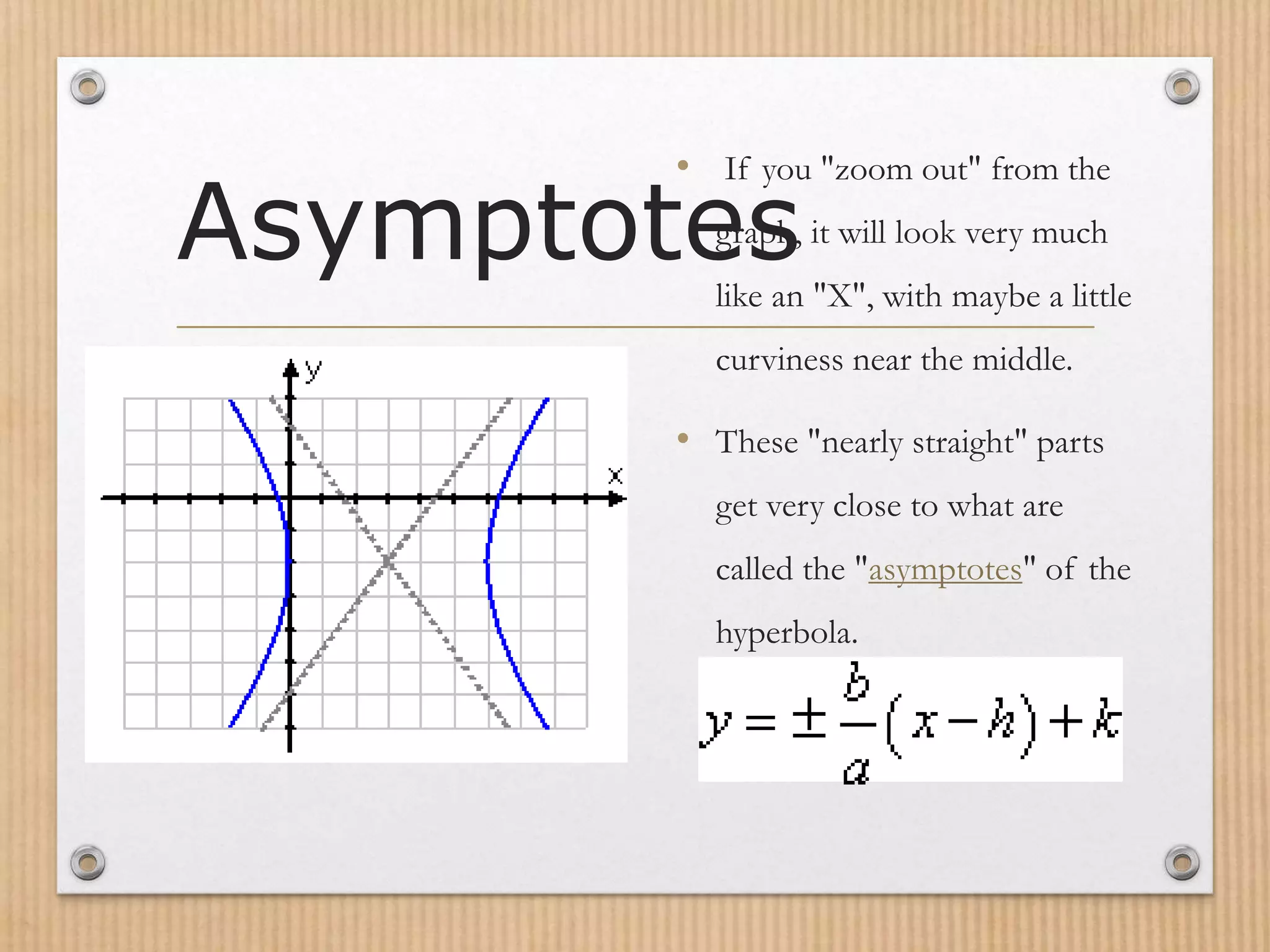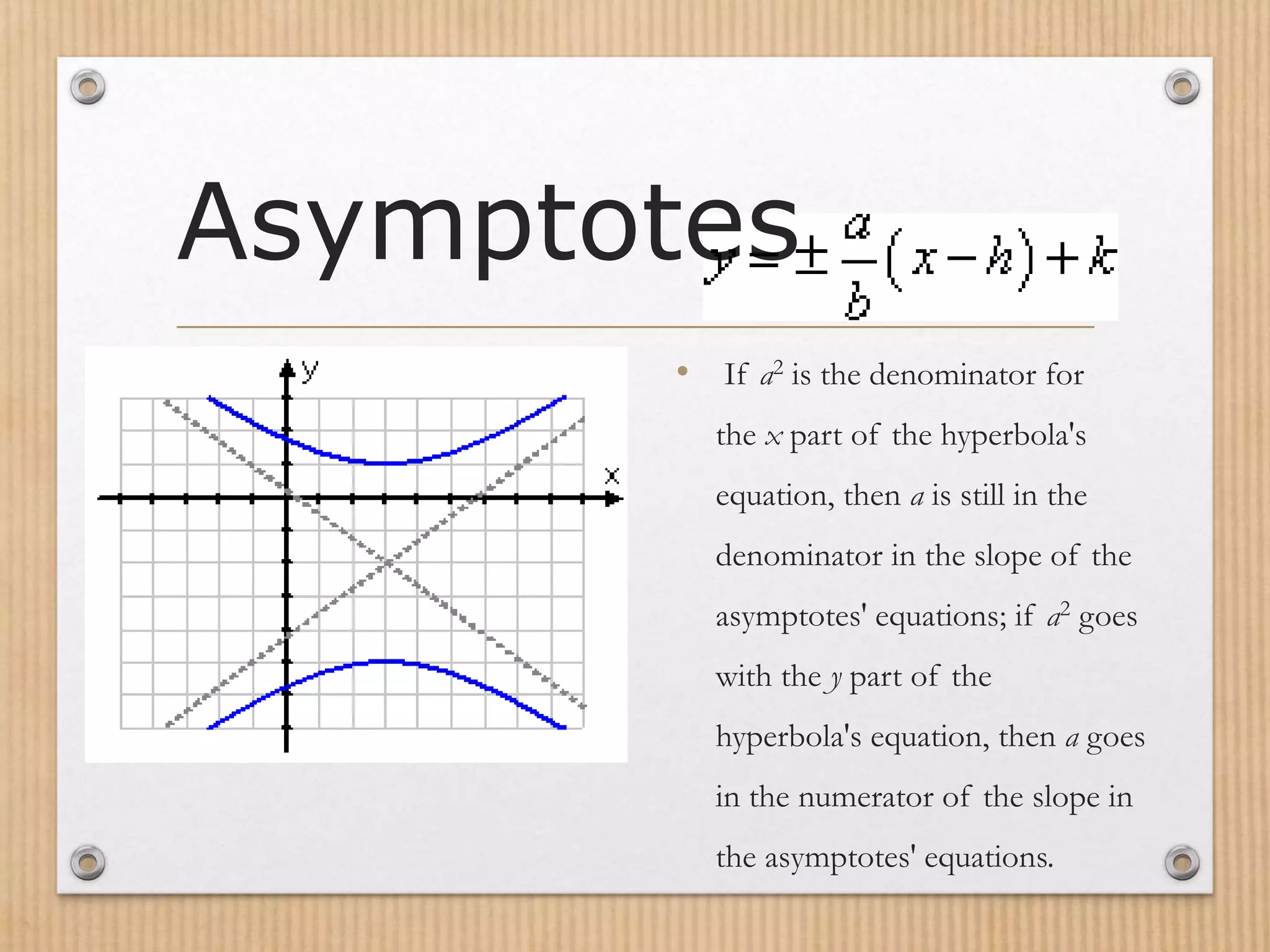- Asymptotes are straight lines that the branches of the hyperbola curve towards at increasing distance from the center. 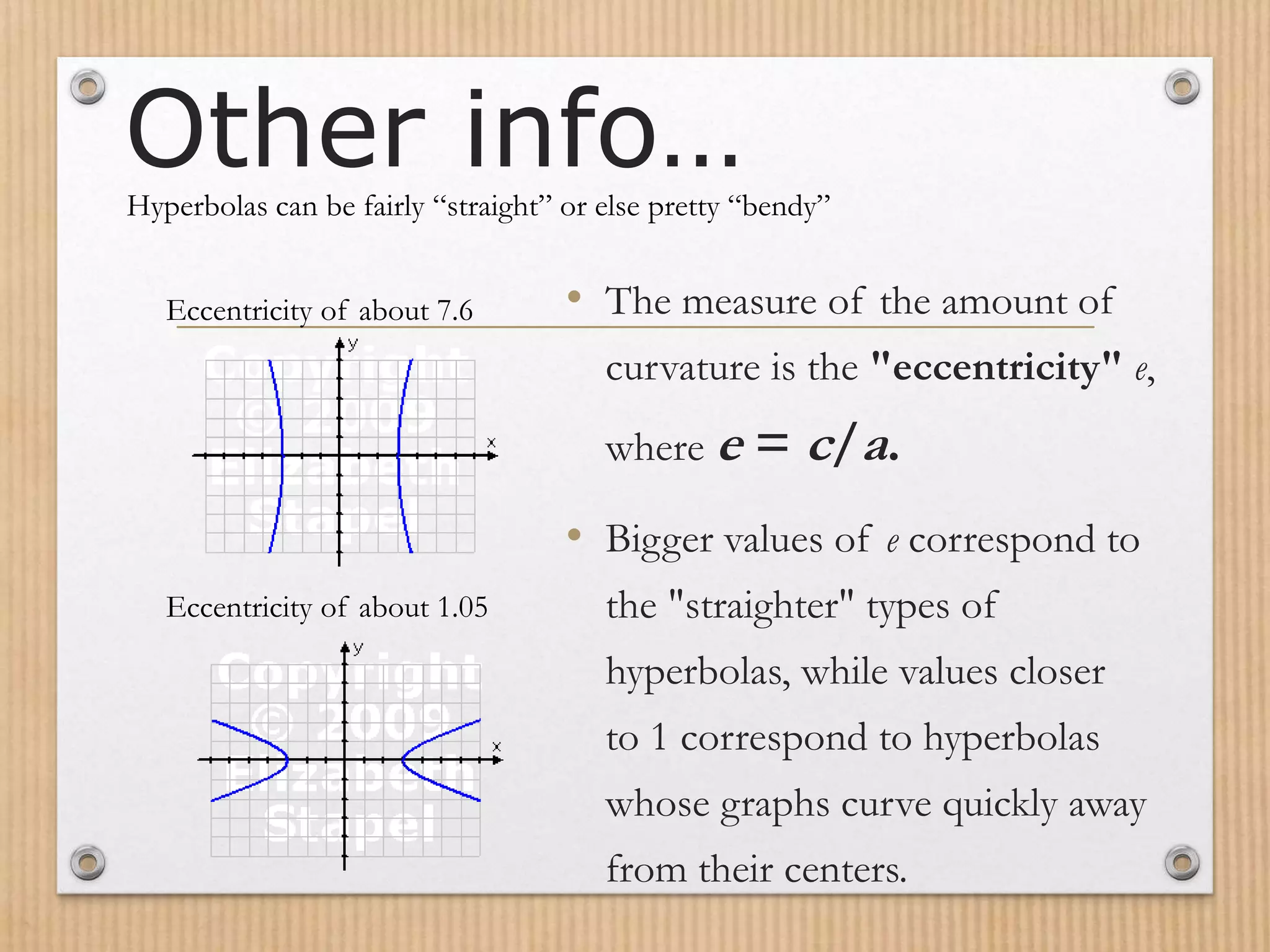- Properties like eccentricity describe the amount of curvature in hyperbolas.

1. HYPERBO
LAS
Discussants:
Table 3

2. Concept of a
Hyperbola
• A hyperbola looks sort of
like two mirrored parabolas,
with the two "halves" being
called "branches".
• Like an ellipse, a hyperbola
has two foci and two
vertices.
• Unlike an ellipse, the foci in
a hyperbola are further from
the hyperbola's center than
are its vertices.

3. For any Point…

4. Therefore
…
a < c for hyperbolas
 The values
of a and c will vary
from one hyperbola
to another, but they
will be fixed values
for any given
hyperbola.

5. Parts of a
Hyperbola
• “center” of the
hyperbola
• branch's “vertex”
• The "foci" of a
hyperbola are inside each
branch
• The line going from one
vertex, through the
center, and ending at the
other vertex is called the
“transverse” axis

6. (a + c) – (c – a) = 2a
This fixed-difference
property can used for
determining locations.
c2 = a2 + b2
Where c is the
distance from the
center to a focus
point.

7. The fundamental
box…
• The value of b gives the
"height" of the "fundamental
box" for the hyperbola
• The asymptotes pass through
the corners of a rectangle of
dimensions 2a by 2b, with its
center at (h, k)

8. EquationsWhen the transverse axis
is horizontal…
• The a2 goes with the x part
of the hyperbola's equation,
and the y part is subtracted.
The center of a hyperbola is at the point (h, k) in either form

9. EquationsWhen the transverse
axis is vertical…
• The a2 goes with
the y part of the
hyperbola's equation, and
the x part is subtracted.

10. Asymptotes
• If you "zoom out" from the
graph, it will look very much
like an "X", with maybe a little
curviness near the middle.
• These "nearly straight" parts
get very close to what are
called the "asymptotes" of the
hyperbola.

11. Asymptotes
• If a2 is the denominator for
the x part of the hyperbola's
equation, then a is still in the
denominator in the slope of the
asymptotes' equations; if a2 goes
with the y part of the
hyperbola's equation, then a goes
in the numerator of the slope in
the asymptotes' equations.

12. Graphing a
Hyperbola
• Graph:
𝑥2
4
−
𝑦2
9
= 1
Vertices: (2, 0) and (-2, 0)
c2 = 9 + 4 = 13
c = 13 = 3.61
Foci: (3.61, 0) and (-3.61, 0)
Graph:
𝑥2
𝑎2 −
𝑦2
𝑏2 = 1
- Center (0, 0)

13. Graphing a
Hyperbola
• Graph:
(𝑥+2)2
9 −
(𝑦−1)2
25 = 1
Vertices: (-5, 1) and (1, 1)
c2 = 9 + 25 = 34
c = 34 = 5.83
Foci: (-7.83, 1) and (3.83, 1)
Graph:
(𝑥−ℎ)2
𝑎2 −
(𝑦−k)2
𝑏2 = 1
- Center (-2, 1)

14. Finding
an
Equation
 Find the standard form of the
equation of a hyperbola given:
Foci: (-7, 0) and (7, 0)
Vertices: (-5, 0) and (5, 0)
Horizontal hyperbola
Center: (0, 0)
a2 = 25 and c2 = 49
c2 = a2 + b2
49 = 25 + b2
b2 = 24
𝒙2
𝟐𝟓
−
𝒚2
24
= 1

15. Sketching a
Hyperbola
• Sketch the
hyperbola whose
equation is…
4x2 – y2 = 16.
• Solution:

16. Other info…
• The measure of the amount of
curvature is the "eccentricity" e,
where e = c/a.
• Bigger values of e correspond to
the "straighter" types of
hyperbolas, while values closer
to 1 correspond to hyperbolas
whose graphs curve quickly away
from their centers.
Hyperbolas can be fairly “straight” or else pretty “bendy”
Eccentricity of about 7.6
Eccentricity of about 1.05

17. “Hyperbola”
• Was given its present name by Apollonius
who was the first to study the two branches
of the hyperbola.
• Euclid and Aristaeus wrote about the general
hyperbola but only studied one branch of it

18. Thankiiie
ee!!!
Twitter: @zelgandako
Instagram: @zelgandugh