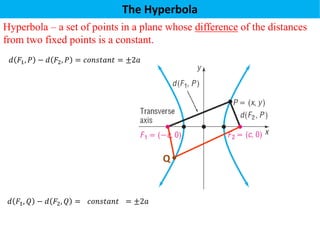
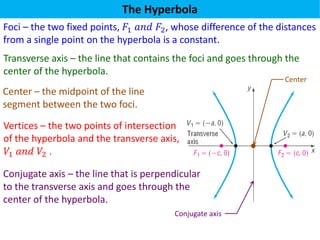
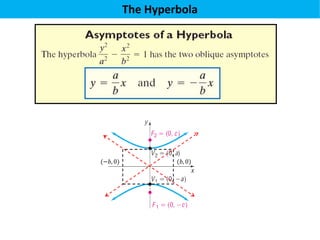
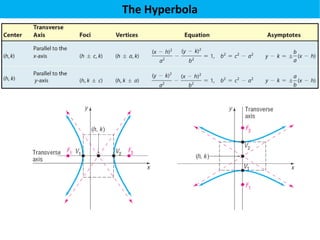
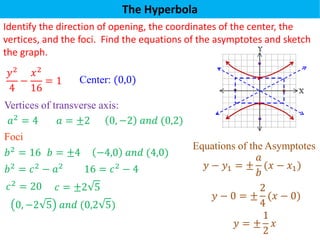
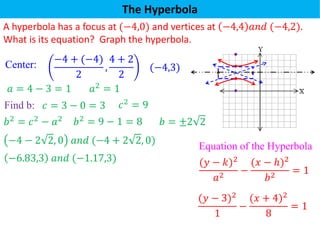
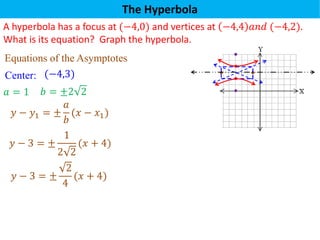
The document defines a hyperbola as a set of points where the difference between the distances from two fixed points (foci) is a constant. It provides details on key hyperbola elements including the transverse and conjugate axes, vertices, center, and foci. Examples are given demonstrating how to identify these elements from the equation of a hyperbola and sketch the graph. The last example solves for the center, vertices, foci and asymptote equations of a hyperbola given its equation.

1. Hyperbola – a set of points in a plane whose difference of the distances
from two fixed points is a constant.
The Hyperbola

2. The Hyperbola
Q
𝑑 𝐹1, 𝑄 − 𝑑 𝐹2, 𝑄 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 = ±2𝑎
Hyperbola – a set of points in a plane whose difference of the distances
from two fixed points is a constant.
𝑑 𝐹1, 𝑃 − 𝑑 𝐹2, 𝑃 = 𝑐𝑜𝑛𝑠𝑡𝑎𝑛𝑡 = ±2𝑎


3. The Hyperbola
Foci – the two fixed points, 𝐹1 𝑎𝑛𝑑 𝐹2, whose difference of the distances
from a single point on the hyperbola is a constant.
Transverse axis – the line that contains the foci and goes through the
center of the hyperbola.
Vertices – the two points of intersection
of the hyperbola and the transverse axis,
𝑉1 𝑎𝑛𝑑 𝑉2 .
Conjugate axis – the line that is perpendicular
to the transverse axis and goes through the
center of the hyperbola.
Conjugate axis
Center – the midpoint of the line
segment between the two foci.
Center


4. The Hyperbola

5. The Hyperbola

6. The Hyperbola

7. The Hyperbola
(−𝑏, 0) (𝑏, 0)

8. The Hyperbola

9. The Hyperbola
Identify the direction of opening, the coordinates of the center, the
vertices, and the foci. Find the equations of the asymptotes and sketch
the graph.
𝑥2
16
−
𝑦2
9
= 1
Vertices of transverse axis:
𝑎2 = 16
Center: (0,0)
Equations of the Asymptotes
Foci
𝑏2 = 9
𝑏2
= 𝑐2
− 𝑎2
𝑎 = ±4 −4,0 𝑎𝑛𝑑 (4,0)
𝑏 = ±3 0,3 𝑎𝑛𝑑 (0, −3)
9 = 𝑐2
− 16
𝑐2 = 25 𝑐 = ±5
−5,0 𝑎𝑛𝑑 (5,0)
 


 
𝑦 − 𝑦1 = ±
𝑏
𝑎
(𝑥 − 𝑥1)
𝑦 − 0 = ±
3
4
(𝑥 − 0)
𝑦 = ±
3
4
𝑥

10. The Hyperbola
𝑦2
4
−
𝑥2
16
= 1
Vertices of transverse axis:
𝑎2 = 4
Center: (0,0)
Equations of the Asymptotes
Foci
𝑏2 = 16
𝑏2
= 𝑐2
− 𝑎2
𝑎 = ±2 0, −2 𝑎𝑛𝑑 (0,2)
𝑏 = ±4 −4,0 𝑎𝑛𝑑 (4,0)
16 = 𝑐2
− 4
𝑐2 = 20 𝑐 = ±2 5
0, −2 5 𝑎𝑛𝑑 (0,2 5)


 


𝑦 − 𝑦1 = ±
𝑎
𝑏
(𝑥 − 𝑥1)
𝑦 − 0 = ±
2
4
(𝑥 − 0)
𝑦 = ±
1
2
𝑥
Identify the direction of opening, the coordinates of the center, the
vertices, and the foci. Find the equations of the asymptotes and sketch
the graph.

11. The Hyperbola
(𝑦 − 𝑘)2
𝑎2
−
(𝑥 − ℎ)2
𝑏2
= 1
Find b:
𝑎2 = 1
Center:
𝑏2 = 9 − 1 = 8
𝑏2 = 𝑐2 − 𝑎2
𝑎 = 4 − 3 = 1
Equation of the Hyperbola
𝑏 = ±2 2
−4 − 2 2, 0 𝑎𝑛𝑑 (−4 + 2 2, 0)
𝑐2 = 9
𝑐 = 3 − 0 = 3
−6.83,3 𝑎𝑛𝑑 (−1.17,3)


 


A hyperbola has a focus at (−4,0) and vertices at −4,4 𝑎𝑛𝑑 (−4,2).
What is its equation? Graph the hyperbola.
−4 + (−4)
2
,
4 + 2
2
(−4,3)
(𝑦 − 3)2
1
−
(𝑥 + 4)2
8
= 1

12. The Hyperbola
Center:
Equations of the Asymptotes
𝑎 = 1 𝑏 = ±2 2


 


𝑦 − 𝑦1 = ±
𝑎
𝑏
(𝑥 − 𝑥1)
𝑦 − 3 = ±
1
2 2
(𝑥 + 4)
A hyperbola has a focus at (−4,0) and vertices at −4,4 𝑎𝑛𝑑 (−4,2).
What is its equation? Graph the hyperbola.
(−4,3)
𝑦 − 3 = ±
2
4
(𝑥 + 4)

13. The Hyperbola
Find the center, the vertices of the transverse axis, the foci and the
equations of the asymptotes using the following equation of a hyperbola.
𝑦2
− 4𝑥2
− 72𝑥 + 10𝑦 − 399 = 0
𝑦2 + 10𝑦 − 4(𝑥2 + 18𝑥) = 399
10
2
= 5 52 = 25
18
2
= 9 92 = 81
𝑦2 + 10𝑦 + 25 − 4(𝑥2+18𝑥 + 81) = 399 + 25 − 324
(𝑦 + 5)2−4(𝑥 + 9)2= 100
(𝑦 + 5)2
100
−
4(𝑥 + 9)2
100
= 1
(𝑦 + 5)2
100
−
(𝑥 + 9)2
25
= 1
𝑦2 + 10𝑦 − 4𝑥2 − 72𝑥 = 399
Opening up/down

14. The Hyperbola
Find the center, the vertices of the transverse axis, the foci and the
equations of the asymptotes using the following equation of a hyperbola.
𝑦2
− 4𝑥2
− 72𝑥 + 10𝑦 − 399 = 0
(𝑦 + 5)2
100
−
(𝑥 + 9)2
25
= 1
Center: (−9, −5)
Vertices:
𝑎2 = 100 𝑎 = 10
−9, −5 − 10 𝑎𝑛𝑑 (−9, −5 + 10)
−9, −15 𝑎𝑛𝑑 (−9,5)
Foci:
25 = 𝑐2 − 100
𝑏2 = 𝑐2 − 𝑎2
−9, −5 − 5 5 𝑎𝑛𝑑 (−9, −5 + 5 5)
𝑐 = 125 = 5 5
−9, −16.18 𝑎𝑛𝑑 (−9,6.18)
𝑐2 = 125

15. The Hyperbola
Find the center, the vertices of the transverse axis, the foci and the
equations of the asymptotes using the following equation of a hyperbola.
𝑦2
− 4𝑥2
− 72𝑥 + 10𝑦 − 399 = 0
(𝑦 + 5)2
100
−
(𝑥 + 9)2
25
= 1
Center: (−9, −5)
𝑎 = 10
Equations of the Asymptotes
𝑦 − 𝑦1 = ±
𝑎
𝑏
(𝑥 − 𝑥1)
𝑏 = 5
𝑦 − (−5) = ±
10
5
(𝑥 − (−9))
𝑦 + 5 = ±2 (𝑥 + 9)